概要
物質を混合したときに生じるエンタルピー変化を混合熱、もしくは混合エンタルピーといいます。
混合する物質によってはプロセスの温度が大きく変化しうるため、気を付けなければならない要素の1つです。
混合熱の実測値や文献値があれば、その値を使用するのが最も良いですが、ないこともあるでしょう。
この記事では混合熱の理論的な位置付けや推算方法について解説します。
混合エンタルピーの理論
混合エンタルピーの理論について考えてみましょう。
理想混合物
まず理想混合物の混合エンタルピーΔhidについて考えます。
ギブス自由エネルギーの定義から、
$$Δh^{id}=Δg^{id}+TΔs^{id}・・・(1)$$
(1)式が成り立ちます。
よって、混合エントロピーΔsidと混合ギブス自由エネルギーΔgidから混合エンタルピーΔhidを計算できます。
これら2つの導出は以下の記事で解説していますので、本記事では省略します。
-

【エントロピー】をわかりやすく解説:エネルギー変換の不可逆性を示す指標
仕事と熱はどちらもエネルギーではありますが、エネルギーとしての質の違いが存在しお互いに自由に変換することはできません。エネルギー変換の不可逆性に注目し、エネルギー変化が起こる方向を定量的に扱うために導入された状態量をエントロピーといいます。
続きを見る
-

【ギブス自由エネルギー】をわかりやすく解説:閉鎖系の自発変化の方向や平衡状態を表現
実際のプロセスでは系に外部からエネルギーを加える、あるいは外部へとエネルギーを放出する操作を行なうことがほとんどです。そのため、外部からのエネルギーの出入りが可能な閉鎖系へと理論を拡張する必要があります。このときに役に立つのが自由エネルギーの概念です。
続きを見る
2成分A,Bが混合する場合、
$$Δs^{id}=-R(n_{A}{\rm{ln}}x_{A}+n_{B}{\rm{ln}}x_{B})・・・(2)$$
$$Δg^{id}=RT(n_{A}{\rm{ln}}x_{A}+n_{B}{\rm{ln}}x_{B})・・・(3)$$
(2)、(3)式となります。
したがって、
$$Δh^{id}=RT(n_{A}{\rm{ln}}x_{A}+n_{B}{\rm{ln}}x_{B})-RT(n_{A}{\rm{ln}}x_{A}+n_{B}{\rm{ln}}x_{B})=0・・・(4)$$
(4)式のように理想混合物の混合エンタルピーはΔhid=0となります。
実在混合物
続いて、実在混合物の混合エンタルピーを考えます。
実在混合物の状態量は過剰量を使用すると簡単に表すことができます。
過剰量は実在混合物と理想混合物のずれを表わし、詳細については以下の記事で解説しています。
-

【過剰量】を解説:実在混合物と理想混合物の状態量の差
過剰量は実在混合物と理想混合物の状態量の差として定義されています。気液平衡を計算するための活量係数モデルでは、過剰量が大いに関係しており重要な概念です。本記事では過剰量について解説しています。
続きを見る
実在混合物の混合エンタルピー変化Δhは、
$$Δh=Δh^{id}+h^{E}・・・(5)$$
hE:過剰エンタルピー
(5)式で表されます。
Δhid=0であるため、Δh=hEとなります。
したがって、実在混合物の混合エンタルピー変化Δhは過剰エンタルピーhEそのものであることがわかります。
過剰エンタルピー
過剰エンタルピーhEを算出できれば実在混合物の混合エンタルピー変化Δhがわかります。
ギブスーヘルムホルツの式を過剰量に対して適用すると、
$$\Bigl(\frac{∂g^{E}/T}{∂T}\Bigr)_{p}=-\frac{Δh^{E}}{T^{2}}・・・(6)$$
(6)式となります。
また、過剰ギブス自由エネルギーgEは、
$$g^{E}=RT\sum x_{i}{\rm{ln}}γ_{i}・・・(7)$$
(7)式で定義されています。
(7)式を(6)式に代入して整理すると、
$$h^{E}=-RT^{2}\sum x_{i}\frac{∂{\rm{ln}}γ_{i}}{∂T}・・・(8)$$
(8)式となります。
したがって、過剰エンタルピーhEは活量係数γから算出することができます。
活量係数の決定における問題
過剰エンタルピーを算出するためには実測データから活量係数を決定する必要があります。
ここで問題なのが、どのような実測データを使用して活量係数をフィッティングするかです。
活量係数は一般に、気液平衡を計算する目的で使用されることが多く、気液平衡データ(以下、VLEデータ)を使用してフィッティングすることが多いです。
VLEデータを使用して決定された活量係数を使用すれば、気液平衡計算の精度は当然良くなります。
一方で同じ活量係数で過剰エンタルピーhEを計算すると精度が悪くなることが多いです。
ここではエタノール-水の2成分系で具体例をみてみます。
VLEデータでフィッティング
まずVLEデータを使用して活量係数をフィッティングした例を見てみましょう。
活量係数モデルはNRTLを使用します。

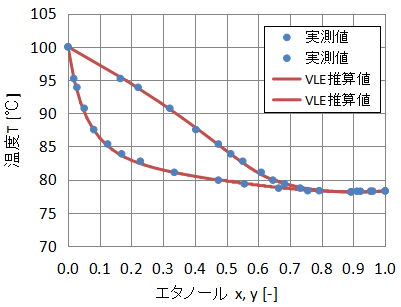
VLEデータを使用してフィッティングしたので、実測値とNRTLモデルの推算値がよく一致していますね。
一方で、同じ活量係数を使用して過剰エンタルピーhEを算出した結果を示します。
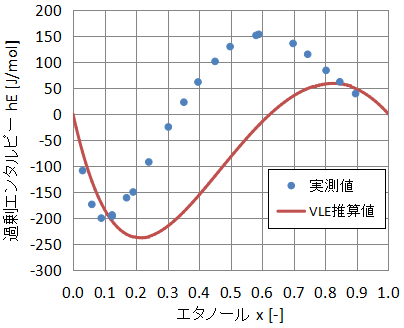
実測値と推算値でずれており、VLEデータでフィッティングした活量係数では混合熱をうまく表現できないことがわかります。
混合熱データでフィッティング
次に、混合熱の実測データを使用して活量係数をフィッティングしてみます。
過剰エンタルピーの結果を下図に示します。
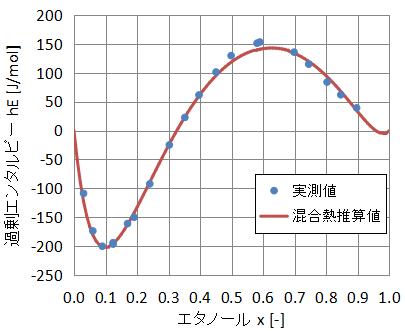
実測値と推算値が比較的よく一致していることがわかります。
一方で、同じ活量係数を使用してNRTLモデルで気液平衡を計算した結果を示します。
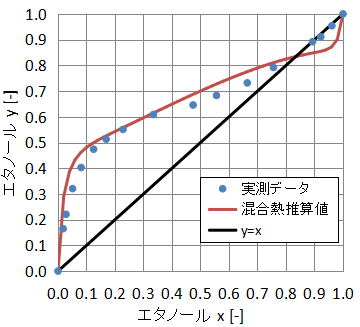
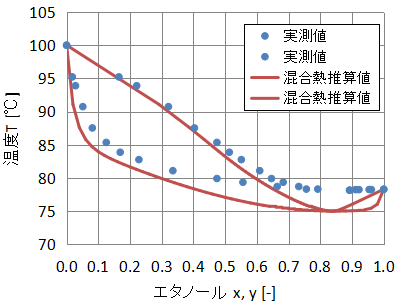
エタノール-水系の共沸点温度が大きくずれていることがわかります。
したがって、混合熱から決定した活用係数では気液平衡をうまく表現できないということになります。
VLEデータ:混合熱データ=1:1でフィッティング
最後に、VLEデータと混合熱データを両方使用し、1:1の重みづけでフィッティングしたときの結果を見てみましょう。
xy線図とTxy線図の結果を以下に示します。

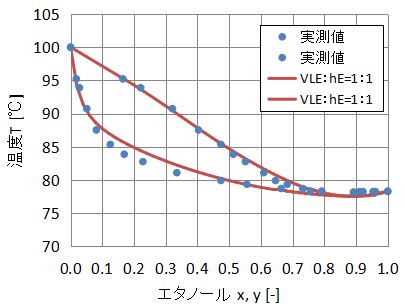
比較的実測データに近い傾向を示していますが、VLEデータのみから推算した結果に比べれば精度は悪いですね。
続いて過剰エンタルピーの結果を下図に示します。
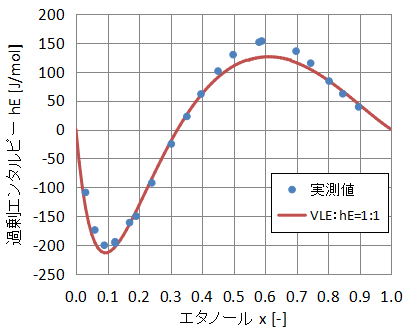
こちらも比較的実測データに近い傾向を示していますが、一部の区間では誤差が大きくなっています。
以上の結果から、両方のデータでフィッティングした場合は、気液平衡・過剰エンタルピーそれぞれの結果がそこそこの精度で表現できるようです。
混合熱の扱い
結局、活量係数をどのようなデータからフィッティングすべきかについては、明確な結論はありません。
ただ、装置設計の観点から考えると、気液平衡を蔑ろにするわけにはいきませんので、扱う系によって混合熱の扱いを変えるのがよいでしょう。
①混合熱を無視する
最もシンプルな対応が混合熱を無視することです。
活量係数が1に近く非理想性があまり高くない系においては、混合熱もあまり大きくないでしょう。
混合熱によるプロセスの温度変化がわずかである場合は、無視しても装置設計に影響することはほとんどないはずです。
あるいは熱交換器や蒸留塔の設計においては、外部との熱のやり取りによる交換熱量が圧倒的に大きいため、混合熱を無視できることが多いです。
したがって、活量係数は気液平衡(VLE)のみでフィッティングするのがよいでしょう。
②フィッティングの重みづけを変える
本記事では気液平衡と混合熱データを1:1の重みづけでフィッティングしましたが、重みづけを変えることもできます。
"気液平衡は精度良く推算したいけど、混合熱の精度はそこそこで良い"、という場合は気液平衡の重みづけを増やすことで望ましいフィッティングができるかもしれません。
試行錯誤の話になるので、仕事の締切・納期との相談にもなります。
③モデル・設定・ファイルを使い分ける
混合熱を計算したい箇所がある場合は、モデルや設定、計算ファイルを使い分けることも考えられます。
気液平衡はVLEデータでフィッティングした活量係数で、過剰エンタルピーは混合熱データでフィッティングした活量係数で計算するのが最も望ましい使い分けでしょう。
ただし、活量係数を使い分けできるかどうかは使用している計算環境やシミュレータ次第でしょう。
商用のシミュレータを使用している場合は、必ずしもユーザーが望む設定ができないこともあります。ユーザーがシミュレータの式を修正する機能が付いている場合もありますので、サポートに相談してみましょう。
④文献値等から温度変化を直接計算する
マテバラや装置設計を行なううえでは、過剰エンタルピーの値はどうでもよく、混合熱によってどのくらい系が温度変化するのかがわかればよいです。
そのため、活量係数による過剰エンタルピーの計算はせず、文献値等から混合熱による交換熱量を直接求め、系の温度を別途修正すれば実用上は問題ないはずです。
この手法は、気液平衡を電解質モデルで計算せざるをえないような、強酸・強塩基の混合に向いているのではと思います。
電解質モデルの活量係数を、過剰エンタルピーも合うようにフィッティングするのは大変ですからね。
おわりに
混合熱について解説しました。
気液平衡と過剰エンタルピーを両方完璧に合わせるのは難しく、その系によって混合熱の扱いを変える必要があります。


