概要
仕事と熱はどちらもエネルギーではありますが、エネルギーとしての質の違いが存在します。
仕事は熱に100%変換できますが、熱は40%程度しか仕事に変換できず、同じエネルギーでも自由に変換することができません。
このようなエネルギー変換の不可逆性に注目し、エネルギー変化が起こる方向を定量的に扱うために導入された状態量をエントロピーといいます。
エントロピーはSという記号を使用し、以下の式で定義されています。
$$S_{2}-S_{1}=\int_{1}^{2}\frac{δQ}{T}・・・(1)$$
S1,S2:状態1,2におけるエントロピー[J/K]
Q:熱量[J]、T:温度[K]
微分形で表すと、
$$dS=\frac{δQ}{T}・・・(2)$$
(2)式となります。
この記事では、エントロピーに関する内容をいくつか紹介します。
エントロピーの導入背景
もともとエントロピーはカルノーサイクルを考える過程で導入されました。
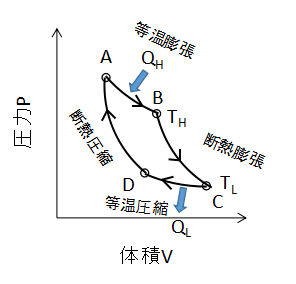
上図に理想気体のカルノーサイクルのPV線図を示します。
カルノーサイクルは等温変化と断熱変化の組み合わせにより、熱を仕事へと変換するサイクルです。
ただし、前述したように熱を100%仕事へと変換することはできず、熱効率ηと呼ばれるエネルギーの変換効率が(3)式で表されます。
$$η=1-\frac{Q_{L}}{Q_{H}}・・・(3)$$
QL:低熱源に捨てる熱量[J]、QH:高熱源から供給される熱量[J]
ここで、カルノーサイクルの2つの等温変化に注目します。
まずA⇒Bの等温変化の仕事について考えます。
仕事の定義から、
$$W_{AB}=\int_{V_{A}}^{V_{B}}PdV・・・(4)$$
(4)式となります。
次に、理想気体の状態方程式から、
$$PV=nRT・・・(5)$$
P:気体の圧力[Pa]、V:気体の体積[m3]、n:気体のモル量[-]
R:気体定数[J/(mol・K)]、気体の温度[K]
(5)式が成り立ちます。(5)式を(4)式に代入すると、
$$W_{AB}=\int_{V_{A}}^{V_{B}}\frac{nRT}{V}dV・・・(6)$$
(6)式となります。
ここで、等温変化なので温度Tは一定温度THとして扱えます。そのため、(6)式を体積Vについて積分することができます。
$$W_{AB}=nRT_{H}{\rm{ln}}\frac{V_{B}}{V_{A}}・・・(7)$$
(7)式がA⇒Bの等温変化での仕事を表わす式となります。
また、温度T一定であるため内部エネルギー変化ΔU=0となります。
したがって、熱力学の第一法則から、
$$Q_{H}=W_{AB}=nRT_{H}{\rm{ln}}\frac{V_{B}}{V_{A}}・・・(8)$$
熱量QHは(8)式となります。
同様に、C⇒Dの等温変化についても式を立てます。
ほぼ同じ導出なので省略しますが、熱量QLは、
$$Q_{L}=W_{CD}=nRT_{L}{\rm{ln}}\frac{V_{C}}{V_{D}}・・・(9)$$
(9)式となります。
次にB⇒Cの断熱変化について考えます。
ポアソンの式から断熱変化では、
$$T_{H}{V_{B}}^{γ-1}=T_{L}{V_{C}}^{γ-1}・・・(10)$$
γ:比熱容量の比[-]
(10)式が成り立ちます。
同様にD⇒Aの断熱変化では、
$$T_{H}{V_{A}}^{γ-1}=T_{L}{V_{D}}^{γ-1}・・・(11)$$
(11)式が成り立ちます。
(10)式÷(11)式とすることで、
$$\frac{V_{B}}{V_{A}}=\frac{V_{C}}{V_{D}}・・・(12)$$
(12)式となります。
(12)式を利用しつつ、(9)式÷(8)式とすると、
$$\frac{Q_{L}}{Q_{H}}=\frac{T_{L}}{T_{H}}・・・(13)$$
(13)式となります。
(13)式を変形し、
$$\frac{Q_{L}}{T_{L}}-\frac{Q_{H}}{T_{H}}=0・・・(14)$$
(14)式の形にします。
ここで、状態量について考えます。
状態量とは系の状態を決めれば一義的に値が決まるものです。
サイクルが一巡して元の点に戻ったときは、状態量であるP、V、Tなどの変化量はゼロとなります。
熱量Qについては、
$$ΔQ=Q_{H}-Q_{L}>0・・・(15)$$
(15)式となるので明らかに状態量ではないです。
ところが、熱量Qを温度Tで割った(14)式は、サイクルが一巡すると値がゼロとなっており、状態量の条件を満たしています。
このような知見から、新たにエントロピーS=Q/Tという状態量の導入につながったと言われています。
理想気体のエントロピー変化
理想気体のエントロピーがどのように変化するか考えてみましょう。
まず、熱力学の第一法則は(16)式で表されます。
$$δQ=dU+PdV・・・(16)$$
(16)式とエントロピーの定義式(2)式からδQを消去すると、
$$TdS=dU+PdV・・・(17)$$
(17)式となります。
次に、理想気体であることから、
$$PV=nRT・・・(18)$$
$$dU=nC_{V}dT・・・(19)$$
CV:定容比熱
(18)、(19)式が成り立ちます。これらの式を(17)式に代入すると、
$$dS=nC_{V}\frac{dT}{T}+nR\frac{dV}{V}・・・(20)$$
(20)式となります。
状態1から状態2へと変化する場合に、(20)式を積分すると、
$$\begin{align}ΔS&=nC_{V}\int_{T_{1}}^{T_{2}}\frac{dT}{T}+nR\int_{V_{1}}^{V_{2}}\frac{dV}{V}\\&=nC_{V}{\rm{ln}}\frac{T_{2}}{T_{1}}+nR{\rm{ln}}\frac{V_{2}}{V_{1}}・・・(21)\end{align}$$
(21)式となります。
仮に等温変化dT=0であれば、(21)式は
$$ΔS=nR{\rm{ln}}\frac{V_{2}}{V_{1}}・・・(22)$$
(22)式となります。
エントロピー増大の法則
ある孤立系に不可逆変化が起こった場合、エントロピーは必ず増大します。
これをエントロピー増大の法則、あるいは熱力学第二法則といいます。
以下にエントロピーが増大する例をいくつか示します。
拡散のエントロピー変化
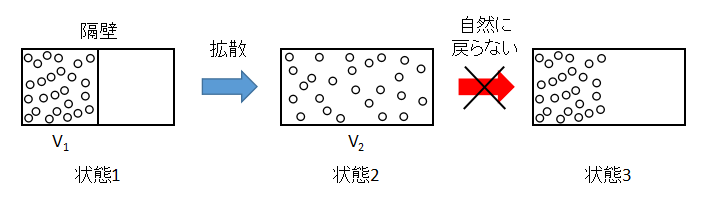
上図のような容器内の理想気体の拡散を考えます。
状態1から隔壁を取り除くと、気体は容器全体へと拡散し状態2となります。
一方で、状態2から状態3へと気体が左側へ自然に戻ることはないでしょう。
このような状態1から状態2への変化を不可逆変化といいます。
不可逆過程では経路を特定できないため、途中の過程を計算することはできません。
しかしエントロピーは状態量なので、状態1,2のエントロピー変化は準静的過程を考えることで計算できます。
仮に状態1から状態2まで理想気体の等温変化で変化したとすれば、エントロピー変化ΔS[J/K]は、
$$ΔS=nR{\rm{ln}}\frac{V_{2}}{V_{1}}・・・(22)$$
前述した(22)式のようになります。
状態1の体積V1と状態2の体積V2を比較すると、明らかにV2>V1ですので、(22)式はΔS>0となりエントロピー増大の法則を満たします。
混合のエントロピー変化
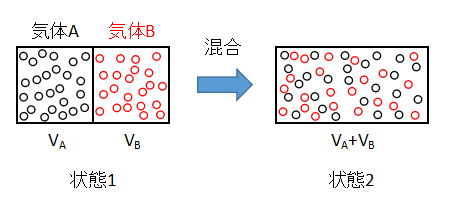
上図のような2種類の理想気体の混合を考えます。
隔壁で仕切られた容器内に2種類の気体を封入した状態を1とします。
隔壁を取り除くと、気体Aと気体Bは不可逆的に混合し、最終的には均一な状態2となります。
理想気体なので混合の過程で熱は発生せず、準静的過程が成り立ちます。
そのため混合によるエントロピー変化は、2種類の気体の拡散によるエントロピー変化を足し合わせたものと等しくなります。
前述した(22)式を参考に、混合のエントロピー変化ΔS[J/K]は、
$$ΔS=n_{A}R{\rm{ln}}\frac{V_{A}+V_{B}}{V_{A}}+n_{B}R{\rm{ln}}\frac{V_{A}+V_{B}}{V_{B}}・・・(23)$$
nA、nB:気体A,Bのモル数[-]
VA、VB:気体A,Bの体積[m3]
となります。
理想気体なので混合前後で圧力と温度は変わりませんから、PV=nRTより、
$$\frac{V_{A}}{V_{A}+V_{B}}=\frac{n_{A}}{n_{A}+n_{B}}=x_{A}・・・(24)$$
$$\frac{V_{B}}{V_{A}+V_{B}}=\frac{n_{B}}{n_{A}+n_{B}}=x_{B}・・・(25)$$
xA、xB:気体A,Bのモル分率[-]
(24)、(25)式となります。
これらの式を(23)式に代入すると、
$$ΔS=-n_{A}R{\rm{ln}}x_{A}-n_{B}R{\rm{ln}}x_{B}・・・(26)$$
(26)式となります。
モル分率xA、xBは0~1の値を示すため、(26)式はΔS>0となりエントロピー増大の法則を満たします。
相変化のエントロピー変化
例として、物質1molが蒸発するときのエントロピー変化ΔS[J/(mol・K)]を考えます。
蒸発に必要な熱量は蒸発熱ΔHV[J/mol]ですから、蒸発時のエントロピー変化は(2)式より、
$$ΔS=\frac{ΔH_{V}}{T}・・・(27)$$
T:相変化時の温度[K]
(27)式となります。
蒸発熱ΔHVも温度Tも正の値ですから、(24)式もΔS>0となりエントロピー増大の法則を満たします。
ちなみに、1atmにおける蒸発モルエントロピーΔSの値が80~88J/(mol・K)の値を示す法則を、トルートンの規則といいます。
この規則は、気体が理想気体だとすれば理由を簡単に説明できます。
液体が気体となる蒸発前後の体積変化でエントロピー変化を表わすと、(22)式を参考に、
$$ΔS=nR{\rm{ln}}\frac{V_{vapor}}{V_{liquid}}・・・(28)$$
(28)式となります。
理想気体の体積は1atmで22.4L一定となり、一方で液体の体積は気体に対して無視できるほど小さいです。
したがって、気体と液体の体積の比Vvapor/Vliquidは物質の種類によらずほぼ一定値を示し、ΔSも一定値となるということです。
ただし、水やエタノールのような水素結合を作る物質は他の物質よりも蒸発熱が大きくなる傾向にあるため、トルートンの規則は当てはまりません。
反応のエントロピー変化
一般に、標準状態における反応前後のエントロピー変化を計算することが多いでしょう。
これを標準反応エントロピーΔS0といいます。
例として、水の生成反応の標準反応エントロピーを求めてみましょう。
$$H_{2}+\frac{1}{2}O_{2}→H_{2}O(l)・・・(29)$$
水の生成反応は(29)式で表されます。
標準反応エントロピーは、反応前後の物質の標準エントロピーから算出できます。
標準エントロピーS0は基本的に文献を参照しましょう。計算問題であれば、問題文で与えられるはずです。
- S(H2)0=130.684 J/(mol・K)
- S(O2)0=205.138 J/(mol・K)
- S(H2O)0=69.91 J/(mol・K)
例えば以上のように各物質の標準エントロピーが与えられている場合、標準反応エントロピーΔS0は
$$\begin{align}ΔS^{0}&={S_{H2O}}^{0}-{S_{H2}}^{0}-\frac{1}{2}{S_{O2}}^{0}\\&≒-163.3J/(mol・K)・・・(30)\end{align}$$
(30)式となります。
標準反応エントロピーΔS0が負の値となったので、(26)式の水の生成反応は自発的には起こらないということになります。
この反応を起こしたければ、周囲とのエネルギーのやり取りが必要となってきます。
おわりに
エントロピーを熱力学的な定義や観点から説明しました。
様々な現象がエントロピーの増大する方向に進行していることが定量的にわかります。
ですが、エントロピーは熱力学以外にも統計力学的な意味合いもあり、非常に奥深いパラメータです。
興味のある方は統計力学の意味も勉強してみてください。
