【気体の熱力学】高圧ガス甲種機械：検定試験の出題分野を解説

概要

この記事では高圧ガス甲種機械の出題分野である、気体の熱力学について解説します。

気体の熱力学は毎年春(5月頃)に実施される検定試験、秋(11月頃)の国家試験の両方に出題されており、重要な分野です。

出題内容も気体の熱力学に関してはほとんど被っていますが、問題の形式が検定試験と国家試験で違います。

自分が受ける試験の過去問で問題の形式を把握しつつ勉強していくのが良いと思います。

気体の熱力学の出題分野

気体の熱力学は学識の大問5問中の1問です。

私のような化学工学専門の人にとっては馴染みのある分野であり、絶対に落としてはいけません。

問題構成としては、

・語句の確認問題(小問①)
・計算問題(小問②)

このような形式であることが多いです。

語句の確認問題は選択肢から選ぶタイプか、選択肢がなく自分で用語を記入するタイプどちらも可能性があります。

したがって、用語はきちんと暗記しておく必要があります。

計算問題は等温変化、定圧変化、定容変化、断熱変化の計算であることがほとんどです。

以下の別記事でも解説しています。

それぞれの変化で成立する計算式が異なるため、ちゃんと理論や式を覚えていないと間違えます。

しかしそれほど難しくはありませんから、覚えておけば正解できます。

以下に検定試験で出やすい内容をまとめました。

理想気体の状態方程式

$$PV=nRT・・・(1)$$

P：圧力[Pa]、V：体積[m³]、n：モル量[mol]
R：気体定数[J/(mol・K)]、T：温度[K]

この分野の九九みたいな感じで使用します。知らないとどの問題も解けません。

圧力は問題文中でMPaやkPaで与えられることが多いので単位に注意です。

ボイル・シャルルの法則

$$\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}・・・(2)$$

九九その2です。

ボイル・シャルルの法則そのものを使用するよりは、等温変化でボイルの法則、定圧変化でシャルルの法則みたいに、1つのパラメータを消した状態で使用することが多いです。

計算上は(2)式を覚えておけば問題ないでしょう。

熱力学の第一法則

$$Q=ΔU+W・・・(3)$$

Q：系に外から加えられた熱量[J]、ΔU：系の内部エネルギー変化[J]
W：系が外にした仕事[J]

重要です。

語句の確認問題にしても、計算問題にしても、この熱力学の第一法則をベースにした問題が出題されることが非常に多いです。

常にこの(3)式が使えないかどうか考えながら問題を読むのが良いでしょう。

また、熱量QがkJやMJで与えられることが多いのに対して、内部エネルギーΔUや仕事Wの計算値はJとなることが多いので、単位が合っているかどうか気をつけましょう。

エンタルピー変化

$$ΔH=ΔU+Δ(pV)=ΔU+pΔV+VΔp・・・(4)$$

ΔH：系のエンタルピー変化[J]、p：系の圧力[Pa]
V：系の体積[m³]

出題頻度は低いものの、(4)式のエンタルピー変化が出題されることがあります。

定圧変化、もしくは定容変化で出題された場合には、Δp=0、あるいはΔV=0となりますので計算が簡単になります。

熱力学の第二法則

$$dS=\frac{dQ}{T}・・・(5)$$

dS：微小エントロピー変化[J/K]
Q：系に外から加えられた熱量[J]、T：温度[K]

熱力学の第二法則も甲種機械の検定試験では出題頻度が低いようです。

計算問題でエントロピー計算が出題されることはほとんどなく、語句の確認問題で選択肢に挙がる程度です。

しかし熱力学の第二法則は有名ですし、一般常識的に知っておいた方が良いのは間違いないでしょう。

定容モル熱容量

理想気体の定容モル熱容量C_m,Vは(6)式で定義されています。

$$ΔU=nC_{m,V}ΔT・・・(6)$$

C_m,Vを計算させる問題やC_m,Vの値を与えてΔUを計算させる問題など、出題のされ方は様々であり、出題頻度は高いです。

内部エネルギー変化ΔUを計算させる問題が出たら、すぐに(6)式を使えるよう勉強しておきましょう。

定圧モル熱容量

理想気体の定圧モル熱容量C_m,pは(7)式で定義されています。

$$ΔH=nC_{m,p}ΔT・・・(7)$$

定容モル熱容量と同様に出題されやすいです。
覚えておきましょう。

マイヤーの関係

定圧モル熱容量C_m,pと定容モル熱容量C_m,Vの差が気体定数Rになる関係のことをマイヤーの関係(マイヤーの式)と呼びます。

$$C_{m,p}-C_{m,V}=R・・・(8)$$

R：気体定数[J/(mol・K)]

(8)式で表されます。

定圧モル熱容量C_m,pか定容モル熱容量C_m,Vのどちらか片方が与えられて、マイヤーの関係を使用してもう片方を算出する問題が出題されています。

計算問題だけでなく、語句の確認問題で出題されたこともあるので名前と式をセットで覚えましょう。

等温変化

理想気体を等温変化させる問題は出題頻度が非常に高いです。

変化の前後で温度が一定というだけで、様々な関係式が成り立ちますのでぜひ覚えておきましょう。

ボイル・シャルルの法則から

ボイル・シャルルの法則(2)式から、

$$\frac{p_{1}V_{1}}{T_{1}}=\frac{p_{2}V_{2}}{T_{2}}・・・(2)$$

p：圧力[Pa]、V：気体体積[m³]、T：気体温度[K]

(2)式が成り立ちますが、等温変化であればT₁=T₂ですので、

$$p_{1}V_{1}=p_{2}V_{2}・・・(9)$$

(9)式のボイルの法則が成り立ちます。
(9)式は意外と忘れがちですので注意しましょう。

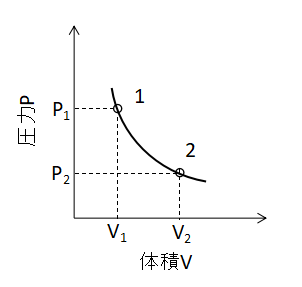
また、縦軸に圧力p、横軸に体積Vを取ったグラフで等温変化を示すと上図のような曲線となります。

このP-Vグラフは問題文で与えられやすいので、それぞれの変化でどのような形のグラフになるかよく覚えておきましょう。

等温変化での仕事

系が外にする仕事Wは、

$$W=\int_{V1}^{V2}pdV=\int_{V1}^{V2}\frac{nRT}{V}dV・・・(10)$$

(10)式で表されます。

ここで、等温変化では温度Tが圧力p、体積Vに依存せず一定とみなせるため、(10)式を積分することができます。

$$\begin{align}W&=nRT[{\rm{ln}}V]^{V_{2}}_{V_{1}}\\&
=nRT{\rm{ln}}(\frac{V_{2}}{V_{1}})=nRT{\rm{ln}}(\frac{p_{1}}{p_{2}})・・・(11)\end{align}$$

積分すると(11)式となります。

(9)式を使用すれば、(11)式のように仕事Wを体積Vの関数、もしくは圧力pの関数で表すことができます。

問題文でどちらのパラメータが与えられるかによって使い分けましょう。

ΔU=0、ΔH=0

定容モル熱容量C_m,Vの関係から、内部エネルギー変化ΔUは(6)式で表されます。

$$ΔU=nC_{m,V}ΔT・・・(6)$$

等温変化ではΔT=0なので、(6)式からΔU=0となります。

同様に定圧モル熱容量C_m,pの関係を表わす(7)式から、等温変化であればΔH=0となります。

定圧変化

ボイル・シャルルの法則から

ボイル・シャルルの法則(2)式について、p₁=p₂とすると、

$$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}・・・(12)$$

(12)式のシャルルの法則が成り立ちます。

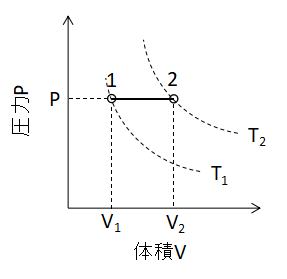
また、P-Vグラフ上で定圧変化を表わすと上図のように直線となります。
わかりやすいですね。

定圧変化での仕事

圧力pが一定とみなせるため、系が外にする仕事Wは、

$$\begin{align}W&=\int_{V1}^{V2}pdV=p[V]^{V_{2}}_{V_{1}}\\&
=p(V_{2}-V_{1})=pΔV・・・(13)\end{align}$$

(13)式のように簡単に積分して求めることができます。

定容変化

ボイル・シャルルの法則から

ボイル・シャルルの法則(7)式について、V₁=V₂とすると、

$$\frac{p_{1}}{T_{1}}=\frac{p_{2}}{T_{2}}・・・(14)$$

(14)式が成り立ちます。

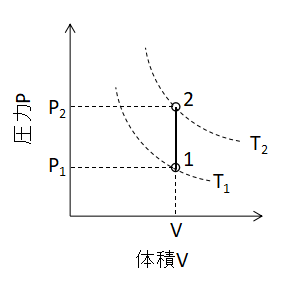
また、同様にP-Vグラフ上で定容変化を表わすと上図のように直線となります。

定容変化での仕事

体積Vが一定とみなせるためΔV＝0となり、系が外にする仕事W=0となります。

定圧変化と混同しないようにしましょう。

断熱変化

断熱変化をP-Vグラフで表すと上図のようになります。

1→2への変化前後でP、V、T全てが変化するため、P-Vグラフにおいてはあまり特徴的ではありません。

ただし、カルノーサイクルで断熱変化はよく出てくるので覚えておいて損はないです。

熱力学の第一法則から

断熱変化の場合は、熱力学の第一法則(3)式とマイヤーの関係(8)式から、次の(15)式が導出できます。

$$p_{1}V_{1}^{γ}=p_{2}V_{2}^{γ}・・・(15)$$

γ：比熱容量の比[-]

(15)式は式の形も簡単なので覚えておきましょう。

断熱変化での仕事

断熱変化における仕事Wは(15)式を使用して導出します。

(15)式から

$$pV^{γ}=p_{1}V_{1}^{γ}$$

$$p=p_{1}(\frac{V_{1}}{V})^{γ}$$

と変形して仕事の定義式に代入します。

$$\begin{align}W&=\int_{V1}^{V2}p_{1}(\frac{V_{1}}{V})^{γ}dV
=p_{1}V_{1}^{γ}[-\frac{1}{γ-1}V^{-(γ-1)}]^{V_{2}}_{V_{1}}\\&
=\frac{p_{1}V_{1}^{γ}}{γ-1}(V_{1}^{-(γ-1)}-V_{2}^{-(γ-1)})=\frac{p_{1}V_{1}}{γ-1}\Biggl(\frac{V_{1}^{-(γ-1)}}{V_{1}^{-(γ-1)}}-\frac{V_{2}^{-(γ-1)}}{V_{1}^{-(γ-1)}}\Biggr)\\&
=\frac{p_{1}V_{1}}{γ-1}\Bigl(1-(\frac{V_{1}}{V_{2}})^{γ-1}\Bigr)=\frac{p_{1}V_{1}}{γ-1}\Bigl(1-(\frac{p_{2}}{p_{1}})^{\frac{γ-1}{γ}}\Bigr)・・・(16)\end{align}$$

最終的に(16)式の形となります。

覚えられるなら覚えた方が良いですが、難しそうなら試験中に導出するのもアリだと思います。

また断熱変化の場合、定容モル熱容量C_m,Vと比熱容量の比γの関係から仕事Wを求めることができます。

(3)式と断熱変化でQ=0であるので、

$$W=-ΔU$$

(6)式の定容モル熱容量C_m,Vから、

$$W=-ΔU=nC_{m,V}(T_{1}-T_{2})・・・(17)$$

となります。
ここで比熱容量の比γは、γ=C_m,p/C_m,Vで定義されています。

この定義と(8)式のマイヤーの関係から、

$$γC_{m,V}-C_{m,V}=R$$

$$C_{m,V}=\frac{R}{γ-1}・・・(18)$$

(18)式を(17)式に代入し、

$$W=\frac{nR}{γ-1}(T_{1}-T_{2})・・・(19)$$

(19)式が導出されます。

この式も導出が簡単なので、無理に覚えるより必要なら試験中に導出するくらいで良いと思います。

カルノーサイクル

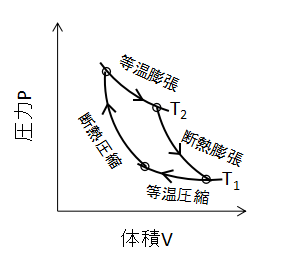
上図にカルノーサイクルの変化を示します。

2つの等温変化と2つの断熱変化を組み合わせたサイクルで、理論上最も効率が良いとされています。

サイクルが行なう仕事Wは、

$$W=Q_{2}-Q_{1}・・・(20)$$

Q₂：等温膨張時に加えた熱量[J]、Q₁：等温圧縮時に放出した熱量[J]

(20)式で表されます。

また、仕事の効率ηは、

$$η=\frac{W}{Q_{2}}=1-\frac{Q_{1}}{Q_{2}}=1-\frac{T_{1}}{T_{2}}・・・(21)$$

(21)式で表されます。

ただ、カルノーサイクルの効率よりは等温変化、断熱変化の仕事Wを計算させる問題が多い気がします。

それぞれの変化での仕事の算出方法をきちんと理解しておきましょう。

まとめ

高圧ガス甲種機械の検定試験範囲である、気体の熱力学についてまとめました。
この記事に書いてあるくらいの内容をマスターしておけば大丈夫だと思います。

単に式を覚えるだけでは不十分で、過去問などの練習問題をこなして問題文でどのように式が使用されているか確認しましょう。