概要
この記事ではエネルギー管理士(熱分野)の出題分野である、熱利用設備(冷凍・空気調和設備)について解説します。
熱利用設備(冷凍・空気調和設備)は課目Ⅳ"熱利用設備及びその管理"の中で、選択問題として出題されています。
冷凍サイクルの内容は多少課目Ⅱと被っていますが、空調関係の内容は新たに勉強する必要があります。
以下で出題頻度が高かった内容を紹介しています。
空調用語
空調に関する用語がそのまま出題されることもありますし、他の問題も用語を知っていないと解けません。
まずは基本から勉強しましょう。
湿り空気
一般的に大気の組成は乾燥空気で表されます。主要な組成として、
- 窒素:78.08vol%
- 酸素:20.95vol%
- アルゴン:0.93vol%
- 二酸化炭素:0.04vol%
などが含まれます。
実際の大気は、乾燥空気にプラスして水蒸気が若干含まれます。これを湿り空気といいます。
空調の分野では常に湿り空気を扱うことになり、特記がない限り空気といえば湿り空気を指します。
湿度
絶対湿度x
乾燥空気1kg当たりに含まれている水蒸気の量[kg]で表されるものが絶対湿度x[kg/kg(DA)]です。DAはDry Airの略です。
相対湿度φ
ある空気の飽和水蒸気圧に対する水蒸気分圧を相対湿度といいます。日常生活で湿度〇〇%とよく聞く値は相対湿度です。
相対湿度φは以下の式で計算できます。
$$φ=(\frac{P_{w}}{P_{ws}})×100・・・(1)$$
Pw:空気の水蒸気分圧、Pws:空気の飽和水蒸気圧
空気線図
空調を考える上では、湿り空気の物性が非常に重要となります。
そこで湿り空気の物性を知るために、温度、湿度、比エンタルピー、比容積等のうち、2つを直交座標軸で表し、残りを斜交座標で表したものを湿り空気線図、もしくは単に空気線図といいます。
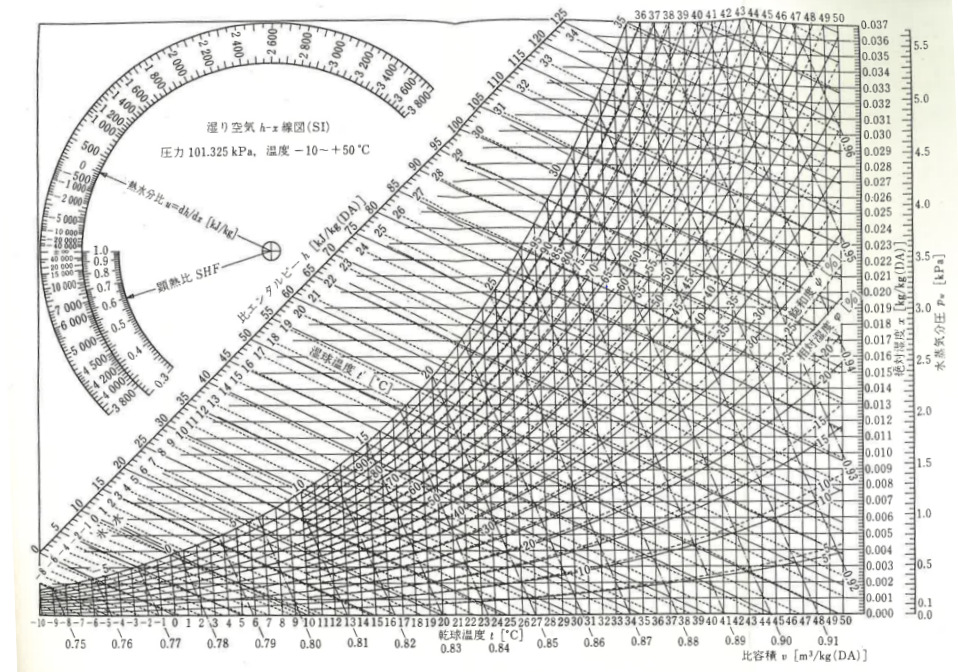
"エネルギー管理士試験講座 熱分野Ⅳ"より引用
上図に空気線図を示します。
縦軸に絶対湿度x、横軸に乾球温度tを取っています。一方で比エンタルピーh、比容積v、相対湿度φなどは斜交座標で取っています。
また、左上には熱水分比uと顕熱比SHFの補助線図があり、作図で使用します。
湿り空気の比エンタルピー
湿り空気の比エンタルピーhは、乾き空気の比エンタルピーhaに水の蒸発潜熱分を足した値となるので、
$$\begin{align}h&=h_{a}+h_{w}x\\&=C_{p}t+(C_{p}'t+r)x・・・(2)\end{align}$$
h:湿り空気の比エンタルピー[kJ/kg(DA)]、ha:乾き空気の比エンタルピー[kJ/kg(DA)]
hw:水蒸気の比エンタルピー[kJ/kg(DA)]、x:湿り空気の絶対湿度[kg/kg(DA)]
Cp:乾き空気の比熱[kJ/(kg・K)]、Cp':水蒸気の比熱[kJ/(kg・K)]
r:水の蒸発潜熱[kJ/kg]、t:乾球温度[℃]
(2)式で表されます。
したがって、Cp、Cp'、rが与えられれば、縦軸の絶対湿度x、横軸の乾球温度tから計算することができます。
空気線図があれば、計算せずともx,tの値から比エンタルピーhを斜交座標から直接読み取れます。
加熱・冷却
絶対湿度一定で湿り空気の加熱・冷却を行なう場合、空気線図上では横方向に状態が変化します。

このときの空気のエンタルピー変化量Δhは、
$$Δh=h_{1}-h_{2}=(C_{p}+C_{p}'x)(t_{1}-t_{2})・・・(3)$$
h1:状態1での比エンタルピー[kJ/kg]、h2:状態2での比エンタルピー[kJ/kg]
(3)式で計算できます。
また、加熱・冷却に必要な交換熱量Qは、
$$Q=(h_{1}-h_{2})G=(h_{1}-h_{2})\frac{V}{v}・・・(4)$$
G:乾き空気の質量流量[kg/h]、V:標準風量[m3/h]
v=0.83:標準空気の比容積[m3/kg(DA)]
(4)式で計算できます。
冷却・減湿
空気を下図のように状態1から状態2まで冷却・減湿する場合を考えます。

エンタルピーの変化量は、
$$Δh=h_{1}-h_{2}・・・(5)$$
(5)式で表されます。
また、冷却・減湿に必要な交換熱量Qは同様に(4)式で計算できます。
加湿
空気を加湿する場合、状態変化の方向は空気線図上の左上にある熱水分比uと同じ方向となります。
$$u=\frac{dh}{dx}・・・(6)$$
熱水分比uは(6)式で定義されています。
実用上は、加湿のために空気中に噴霧する水分の比エンタルピーhL[kJ/kg]を使用して、
$$u=h_{L}・・・(7)$$
熱水分比は(7)式となります。
(7)式で求めたuから、熱水分比の補助線図で傾きを確認します。
次に状態1から状態2へと変化するときの傾きが補助線図の傾きと一致するように直線を引けば、加湿の変化を表わすことができます。
ただ、エネルギー管理士は定規などの作図を補助する用具の持ち込みは禁止なので、作図自体をすることはないでしょう。
しかし熱水分比は出題される可能性があるので意味合いは覚えておきましょう。以下に加湿の具体例を示します。
水噴霧による加湿
20℃の水を空気に噴霧すると考えます。
そのエンタルピーは83.9kJ/kgなので、熱水分比u=83.9kJ/kgとなります。
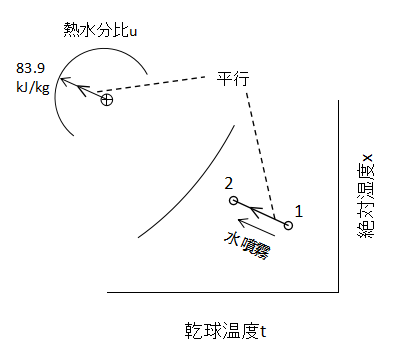
上図に示すようにu=83.9kJ/kgの傾きは、補助線図上では左上方向の傾きとなっています。
したがって、状態1から加湿して状態2へと変化するときの傾きも同じ方向となります。
蒸気噴霧による加湿
大気圧の蒸気を空気に噴霧すると考えます。
そのエンタルピーは2,676kJ/kgなので、熱水分比u=2,676kJ/kgとなります。
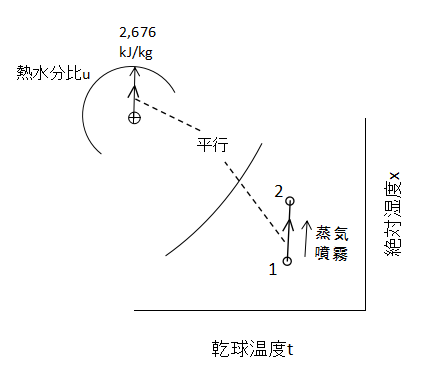
上図に示すようにu=2,676kJ/kgの傾きは、補助線図上ではほぼ真上方向の傾きとなっています。
したがって、状態1から加湿して状態2へと変化するときの傾きも同じ方向となります。
試験では加湿する場合の状態変化の方向や、水噴霧・蒸気噴霧の傾きを問う問題が出題されたことがあるので、ぜひ覚えておきましょう。
空気の混合
二つの状態の異なる空気G1[kg(DA)]、G2[kg(DA)]を混合する場合を考えます。
混合後の空気の状態は、下図に示すように点1と点2を結んだ直線上の点3となります。
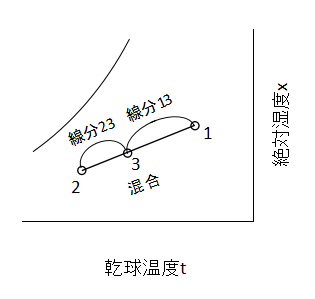
加えてG1、G2と線分13、線分23の長さに関して、
$$\frac{G_{2}}{G_{1}}=\frac{線分13}{線分23}・・・(8)$$
(8)式が成り立ちます。
また、点3の空調機の送風量G3[kg(DA)]がわかっている場合は、
$$\frac{G_{1}}{G_{3}}=\frac{線分23}{線分13+線分23}・・・(9)$$
$$\frac{G_{2}}{G_{3}}=\frac{線分13}{線分13+線分23}・・・(10)$$
以上の式でG1やG2を算出することもできます。
顕熱比SHF
空調の熱負荷計算は、顕熱負荷と潜熱負荷に分けることができます。
全熱負荷に対する顕熱負荷を割合をSHFといいます。
$$SHF=\frac{顕熱負荷}{顕熱負荷+潜熱負荷}・・・(11)$$
SHFは(11)式で計算できます。
SHFも熱水分比uと同様に、空気線図上の補助線図があります。

(11)式からSHFの値を求め、補助線図から状態変化するときの傾きを読み取ります。
状態1が室内の空気の状態で、補助線図の傾きを状態1から引いた線上に給気の状態を取ることになります。
空調プロセス
冷房と暖房のどちらかはほぼ毎年出題されており、重要です。
冷房時の空調プロセス
冷房時の空調プロセスを空気線図上で表したグラフを以下に示します。
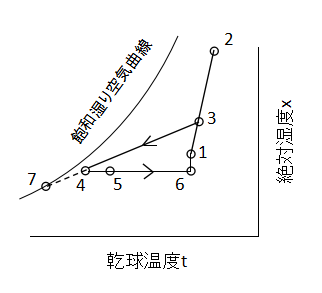
①:計画室内状態
②:外気状態
③:①と②の混合後の状態
③→④:表面温度⑦のコイルによる冷却
④:冷却後の状態
④→⑤:送風時のダクト等からの入熱による温度上昇
⑤:温度上昇後の状態
⑤→⑥:室内での顕熱負荷による温度上昇
⑥:温度上昇後の状態
⑥→①:室内の湿分吸収(潜熱負荷)による絶対湿度増加
⑦:冷却コイルの平均表面温度
各点がどのような状態や操作となっているかが出題されることが多いので、よく覚えておきましょう。
暖房時の空調プロセス
暖房時の空調プロセスを空気線図上で表したグラフを以下に示します。
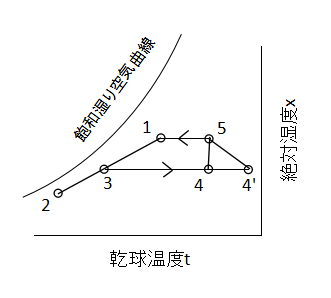
①:計画室内状態
②:外気状態
③:①と②の混合後の状態
③→④:③の混合空気をコイルで加熱
④、④':加熱後の状態
④→⑤:室内への蒸気噴霧による加湿
④'→⑤:室内への水噴霧による加湿
⑤:加湿後の状態
⑤→①:室内での顕熱負荷による温度低下
暖房プロセスでは加湿方法の違いが出題されることが多いです。
加湿による④→⑤または④'→⑤の移動の傾きは前述した熱水分比uからわかります。
蒸気加湿の場合は、⑤の温度がわずかに上昇するため右肩上がりの傾きとなりますが、実質はほぼ真上に移動します。
水噴霧加湿の場合は、噴霧された水が蒸発することで潜熱により温度低下しますので、右肩下がりの傾きとなります。
空調設備の省エネルギー
2,3年に1度くらいは空調設備の省エネルギーに関する内容が出題されています。
常識的にわかるような問題もありますが、知らなければわからない問題もあります。
以下に過去出題されたことのある省エネルギー対策を示します。
- 室内条件の設定変更:1年中同じ条件で設定するよりも、季節等に応じて条件を変更した方が省エネとなる。
- ポンプのインバータ制御・台数制御:空調負荷変動が大きい場合に、冷温水ポンプの動力を抑えるために有効。
- 外気冷房:外気の温度や湿度が室内よりも低い場合は、外気を多く取り入れて空調機動力を削減する。
- 外気カット制御:予冷予熱時に在室者がいない場合に、空調機への外気導入を中止して空調機負荷を削減する。
- 排熱回収(全熱交換器):室内空気と外気からの給気で熱回収する。
- 炭酸ガス(CO2)濃度制御:室内のCO2濃度に応じて換気量を制御する。
- ナイトパージ:夜間の外気が室内温度より低い場合に、室内に取り入れて空調機負荷を削減する。
ヒートポンプ・冷凍機
通常、熱は高温部から低温部へ流れるもので、低温部から高温部に自然に流れることはありません。
例えば、水を低い位置から高い位置へと輸送するのにポンプが必要なように、熱も低温部から高温部へと移動させるためには外部からエネルギーを加える必要があります。
低温部から高温部へと熱を移動させるシステムをヒートポンプといいます。
ヒートポンプは低温部から高温部へと移動させる目的によって名称が変わります。
- ヒートポンプ:暖房や湯沸かしなど加熱の目的で使用
- 冷凍機:冷房、冷蔵庫など冷却の目的で使用
ヒートポンプと冷凍機は原理的に全く同じもので、以上のように目的が異なります。
冷凍(ヒートポンプ)サイクル
冷凍機のサイクルとヒートポンプのサイクルは基本的に同一ですが、試験では冷凍サイクルとして出題されることが多いようです。
ここでは冷凍サイクルとして説明します。
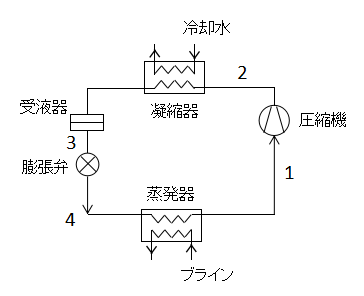
上図に圧縮機を使用した冷凍サイクルの構成要素を示します。

加えて、縦軸に圧力P、横軸に比エンタルピーhを取ったp-h線図を示します。この線図はモリエ線図と呼ばれることもあります。
1→2(圧縮機での断熱圧縮)
蒸発器で発生した蒸気を断熱圧縮し高温高圧の過熱蒸気にします。
p-h線図上ではわかりにくいですが、この操作は等エントロピー変化となります。
2→3(凝縮器での等圧放熱)
凝縮器で過熱蒸気が冷却水に熱を与え、蒸気は液化します。
p-h線図上では、状態3が飽和液線よりも左にきていることから、蒸気が液化していることがわかります。
等圧条件下で凝縮させるため、比エンタルピーのみが減少し、線図上を左に移動します。
3→4(膨張弁での絞り膨張)
膨張弁で減圧され、液体が膨張し湿り蒸気となります。
p-h線図上では、状態4が飽和液線よりも右にきていることから、湿り蒸気となっていることがわかります。
比エンタルピーは一定で、圧力のみが減少するため、線図上を下方向に移動します。
4→1(蒸発器での蒸発)
蒸発器で冷却媒体から熱を奪って冷却し、サイクル流体は奪った熱によって蒸発します。
p-h線図上では、状態1が飽和蒸気線よりも右側にきているため、飽和蒸気ではなく過熱蒸気となっています。
等圧条件下で熱のやり取りをするため、比エンタルピーのみが増加し、線図上を右に移動します。
過去の試験ではそれぞれのサイクルの操作や状態が出題されたことがあります。
成績係数
冷凍機やヒートポンプの能力は成績係数(Coefficient of Performance)もしくはCOPと呼ばれる指標で表します。
冷凍機の成績係数εrは、圧縮機で加えたエネルギー(1→2)に対して、どれだけの冷却効果があるか(4→1)で表されます。したがって、
$$ε_{r}=\frac{h_{1}-h_{4}}{h_{2}-h_{1}}・・・(12)$$
h1:状態1の比エンタルピー[kJ/kg]、h2:状態2の比エンタルピー[kJ/kg]
h4:状態4の比エンタルピー[kJ/kg]
成績係数εrは(12)式となります。
また、ヒートポンプの成績係数εhは、圧縮機で加えたエネルギー(1→2)に対して、どれだけの加熱効果があるか(2→3)で表されます。したがって、
$$\begin{align}ε_{h}&=\frac{h_{2}-h_{3}}{h_{2}-h_{1}}=\frac{(h_{2}-h_{1})+(h_{1}-h_{4})}{h_{2}-h_{1}}\\&=1+ε_{r}・・・(13)\end{align}$$
(13)式となります。
おわりに
エネルギー管理士(熱分野)課目Ⅳの熱利用設備(冷凍・空気調和設備)の分野について解説しました。
特に空気線図に関する内容は頻出ですので、ここだけはできるようになっておきましょう。
