概要
活量係数を算出する手法の1つであるWilson式は2液相分離する系に適用できないことが一般的に知られています。
ですが、なぜ適用できないのかきちんと確認したことがある人は少ないのではないでしょうか。
本記事ではWilson式の2液相への適用可否について紹介します。
相分離する場合のギブス自由エネルギー変化
2成分が混合する場合は混合物のギブス自由エネルギーΔGmixが小さくなり、下に凸のグラフとなります。
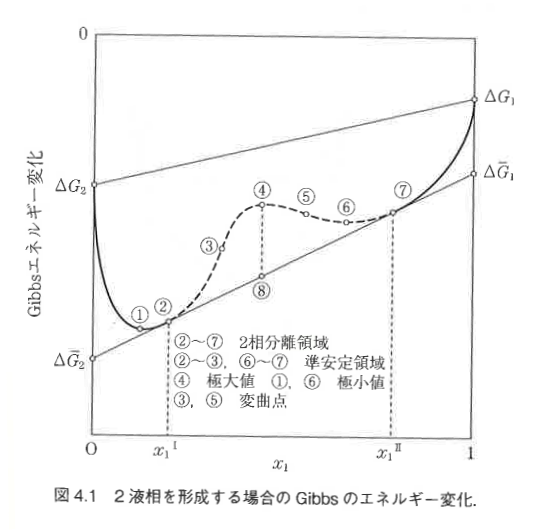
一方で相分離する系では上のグラフのような上に凸の極大値を示します。
点線で記載されている②~⑦の組成領域はギブス自由エネルギーが高くなっているため、混合するよりも相分離した方が安定な領域となっています。
したがってギブス自由エネルギー変化ΔGの関数が極値を持ち、かつ上に凸であることが2液相分離する条件となります。
数学的に極値を持つ条件は、
$$\frac{∂ΔG}{∂x_{1}}=0・・・(1)$$
(1)式となります。
上に凸の関数となる条件は、
$$\frac{∂^{2}ΔG}{∂x_{1}^{2}}<0・・・(2)$$
(2)式となります。
(1)、(2)式の両方が成り立てば2液相分離すると言えます。
Wilson式は(2)式が成り立たないため、2液相分離を表わすことができません。
Wilson式が2液相に適用できないことの証明
Wilson式が2液相に適用できないことを証明するには、(2)式が成り立たないことを証明できれば良いです。
(2)式が成り立たないためには、
$$\frac{∂^{2}ΔG}{∂x_{1}^{2}}≧0・・・(3)$$
(3)式を証明すれば良いですよね。
Wilson式における混合物のギブス自由エネルギー変化ΔGはこちらの記事の(6)、(7)、(8)式を引用し、
$$\begin{align}\frac{g^{E}}{RT}&
=-x_{1}{\rm{ln}}(x_{1}+Λ_{12}x_{2})-x_{2}{\rm{ln}}(x_{2}+Λ_{21}x_{1})・・・(6)'\end{align}$$
$$g^{m}=g^{i}+g^{E}・・・(7)'$$
$$g^{i}=RT(x_{1}{\rm{ln}}x_{1}+x_{2}{\rm{ln}}x_{2})・・・(8)'$$
となり、整理すると
$$\begin{align}\frac{g^{m}}{RT}=\frac{ΔG}{RT}=&-x_{1}{\rm{ln}}(x_{1}+Λ_{12}x_{2})-x_{2}{\rm{ln}}(x_{2}+Λ_{21}x_{1})\\&+(x_{1}{\rm{ln}}x_{1}+x_{2}{\rm{ln}}x_{2})・・・(4)\end{align}$$
(4)式となります。
この(4)式をx1について二階微分して式変形していきます。
まず一階微分です。
$$\begin{align}\frac{∂}{∂x_{1}}\frac{ΔG}{RT}=&
-{\rm{ln}}(x_{1}+Λ_{12}x_{2})-x_{1}\frac{1-Λ_{12}}{x_{1}+Λ_{12}x_{2}}\\&
+{\rm{ln}}(x_{2}+Λ_{21}x_{1})-x_{2}\frac{Λ_{21}-1}{x_{2}+Λ_{21}x_{1}}+{\rm{ln}}x_{1}-{\rm{ln}}x_{2}\end{align}$$
続いて二階微分です。
$$\begin{align}\frac{∂^{2}}{∂x_{1}^{2}}\frac{ΔG}{RT}&=
-\frac{1-Λ_{12}}{x_{1}+Λ_{12}x_{2}}-\frac{1-Λ_{12}}{x_{1}+Λ_{12}x_{2}}+x_{1}(\frac{1-Λ_{12}}{x_{1}+Λ_{12}x_{2}})^{2}\\&
+\frac{Λ_{21}-1}{x_{2}+Λ_{21}x_{1}}+\frac{Λ_{21}-1}{x_{2}+Λ_{21}x_{1}}+x_{2}(\frac{Λ_{21}-1}{x_{2}+Λ_{21}x_{1}})^{2}+\frac{1}{x_{1}}+\frac{1}{x_{2}}\\&
=\frac{-2x_{1}(1-Λ_{12})(x_{1}+Λ_{12}x_{2})+x_{1}^{2}(1-Λ_{12})^{2}+(x_{1}+Λ_{12}x_{2})^{2}}{x_{1}(x_{1}+Λ_{12}x_{2})^{2}}\\&
+\frac{2x_{2}(Λ_{21}-1)(x_{2}+Λ_{21}x_{1})+x_{2}^{2}(Λ_{21}-1)^{2}+(x_{2}+Λ_{21}x_{1})^2}{x_{2}(x_{2}+Λ_{21}x_{1})^{2}}\\&
=\frac{Λ_{12}^{2}(x_{1}+x_{2})^{2}}{x_{1}(x_{1}+Λ_{12}x_{2})^{2}}+\frac{Λ_{21}^{2}(x_{1}+x_{2})^{2}}{x_{2}(x_{2}+Λ_{21}x_{1})^{2}}\\&
=\frac{Λ_{12}^{2}}{x_{1}(x_{1}+Λ_{12}x_{2})^{2}}+\frac{Λ_{21}^{2}}{x_{2}(x_{2}+Λ_{21}x_{1})^{2}}・・・(5)\end{align}$$
変形していくと最終的に(5)式の形となります。
x1、x2は成分1,2のモル分率なので必ず正の値を取ります。
よって(5)式から
$$\frac{∂^{2}}{∂x_{1}^{2}}\frac{ΔG}{RT}≧0$$
であることが証明できました。
このことからWilson式は2液相分離する系に適用しても、ギブス自由エネルギー変化ΔGが上に凸となる関数を表現できないため、適用すべきではないと言えます。
