概要
ある2成分がどれだけ蒸留分離しやすいのかを示す指標を相対揮発度、もしくは比揮発度といいます。
$$相対揮発度α_{AB}=\frac{K_{A}}{K_{B}}=\frac{y_{A}/x_{A}}{y_{B}/x_{B}}・・・(1)$$
KA:成分Aの平衡係数(平衡比)、KB:成分Bの平衡係数(平衡比)
yA,yB:成分A,Bの気相モル分率、xA,xB:成分A,Bの液相モル分率
相対揮発度αABは一般に(1)式で表されます。
(1)式に(2)、(3)式を代入してyAについて整理すると、
$$x_{A}+x_{B}=1・・・(2)$$
$$y_{A}+y_{B}=1・・・(3)$$
$$y_{A}=\frac{α_{AB}x_{A}}{(α_{AB}-1)x_{A}+1}・・・(4)$$
(4)式となります。
(4)式がxy線図で言うところの気液平衡曲線の式となります。
つまり、相対揮発度αABがわかれば気液平衡曲線が書けるということです。
ただし相対揮発度は(1)式から、2成分の組成によって変化するため、厳密には蒸留塔の各段ごとに相対揮発度を計算する必要があります。
理想系での相対揮発度
Raoultの法則が成り立つ理想溶液と考えると、(1)式は
$$相対揮発度α_{AB}=\frac{P_{A}}{P_{B}}・・・(5)$$
PA:成分Aの蒸気圧、PB:成分Bの蒸気圧
(5)式で表すことができます。
(5)式は相対揮発度αが、成分Bに対して成分Aがどれだけ蒸発しやすいのか(蒸気圧が高いのか)、ということをわかりやすく意味しています。
各成分の蒸気圧は一般的にAntoine式から算出することが多いです。
詳しくは蒸気圧の推算方法に関する記事を見てください。
-

【純物質の蒸気圧】推算方法を解説:Antoine式が精度高い
蒸気圧とは気体と液体が平衡関係にある場合の気相の圧力のことで、化学プラントの装置設計においては非常に重要な物性です。特に蒸留塔のような2成分以上の混合物の気液平衡を扱う場合に、まず純物質の蒸気圧を算出する必要があります。
続きを見る
Antoine式では、蒸気圧Pは温度Tの関数となっています。
したがって、定温条件下では(5)式から相対揮発度αは一定値を示します。
一方で、定圧条件下では温度変化によって各成分の蒸気圧は変化しますから、相対揮発度も変化します。
この場合には一般的に相対揮発度の幾何平均値αAVを使用します。
$$α_{av}=\sqrt{α_{A}α_{B}}・・・(6)$$
αA:成分Aの沸点における相対揮発度、αB:成分Bの沸点における相対揮発度
(6)式に示すように、各成分の沸点における相対揮発度を使用して幾何平均値を求めます。
相対揮発度の値とxy線図
(5)式において、通常は分子に蒸発しやすく蒸気圧が高い成分を持ってくるので、相対揮発度αは1以上の数字となります。
α≒1の場合
相対揮発度αが1に近いと2成分の蒸気圧がほぼ同じということなので、蒸留分離しにくいということになります。
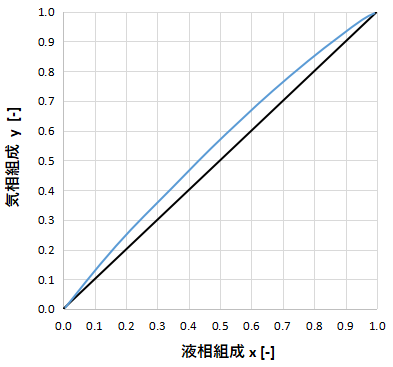
上のグラフに相対揮発度が1に近い場合のxy線図を示します。
気液平衡曲線がy=xに近いため、蒸留分離しようと思うと蒸留塔の段数が多く必要となることがわかります。
現実的にはα>1.2程度であれば蒸留でなんとか分離できると言われています。
1≦α≦1.2であれば、蒸留ではあまりにも段数が多くなってしまうので非現実的です。
他の成分を投入して相対揮発度を変化させるか、別の分離方法に変えるか工夫が必要です。
α>>1の場合
相対揮発度αが1よりも圧倒的に大きいと2成分の蒸気圧にかなり差があるということなので、蒸留分離しやすいということになります。

上のグラフに相対揮発度が1より圧倒的に大きい場合のxy線図を示します。
気液平衡曲線がy=xから離れているため、蒸留塔1段あたりの分離効率が良く、蒸留が容易であることがわかります。
おわりに
蒸留分離のしやすさの指標である相対揮発度について解説しました。
蒸留塔の設計をする前に相対揮発度がどのくらいの値となるか確認しておくのがよいでしょう。
