【混合量】を解説：混合物の組成平均値と混合特性値の差異

概要

工業的に扱う流体はほとんど全て混合物であるため、混合物の物性をなるべく正確に予測することは重要です。

その一方で混合物の物性は、各成分の純物性値の組成平均を取った値からずれが生じることが一般的に知られています。

温度・圧力一定条件下における、純物性値m_iの組成平均値と実際の混合特性値mとの差異を混合量Δmといいます。

実用上は、混合量Δmを以下に精度良く求めるかが課題となっています。

混合量

定義

わかりやすいように2成分系の混合量について考えます。

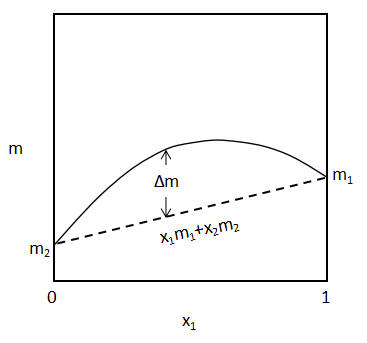
上図に2成分系混合量の図式表現を示しました。

何らかの状態量mの混合量をΔmとしています。(mはエンタルピー、エントロピー、ギブス自由エネルギー、体積などが挙げられます。)

図の点線部分が成分1,2の組成平均値x₁m₁+x₂m₂を示しています。

混合量Δmは、

$$Δm=m-\sum_{i}(x_{i}m_{i})・・・(1)$$

(1)式のように、混合特性m_iと組成平均値との差で表されます。

図では混合量Δmはプラスの値に見えますが、マイナスの値となる場合もあります。

混合体積の計算例

例として、500cm³のエタノール(成分1)と500cm³の水(成分2)を25℃一定下で混合させたときの体積を求めてみましょう。

条件として、

• V₁=58.55cm³/mol
• V₂=18.06cm³/mol
• 混合体積ΔV=-0.73cm³/mol

以上の条件が与えられているとします。

まず、各成分のモル数と全体のモル数を求めます。

$$V_{1}=500/58.55≒8.54 \rm{mol}・・・(2)$$

$$V_{2}=500/18.06≒27.69 \rm{mol}・・・(3)$$

$$V_{total}=8.54+27.69=36.23 \rm{mol}・・・(4)$$

(1)式から、混合溶液の体積Vは、

$$\begin{align}V&=ΔV+\sum_{i=2}(x_{i}V_{i})\\&=-0.73×36.23+8.54×58.55+27.69×18.06\\&≒973.65 \rm{cm^{3}}・・・(5)\end{align}$$

(5)式のように求められます。

部分モル量

混合量Δmに関連する概念として部分モル量m_i___が挙げられます。

部分モル量の定義は(6)式で表されます。

$$\overline{m_{i}}=\Bigl(\frac{∂(n_{T}m)}{∂n_{i}}\Bigr)_{T,P,n_{j}}・・・(6)$$

この部分モル量を利用して、混合量Δmは

$$Δm=\sum x_{i}(\overline{m_{i}}-m_{i})・・・(7)$$

(7)式で表されます。

したがって、部分モル量m_i___は混合物の状態量を組成平均値で表すための仮想的な量としての意味合いを持ちます。

部分モル量の詳細は以下の記事で解説しています。

過剰量

過剰量は実在混合物と理想混合物の状態量の差を過剰量といい、(7)式で定義されます。

$$m^{E}=m-m^{id}・・・(1)$$

m^E：過剰量、m：実在混合物の状態量、m^id：理想混合物の状態量

実在混合物の混合量を求める際に、非常に便利な概念です。

過剰量の詳細は以下の記事で解説しています。

おわりに

混合量について解説しました。

化学工学ではほとんどの場合に混合物を扱うため、混合物性や状態量をどのように求めるかが非常に重要です。

混合量は混合物の理論の基礎的な概念ですので、ぜひ覚えておきましょう。