概要
混合物1mol当たりの状態量に対して、任意のi成分だけをdniだけ微小変化させたときの状態量の変化量を部分モル量miといいます。
混合物の組成を変化させたとき、混合物の物性値が純物質物性値の組成平均から計算される値からずれることがよくあります。
このときの組成平均から計算される値との差異を混合量といい、部分モル量は混合量をを計算する手法の1つです。
加えて部分モル量は活量係数モデル等の気液平衡モデルを考えるうえで基礎的な概念となっています。
部分モル量の定義
定義
まず部分モル量の定義について解説します。
ある示量性状態量mと系全体のモル数nTの積であるnTmを全微分します。(ただし、j≠i)
$$d(n_{T}m)=\Bigl(\frac{∂(n_{T}m)}{∂T}\Bigr)_{P,n_{i}}dT+\Bigl(\frac{∂(n_{T}m)}{∂P}\Bigr)_{T,n_{i}}dP+\sum\Bigl(\frac{∂(n_{T}m)}{∂n_{i}}\Bigr)_{T,P,n_{j}}dn_{i}・・・(1)$$
(1)式において、温度T・圧力Pを一定にして、混合物の組成niを変化させると、
$$d(n_{T}m)=\sum\Bigl(\frac{∂(n_{T}m)}{∂n_{i}}\Bigr)_{T,P,n_{j}}dn_{i}・・・(2)$$
(2)式となります。
(2)式における個々の微分を部分モル量miといい、(3)式で表されます。
$$\overline{m_{i}}=\Bigl(\frac{∂(n_{T}m)}{∂n_{i}}\Bigr)_{T,P,n_{j}}・・・(3)$$
混合量と部分モル量
(2)、(3)式からnTmは
$$n_{T}m=\sum n_{i}\overline{m_{i}}・・・(4)$$
(4)式のように各成分のモル量と部分モル量の積の和で表されます。
(4)式を両辺nTで割ると、
$$m=\sum x_{i}\overline{m_{i}}・・・(5)$$
示量性状態量mは部分モル量の組成の平均値で表すことができます。
また、混合量Δmの定義は
$$Δm=m-\sum x_{i}m_{i}・・・(6)$$
(6)式となっており、(5)式を代入すると、
$$Δm=\sum x_{i}(\overline{m_{i}}-m_{i})・・・(7)$$
(7)式のように混合量Δmと部分モル量miの関係式が得られます。
図による表現
部分モル量と混合量を図示するとどうなるのか考察してみましょう。
(3)式を全微分すると、
$$\overline{m_{i}}=m\Bigl(\frac{∂n_{T}}{∂n_{i}}\Bigr)_{T,P,n_{j}}+n_{T}\Bigl(\frac{∂m}{∂n_{i}}\Bigr)_{T,P,n_{j}}・・・(8)$$
(8)式となります。
次に、
$$\Bigl(\frac{∂(n_{T})}{∂n_{i}}\Bigr)_{T,P,n_{j}}=\Bigl(\frac{∂(n_{1}+n_{2})}{∂n_{i}}\Bigr)_{T,P,n_{j}}=1・・・(9)$$
(9)式が成り立つため、(8)式に代入することで、
$$\overline{m_{i}}=m+n_{T}\Bigl(\frac{∂m}{∂n_{i}}\Bigr)_{T,P,n_{j}}・・・(10)$$
(10)式が得られます。
次に2成分系において(10)式を考えると、成分1,2それぞれで(11)、(12)式が成り立ちます。
$$\overline{m_{1}}=m+n_{T}\Bigl(\frac{∂m}{∂n_{1}}\Bigr)_{T,P}・・・(11)$$
$$\overline{m_{2}}=m+n_{T}\Bigl(\frac{∂m}{∂n_{2}}\Bigr)_{T,P}・・・(12)$$
ここで、∂m/∂n1について、
$$\frac{∂m}{∂n_{1}}=\frac{∂m}{∂x_{2}} \frac{∂x_{2}}{∂n_{1}}=\frac{∂m}{∂x_{2}} \frac{∂}{∂n_{1}}\Bigl(\frac{n_{2}}{n_{1}+n_{2}}\Bigr)=-\frac{∂m}{∂x_{2}} \frac{n_{2}}{(n_{1}+n_{2})^{2}}=-\frac{∂m}{∂x_{2}} \frac{x_{2}}{n_{T}}・・・(13)$$
(13)式となります。同様に∂m/∂n2についても
$$\frac{∂m}{∂n_{2}}=\frac{∂m}{∂x_{1}} \frac{∂x_{1}}{∂n_{2}}=\frac{∂m}{∂x_{1}} \frac{∂}{∂n_{2}}\Bigl(\frac{n_{1}}{n_{1}+n_{2}}\Bigr)=-\frac{∂m}{∂x_{1}} \frac{n_{1}}{(n_{1}+n_{2})^{2}}=-\frac{∂m}{∂x_{1}} \frac{x_{1}}{n_{T}}・・・(14)$$
(14)式となります。
(13)、(14)式を(11)、(12)式に代入すると、
$$\overline{m_{1}}=m-x_{2}\Bigl(\frac{∂m}{∂x_{2}}\Bigr)_{T,P}・・・(15)$$
$$\overline{m_{2}}=m-x_{1}\Bigl(\frac{∂m}{∂x_{1}}\Bigr)_{T,P}・・・(16)$$
(15)、(16)式となります。
最後に(15)式のx2をx1に変換します。
$$\frac{∂m}{∂x_{2}}=\frac{∂m}{∂x_{1}}\frac{∂x_{1}}{∂x_{2}}=\frac{∂m}{∂x_{1}}\frac{∂}{∂x_{2}}(1-x_{2})=-\frac{∂m}{∂x_{1}}・・・(17)$$
(17)式となりますので、最終的に
$$\overline{m_{1}}=m+(1-x_{1})\Bigl(\frac{∂m}{∂x_{1}}\Bigr)_{T,P}・・・(18)$$
$$\overline{m_{2}}=m-x_{1}\Bigl(\frac{∂m}{∂x_{1}}\Bigr)_{T,P}・・・(16)$$
(18)、(16)式が得られます。
この2式を縦軸m、横軸x1の関数として考えると、
$$m=-(1-x_{1})\Bigl(\frac{dm}{dx_{1}}\Bigr)+\overline{m_{1}}・・・(19)$$
$$m=x_{1}\Bigl(\frac{dm}{dx_{1}}\Bigr)+\overline{m_{2}}・・・(20)$$
(19)、(20)式となります。図示すると、
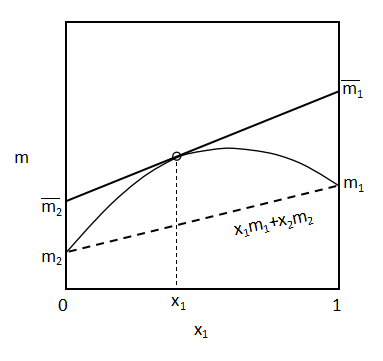
上図のようになります。
(19)、(20)式は状態量mを表わす曲線の点x1における接線となります。
加えて、x1=0のときの切片の値が部分モル量m2となり、x1=1のときの値が部分モル量m1となります。
部分モル量の具体例
部分モル体積
部分モル量のわかりやすい例として部分モル体積がよく挙げられます。
例えば1atm、25℃において水とエタノールを100cm3ずつ加えて混合したとすると、混合物の体積は200cm3にはならず約190cm3になります。
これは分子間に相互作用が働くのが要因で、ある分子に注目したときにその分子を囲むミクロな環境によって分子が占める体積が変化するためです。
純粋な水であれば1mol当たり約18cm3の体積増加となりますが、大量のエタノールに水を1mol加えたときの体積増加は約14cm3となります。
後者の場合、大量のエタノールに水を1mol加えても、液全体の組成はほぼ変化しないものと考えることができます。
このときの体積増加量は、部分モル量の定義である"水の成分だけを微小変化させたときの体積変化量"を意味しています。
したがって、体積増加量約14cm3はこのエタノール溶液における水の部分モル体積となります。
部分モル量を導入することで、このような混合物の物性変化を表現できるようになります。
部分モルギブス自由エネルギー
気液平衡などの物性計算で重要なのが部分モルギブス自由エネルギーです。
ギブス自由エネルギーも体積の例と同様で、1kJのギブス自由エネルギーを持つ物質であるAとBを混合したとしても、2kJのギブス自由エネルギーを持つ混合物にはなりません。
成分Aの部分モルギブス自由エネルギーは、温度T、圧力P、成分Bのモル量nB一定で、成分Aのモル量nAのみを微小変化させたときのギブス自由エネルギー変化量となりますから、
$$\overline{G_{A}}=(\frac{∂G}{∂n_{A}})_{T,P,n_{B}}・・・(21)$$
(21)式となります。(21)式を多成分系へと拡張すると、
$$\overline{G_{i}}=(\frac{∂G}{∂n_{i}})_{T,P,n_{j}(j≠i)}・・・(22)$$
(22)式となります。
(23)式は、実は化学ポテンシャルの定義と全く同じになります。
$$μ_{i}=\overline{G_{i}}・・・(23)$$
(23)式のように、化学ポテンシャルは部分モルギブス自由エネルギーと同義です。
したがって、化学ポテンシャルは多成分系におけるギブス自由エネルギーに関して、混合物の特性によるギブス自由エネルギー変化を加味して表現できる状態量となっています。
おわりに
部分モル量について解説しました。
混合物の状態量を組成平均値で表すための仮想的な量であることを覚えておきましょう。
