概要
蒸留塔では気液接触させる段数が多いほど分離が促進されますが、むやみに段数を増やすと蒸留塔が長くなりコストが高くなります。
そのため目標とする製品純度を達成するために、最低限どれだけの段数(理論段数)が必要かを求めることは非常に重要です。
この理論段数を作図で簡便に求める方法のことを、McCabe-Thiele(マッケーブ-シール)の階段作図(以下MT法)といいます。
この方法は蒸留塔の操作を図で表すことで、蒸留操作を直感的に理解できる点が非常に優れています。
その一方で、MT法は様々な仮定のもとで成り立っているため、実際の蒸留塔だとMT法で計算できない場合が多いです。
この記事ではMT法の作図方法について紹介します。
内容
MT法では主に連続式の蒸留塔が例に挙げられます。
連続式蒸留塔は下図に示すような形がスタンダードです。
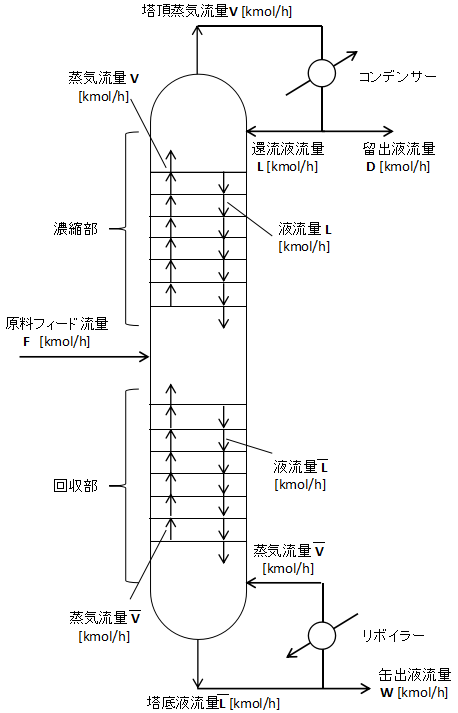
原料は塔の中段にフィードします。
(もちろん実際の蒸留塔では原料供給段がぴったり真ん中にあるとは限りません。)
原料供給段より上を濃縮部といいます。蒸留塔では製品を上から抜き出すことが多いため、製品を濃縮して純度を高める、という意味で濃縮部と呼ばれています。
原料供給段より下を回収部といいます。原料供給段より下に落ちていった製品をそのまま抜き出すとロスしてしまうので蒸留して回収する、という意味で回収部と呼ばれています。
McCabe-Thiele法の仮定
MT法では簡単に作図できるようにするために、以下の仮定をおいています。
液の顕熱差は無視する
塔内では上の段ほど温度が低く、下の段ほど温度が高いため温度分布が必ず存在します。
液の比熱は温度に依存性があるため、温度が違えば比熱の値も異なり、液の顕熱(液エンタルピー)は本来各段で異なるはずです。
なおかつ混合物の組成が変われば当然混合物の比熱も異なってきます。
しかし比熱の温度依存性、組成依存性を持たせると式が複雑になるため、塔内の液比熱は一定とし顕熱も一定とすることで簡略化しています。
各成分のモル蒸発潜熱は等しい
蒸発潜熱も比熱と同様に温度依存性、組成依存性があります。
これも塔内の蒸発潜熱を一定として簡略化しています。
ガスのエンタルピー = 液のエンタルピー + 蒸発潜熱
ガスのエンタルピーは上式で算出できます。
液のエンタルピーは仮定1で一定値としており、蒸発潜熱も仮定2で一定値としていますから、
要するにガスのエンタルピーも一定値となります。
各成分の混合熱は無視する
物質が混合した際には熱が発生し、これにより熱収支が変化します。
しかし蒸留塔では混合熱よりも蒸発潜熱の方が圧倒的に大きいので、混合熱の熱収支への寄与は微々たるもので、ほぼ無視できるでしょう。
塔壁からの熱損失は無視する
実際には塔壁から熱が逃げていますが、微々たるものでしょう。
熱損失を無視しても熱収支は大きく変わりません。
等モル流れ
上の4つの仮定を合わせると、塔内は等モル流れが成立します。
等モル流れとは、各段を流れる液とガスのモル流量が常に一定であることです。
言い換えれば液のモル流量Lとガスのモル流量Vの比である、L/Vが一定になるということです。
なぜ等モル流れの仮定が重要かというと、この後の作図方法で示す操作線の傾きがL/Vであり、一定値であれば操作線が直線となるからです。
ちなみに、実際の物質で等モル流れに近い系はRaoultの法則に従う理想溶液系です。
ベンゼン-トルエンなどの同族炭化水素が理想溶液に近いです。
作図方法
MT法の階段作図では、濃縮部と回収部それぞれで物質収支を立てて操作線の式を導きます。
濃縮部操作線の算出
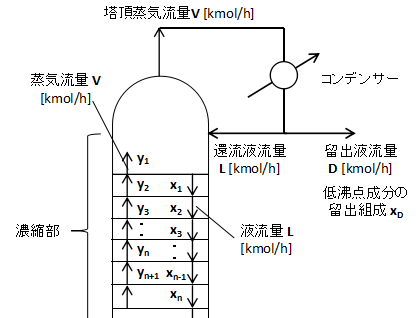
塔頂~濃縮部の拡大図を示します。
コンデンサー周りで物質収支を取ると、
$$V=L+D・・・(1)$$
(1)式となります。
また、塔頂に上ってくる低沸点成分について同様に物質収支を取ると、
$$Vy_{1}=Lx_{D}+Dx_{D}・・・(2)$$
(2)式となります。
(1)、(2)式が塔で最も濃縮している塔頂部の関係式です。
ただし、(1)、(2)式は塔頂のみを表わしており、その他の濃縮部がどうなっているかはわかりません。
そのため他の濃縮部についても式を立てます。
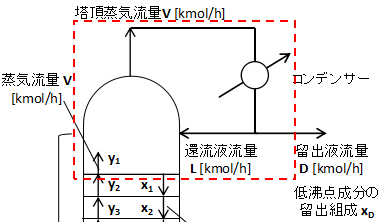
まず濃縮部1段目について式を立てます。
上図に1段目の物質収支を取るエリアを赤点線で示しています。
点線に流入流出する物質について収支を取ります。
等モル流れであるため、1段目から流出する液流量はL、1段目に流入するガス流量はVとなります。
したがって1段目での物質全体の収支は
$$V=L+D・・・(1)$$
(1)式となり、コンデンサー周りで取った収支と一致します。
同様に低沸点成分について物質収支を取ると、
$$Vy_{2}=Lx_{1}+Dx_{D}・・・(3)$$
(3)式となります。
続いて同じように濃縮部2段目について式を立てます。
物質全体の収支は、
$$V=L+D・・・(1)$$
同様に(1)式となります。
低沸点成分についての物質収支は、
$$Vy_{3}=Lx_{2}+Dx_{D}・・・(4)$$
(3)式となります。
ここまでくると傾向が見えてきましたね。
(2)、(3)、(4)の式はyとxに関する漸化式として表すことができます。
濃縮部n段について式を立てると、
$$Vy_{n+1}=Lx_{n}+Dx_{D}・・・(5)$$
(5)式となり任意の段nについて成り立ちます。
(5)式の両辺をVで割ると、
$$y_{n+1}=\frac{L}{V}x_{n}+\frac{D}{V}x_{D}・・・(6)$$
(6)式となります。
(6)式が濃縮部操作線の式となります。
ちなみに、(6)式を還流比Rで整理することもできます。
$$R=\frac{L}{D}・・・(7)$$
還流比Rは(7)式で表されます。
(6)式に(1)式を代入し式変形すると、
$$y_{n+1}=\frac{L}{L+D}x_{n}+\frac{D}{L+D}x_{D}$$
$$y_{n+1}=\frac{L/D}{L/D+1}x_{n}+\frac{1}{L/D+1}x_{D}$$
(7)式の還流比Rで表すと、
$$y_{n+1}=\frac{R}{R+1}x_{n}+\frac{1}{R+1}x_{D}・・・(8)$$
(8)式となり、還流比Rと塔頂組成xDがわかれば濃縮部操作線の式を書くことができます。
回収部操作線の算出
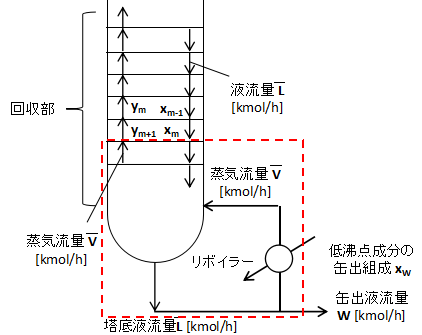
上図に塔底付近の拡大図を示します。
リボイラー周りで物質収支を取ると、
$$\bar{L}=\bar{V}+W・・・(9)$$
(9)式となります。
また、塔底に降りてくる低沸点成分について、任意の段mで赤点線部分の物質収支を取ると、
$$\bar{L}x_{m}=\bar{V}y_{m+1}+Wx_{W}$$
$$y_{m+1}=\frac{\bar{L}}{\bar{V}}x_{m}-\frac{W}{\bar{V}}x_{W}・・・(10)$$
(10)式となります。
(10)式が回収部操作線となります。
q線の算出
濃縮部と回収部については(6)、(10)式で計算できるようになりましたが、もう1つ塔内で重要な因子があります。
それが原料供給段です。
原料供給段は階段作図とともにq線を作図することで求めることができます。
q線とは、濃縮部操作線(6)式と回収部操作線(10)式の交点の軌跡を示す式です。
濃縮部と回収部が一致する点を表わしているため、原料供給段について物質収支及び熱収支を取ることで導出できます。

上図に原料供給段の図を示します。
原料供給段で物質収支を取ると、
$$F+L+\bar{V}=\bar{L}+V$$
$$V-\bar{V}=F+L-\bar{L}・・・(11)$$
(11)式となります。
続いて熱収支を取ると、
$$Fh_{F}+Lh+\bar{V}H=\bar{L}h+VH$$
$$Fh_{F}=(V-\bar{V})H-(L-\bar{L})h・・・(12)$$
hF:原料のエンタルピー、H:ガスのエンタルピー、h:液のエンタルピー
(12)式となります。
実際には各段で液・ガスのエンタルピーは異なりますが、前述したMT法の仮定により全ての段で液・ガスのエンタルピーが等しいとして扱えます。
(12)式に(11)式を代入し変形した形がq値になります。
$$Fh_{F}=(F+L-\bar{L})H-(L-\bar{L})h$$
$$F(H-h_{F})=(\bar{L}-L)(H-h)$$
$$q=\frac{\bar{L}-L}{F}=\frac{H-h_{F}}{(H-h)}・・・(13)$$
(13)式から、
$$Fq=\bar{L}-L・・・(14)$$
(14)式が成り立ちます。
また、(14)式を(11)式に代入すると、
$$V-\bar{V}=F(1-q)・・・(15)$$
(15)式が得られます。
これら(14)、(15)式を濃縮部操作線(6)式と回収部操作線(10)式を連立させた式に代入することでq線の方程式を得ることができます。
(6)式と(10)式を下に示します。
ただし、連立させて交点をもとめるために添え字を外します。
(任意の段について成り立つためy、xの添え字を外しても問題ありません。)
$$y=\frac{L}{V}x+\frac{D}{V}x_{D}・・・(6)'$$
$$\bar{L}x=\bar{V}y+Wx_{W}・・・(10)'$$
(6)'、(10)'を連立させて整理すると、
$$(V-\bar{V})y=(L-\bar{L})x+(Dx_{D}+Wx_{W})・・・(16)$$
(16)式となります。

ここで上図の赤点線ように塔全体で低沸点成分について物質収支を取ります。
$$Fz_{F}=Dx_{D}+Wx_{W}・・・(17)$$
(14)、(15)、(17)式を(16)式に代入します。
$$F(1-q)y=-Fqx+Fz_{F}$$
$$y=-\frac{q}{1-q}x+\frac{z_{F}}{1-q}・・・(18)$$
この(18)式がq線の方程式になります。
この式を作図するうえでの特徴は、
・濃縮部操作線(6)式と回収部操作線(10)式の交点をq線も通る
・点(zF,zF)を通る
上に示すものがあります。
直線は2点わかれば引けるので、上の2点を利用してq線を作図するのがよいでしょう。
また、余談ですがq値はフィードする原料の状態を表わしており、
・q=1:沸点の液
・0<q<1:気液混相
・q=0:沸点の蒸気
上の3種類に分かれます。
どの状態が良いかは一概に言えません。
ただ、少なくとも原料を加熱せずにフィードするよりは、加熱してフィード液を沸点近くまで上昇させてフィードする方が分離効率は良くなります。
そのため、蒸留塔の前には予熱器が設置されていることがよくあります。
気液平衡曲線の算出
気液平衡曲線を作図する最も簡単な方法は、2成分の気液平衡データをxy線図にプロットして自分で曲線を引くことです。
例えば大学の筆記テストでは問題で気液平衡データが与えられ、自分で点をプロットして曲線を引くことをやったことがあります。
テストレベルの話であればそれでもよいでしょう。
しかしフリーハンドで曲線を引くと個人差が出てくるので、なるべくエクセルに曲線を引かせたいところです。
そのために気液平衡曲線の式を導出します。
xy線図の気液平衡曲線は、相対揮発度の関係式から導出することができます。
-

【相対揮発度(比揮発度)】を解説:蒸留分離のしやすさを示す指標
ある2成分がどれだけ蒸留分離しやすいのかを示す指標を相対揮発度、もしくは比揮発度といいます。相対揮発度αABがわかれば気液平衡曲線が書けるため、蒸留において重要な指標と言えます。
続きを見る
詳しくは上の相対揮発度の記事に記載しています。
気液平衡曲線は、
$$y_{A}=\frac{α_{AB}x_{A}}{(α_{AB}-1)x_{A}+1}・・・(19)$$
αAB:相対揮発度
(19)式で表されます。
(19)式から、相対揮発度がわかれば気液平衡曲線が書けることがわかります。
相対揮発度はRaoultの法則が成り立つ理想溶液であれば、
$$相対揮発度α_{AB}=\frac{P_{A}}{P_{B}}・・・(20)$$
PA:成分Aの蒸気圧、PB:成分Bの蒸気圧
(20)式のように各成分の純物質の蒸気圧から算出できます。
蒸気圧の算出方法については
-

【純物質の蒸気圧】推算方法を解説:Antoine式が精度高い
蒸気圧とは気体と液体が平衡関係にある場合の気相の圧力のことで、化学プラントの装置設計においては非常に重要な物性です。特に蒸留塔のような2成分以上の混合物の気液平衡を扱う場合に、まず純物質の蒸気圧を算出する必要があります。
続きを見る
上の記事で記載しています。
純物質の蒸気圧は基本的にAntoine式で算出することが多いです。
Antoine式のパラメータは文献等を参照します。
作図
濃縮部操作線、回収部操作線、q線、気液平衡曲線の式がわかれば、いよいよ作図することができます。
まずはy=xの線と気液平衡曲線を作図しましょう。

一般的にMT法で作図する場合は理想溶液に近い系であることが多いです。
理想溶液系であれば上図のような青色の気液平衡曲線になるはずです。
ちなみにどんな種類の気液平衡曲線があるのかはこちらの記事で解説しています。
-

【xy線図】を特徴的な2成分系ごとに解説:液相・気相の関係図
ある2成分の気液平衡関係を表わすグラフのことをxy線図といいます。2成分のうち沸点が低い方をプロットするのが蒸留分野の慣習となっています。
続きを見る
続いて濃縮部操作線と回収図操作線を作図します。
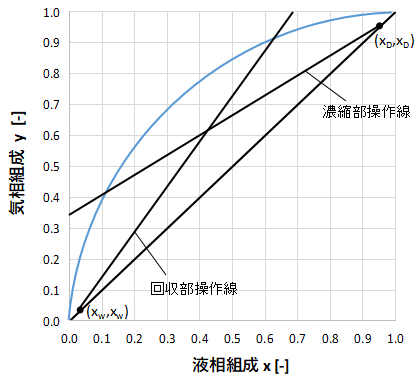
上図のように2つの直線を引いて作図上で交点を求めるのも良いですが、交点がずれることもあります。

事前に濃縮図操作線と回収部操作線の式を連立させて解き、交点の座標を求めておけば作図も楽になります。
また、濃縮部操作線は点(xD,xD)、回収部操作線は点(xW、xW)を通ることが(6)、(10)式からわかりますから、作図のときに利用すると楽に線を引けます。
続いて階段を作図していきます。
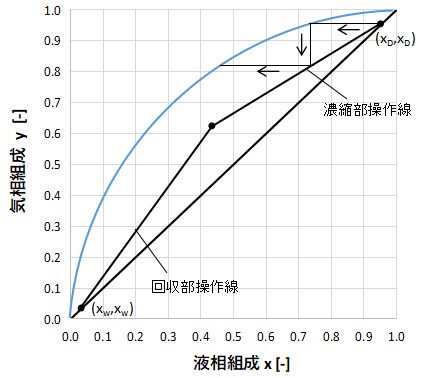
最初は塔頂の(xD,xD)からスタートします。
(xD,xD)から左側へ真横に直線を引き、気液平衡曲線と交わるところで止めます。
次にこの交点から真下に直線を引き、濃縮部操作線と交わるところで止めます。
次にまた左側へ真横に直線を引き・・・という操作を繰り返します。
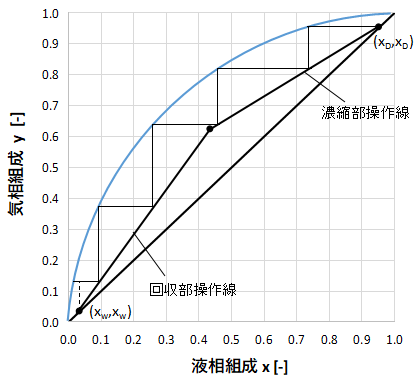
最後は上図のようにx=xwを過ぎたところで終了します。
理論段数の算出
作図が終われば階段の段数を数えます。
この階段数が理論段数を表わしています。

上図だと、きれいに段になっているのが4段で、最後の1段はx=xwをまたいでいますね。
この場合は線分の比を取ります。
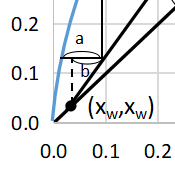
5段目の線の長さをa、回収部操作線からx=xwまでの距離をbとすると最後の段で有効な段数は
$$有効段=\frac{b}{a}$$
となります。
今回の例の場合は、有効段=0.75段となります。
よって、階段数を合計すると4+0.75=4.75段となります。
ただし通常、理論段数はこの階段数から1を引いた値となります。
塔底にはリボイラーが設置してあり、塔内の段数とは別に理論段数1段分の分離効果があるためです。
(余談ですが、実際はリボイラーの種類によって理論段数1段分の効果がないものもあります。)
まとめると、今回の例では
$$理論段数=階段数-1=4.75-1=3.75段$$
となりました。
実際の設計では3.75段は切り上げて理論段数4段として計算します。
原料供給段の算出
階段作図したグラフにq線を書くことで最適な原料供給段を算出できます。
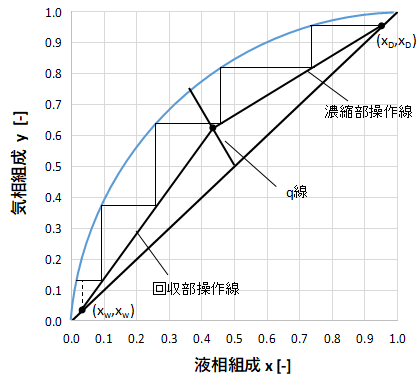
例えば上図のようにq線が引けた場合はq線が3段目で交わっているため、最適な原料供給段は3段となります。
ただしあくまでも作図の精度なので、本当に3段で良いかどうかはシミュレータ等で蒸留計算して確かめた方がよいでしょう。
原料供給段が最適な位置からずれていると、分離性能が悪化したり分離に余計なエネルギーが必要になります。
古いプラントでは度重なる増強や改造に伴い運転条件が変化し、最適な原料供給段が当初の設計からずれることがあります。
そのようなプラントで原料供給段を適正化すれば大きな省エネが見込めますので検討する価値はあるかと思います。
まとめ
・McCabe-Thiele(マッケーブ-シール)の階段作図は蒸留の概念を図で理解することができる優れた作図法です。
・ただし様々な仮定を置いているため、実際の系とは合わないことがよくあります。
・精度良く蒸留計算したければシミュレータを使用するのがよいでしょう。



