概要
過剰量は実在混合物と理想混合物の状態量の差として定義されています。
$$m^{E}=m-m^{id}・・・(1)$$
mE:過剰量、m:実在混合物の状態量、mid:理想混合物の状態量
気液平衡を計算するための活量係数モデルでは、過剰量が大いに関係しており重要な概念です。
本記事では過剰量について解説しています。
定義
過剰量の前に、理想混合物について理解すべきです。
ここでは、過剰量で最もよく議論されるギブス自由エネルギーを状態量として解説します。
理想混合物の定義
まず理想混合物のギブス自由エネルギーの混合量Δgidを求めてみましょう。
ギブス自由エネルギーの基礎式から、
$$dg=VdP-SdT・・・(2)$$
(2)式が成立します。
次に、理想気体の状態方程式が成り立つものとします。
$$PV=RT・・・(3)$$
(3)式を(2)式に代入し、
$$d{g_{i}}^{id}=\frac{RT}{P}dP-SdT・・・(4)$$
(4)式となります。(4)式を温度一定下で圧力P0~Pまで積分します。
$${g_{i}}^{id}(T,P)={g_{i}}^{id}(T,P^{0})+RT{\rm{ln}}\frac{P}{P^{0}}・・・(5)$$
(5)式が得られます。
(5)式について、全圧Pの代わりに分圧piを使用すると、混合物中の成分iの部分モルギブス自由エネルギーが得られます。
$$\begin{align}{\bar{g_{i}}}^{id}(T,P)&={g_{i}}^{id}(T,P^{0})+RT{\rm{ln}}\frac{p_{i}}{P^{0}}\\&={g_{i}}^{id}(T,P^{0})+RT{\rm{ln}}\frac{P}{P^{0}}+RT{\rm{ln}}y_{i}\\&={g_{i}}^{id}(T,P)+RT{\rm{ln}}y_{i}・・・(6)\end{align}$$
したがって、ギブスの自由エネルギーの混合量Δgidは部分モル量の定義から、
$$\begin{align}Δg^{id}&=\sum y_{i}({\bar{g_{i}}}^{id}-g^{id})\\&=RT\sum y_{i}{\rm{ln}}y_{i}・・・(7)\end{align}$$
(7)式のように表すことができます。
ちなみに、Δgidは0≦yi≦1であることから、常に負の値を示すことがわかります。
過剰量の定義
(1)式をギブス自由エネルギーの混合量Δgについて適用すると、
$$Δg=Δg^{id}+g^{E}・・・(8)$$
(8)式となります。
Δgidは(7)式で算出することができます。
過剰ギブス自由エネルギーgEについては、化学ポテンシャルと活量係数の定義である(9)式から導かれます。
$${μ_{i}}^{E}={\bar{g_{i}}}^{E}=RT{\rm{ln}}γ_{i}・・・(9)$$
部分モル量の定義から組成を液相基準にすると、
$$g^{E}=\sum x_{i}{\bar{g_{i}}}^{E}=RT\sum x_{i}{\rm{ln}}γ_{i}・・・(10)$$
(10)式でgEを表わすことができます。
ΔgidとgEから実際の混合量Δgを計算することができます。
計算例
例として、20℃(293.15K)一定下でのメタノール-水系のΔgを計算してみましょう。
ただし、活量係数が以下の表で与えられているとします。
メタノールの モル組成x1[-] | メタノールの 活量係数γ1 | 水の 活量係数γ2 |
| 0.00 | 1.4521 | 1.0000 |
| 0.05 | 1.4866 | 0.9995 |
| 0.10 | 1.4966 | 0.9991 |
| 0.20 | 1.4171 | 1.0097 |
| 0.30 | 1.2856 | 1.0426 |
| 0.40 | 1.1836 | 1.0909 |
| 0.50 | 1.1028 | 1.1524 |
| 0.60 | 1.0512 | 1.2229 |
| 0.70 | 1.0207 | 1.2924 |
| 0.80 | 1.0060 | 1.3511 |
| 0.90 | 1.0007 | 1.3912 |
| 1.00 | 1.0000 | 1.4009 |
"化学技術者のための実用熱力学演習"より引用
まず、Δgidは(7)式から求めることができます。
ただ、(7)式は気相基準であるのに対して、今回の系は液相であるため、気相組成yiを液相組成x1に修正した(11)式を使用しましょう。
$$Δg^{id}=RT(x_{1}{\rm{ln}}x_{1}+x_{2}{\rm{ln}}x_{2})・・・(11)$$
次にgEは(10)式から求めることができます。
最後に(8)式を使用してΔgidとgEを足せばΔgを求めることができます。
注意点として、x1=0、x2=0のΔgidは対数があるため(11)式で直接計算できませんが、理論上純物質のΔgidはゼロとなります。
算出したΔgid、gE、Δgを下図に示します。
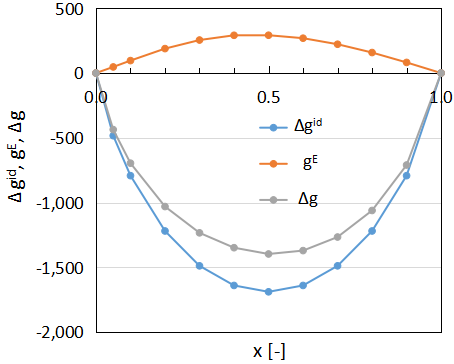
Δgidが常にマイナスの値となる一方で、gEはプラスにもマイナスにもなり得るパラメータです。
また、どちらかの組成が小さいとΔgid、gE、Δgはゼロに近くなります。
このように理想混合物の状態量midを過剰量mEで補正することで、実際の状態量mを算出することができます。
おわりに
過剰量について解説しました。
実在混合物の状態量と理想混合物の状態量の差で定義されています。
理想部分と実在部分に分けて考えることで、学問的に取り扱いしやすくなりました。
