概要
気液撹拌はガス吸収や化学反応、あるいは発酵などの目的で行われます。
撹拌槽への気体の供給方法によって大きく3種類に分けることができます。
- 浸漬撹拌式:撹拌翼を槽底付近に設置し、ノズル・リングスパージャーでガスを供給し液中に分散させる
- 表面撹拌式:撹拌翼を液面付近に設置し、液面からガスを巻き込み液中に分散させる
- 自己吸引撹拌式:撹拌翼の吸引作用を利用して、液面上のガスを撹拌軸に沿って翼まで吸引して分散させる
どの手法も一長一短はありますが、液中全体にガスを分散させやすい浸漬撹拌式が採用されやすい印象です。
本記事では浸漬撹拌式の気液撹拌について、気泡の分散状態や撹拌動力について解説します。
気泡の分散状態の変化
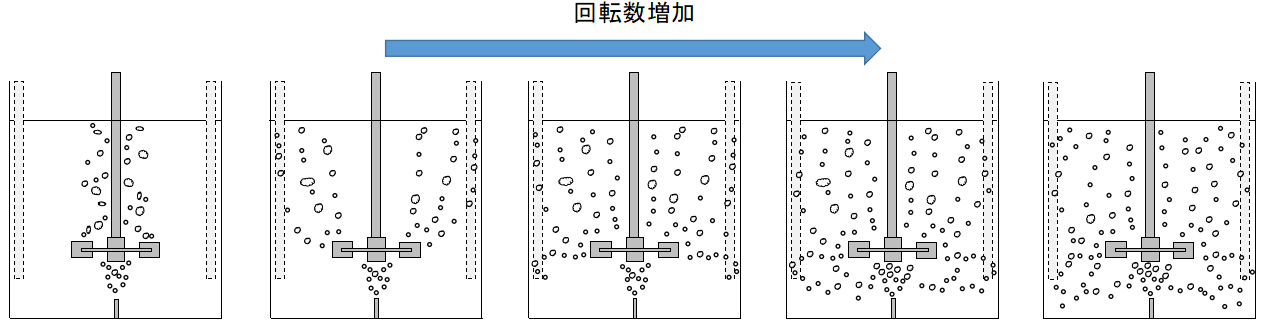
撹拌槽内にガスを供給すると撹拌翼の吐出により槽内へ分散しますが、その度合いは通気量や撹拌回転数に依存します。
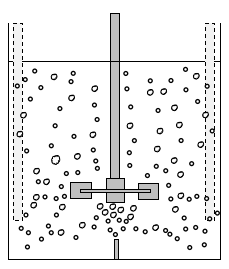
仮に翼の真下からガスを通気量一定で供給する場合に、撹拌回転数を増加させていくと以下の5つの分散状態へと変化していきます。
(a)フラッディング
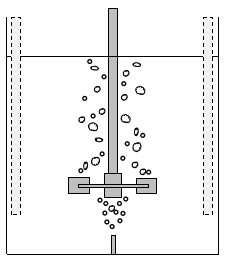
撹拌翼が停止している、あるいは低回転数だとガスは撹拌軸の周りに沿って巻くように上昇します。
このようにガスが分散せずにそのまま上に吹き抜ける状態をフラッディングといいます。
(蒸留にもフラッディングという用語がありますが、意味合いが少し違うので注意しましょう。)
気液接触の効率は悪く、フラッディング状態では気液撹拌の目的を達成することは困難でしょう。
撹拌動力は無通気時の動力とほとんど変わりません。
(b)槽内への気泡分散
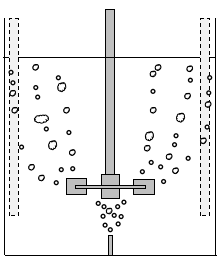
回転数を増加させると気体は撹拌翼の吐出による影響を受け、徐々に槽内に分散していきます。
ただしこの状態では撹拌よりも通気の影響の方が大きいため、不十分な分散状態です。
また、撹拌翼の後方に気体の空洞が形成され始めるため、回転数の増加に伴い撹拌動力は徐々に低下していきます。
アカデミックの分野では、特にディスクタービン翼後方に形成される気体の空洞について様々な研究がなされています。
(c)槽上部全域への気泡分散
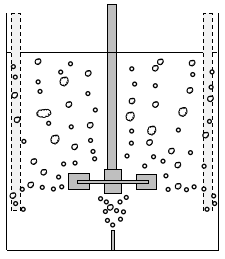
さらに回転数を増加させると、供給された全てのガスが翼の吐出流によって槽上部全域に分散します。
この状態をローディングといいます。
撹拌動力はローディングに近い状態の回転数で最小となります。
Nienowらは
- 6枚ディスクタービン翼
- H(液高さ)=D(槽径)
- C(翼の設置高さ)=D/4
のときの撹拌動力が最小となる回転数NCD[1/s]の推算式を発表しています。
単一孔スパージャーのとき、
$$N_{CD}=4{Q_{G}}^{0.5}D^{0.25}/d^{2}・・・(1)$$
リングスパージャーのとき、
$$N_{CD}=3{Q_{G}}^{0.5}D^{0.25}/d^{2}・・・(2)$$
QG:通気ガス流量[m3/s]
"化学工学の進歩24 攪拌・混合"より引用
となります。
(d)槽下部での気泡循環

さらに回転数を増加させると、槽下部で形成されている循環流に翼から吐出された小さな気泡が追随するようになります。
槽上部だけでなく槽下部も気液接触するため、一般的にこの状態が最適な気泡の分散状態とされています。
実用上は動力が最小となる回転数NCDと動力が最大となる回転数NRを推算し、NCD<N<NRとなる回転数を設定することで効率の良い気液撹拌を行なうことができます。
また、この状態では通気よりも撹拌による影響が大きく、回転数を増加させると撹拌動力は増加します。
(e)槽上部での気泡循環
さらに回転数を増加させると、完全に撹拌が支配的となり槽上部の循環流に気泡が追随するようになります。
気液の物質移動の観点から言うと、かけた動力に対して物質移動係数の向上がそれほど見られません。
撹拌動力はこの状態に近い回転数で最大となります。
同様にNienowらは撹拌動力が最大となる回転数NR[1/s]の推算式(3)を発表しています。
$$N_{R}=1.5{Q_{G}}^{0.2}D/d^{2}・・・(3)$$
通気時の撹拌動力
通気時の撹拌動力は無通気時とは違い、独特の挙動を示しますので予測しづらいです。
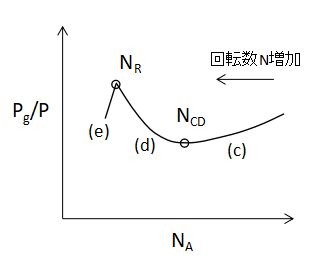
上図に通気ガス流量QGが一定の時の動力曲線を示します。縦軸に通気時撹拌動力Pgと無通気時撹拌動力Pとの比を取り、横軸に通気係数NAを取ります。
通気係数NAは
$$N_{A}=\frac{Q_{G}}{Nd^{3}}・・・(4)$$
QG:通気ガス流量[m3/s]、d:翼径[m]
(4)式で表される無次元数です。
QGが一定の場合、回転数Nが増加すると横軸NAの値は減少します。
このとき縦軸Pg/Pは、
(c)領域:回転数Nの増加に伴い減少し、回転数NCDで最小値を示す
(d)領域:回転数Nの増加に伴い増加
(e)領域:回転数NRで最大値を示す
以上のような傾向を示します。あくまでも傾向であり、実測してみるとこれほどはっきりと傾向が出ないこともあります。
また、通気時の撹拌動力Pgの相関式が様々発表されており、ここではその一部を紹介します。
$$\frac{P_{g}}{P}=0.10(\frac{Q_{G}}{NV})^{-1/4}(\frac{N^{2}d^{4}}{gbV^{2/3}})^{-1/5}・・・(5)$$
"化学工学の進歩24 攪拌・混合"より引用
V:液体積[m3]、g:重力加速度[m/s2]、b:羽根幅[m]
$$\frac{P_{g}}{P}=0.157(\frac{Q_{G}^{0.44}}{P^{0.22}N_{A}})^{0.45}・・・(6)$$
"工業反応装置"より引用
スケールアップ
kLa一定
気液撹拌の目的によってどのようなパラメータをスケールアップの指標にするかは異なってきます。
しかし最もよくある指標の1つが液相側物質移動容量係数kLaを一定とするスケールアップです。
kLaの記事でも解説しましたが、一般に
$$k_{L}a=α{P_{V}}^{β}{u_{g}}^{γ}・・・(7)$$
PV:単位液量当たりの撹拌動力[W/m3]、ug:ガス線速度[m/s]
(7)式の関係が成り立つとされています。
したがって、ガス線速度ug一定、単位体積当たりの撹拌動力PV一定とすればをkLa一定とすることができます。
VVM一定
気液撹拌では容量当たりの生産性を同一にするために、単位液量当たりの通気量VVM一定でスケールアップすることもよくあります。
$$\frac{Q_{G}[m^{3}/min]}{V[m^{3}]}=[vvm]・・・(8)$$
このときスケールアップ前後では、
$$\frac{Q_{G1}}{V_{1}}=\frac{Q_{G2}}{V_{2}}・・・(9)$$
QG1,QG2:スケールアップ前後の通気量[m3/min]
V1,V2:スケールアップ前後の液量[m3]
(9)式が成り立ちます。
ここで、通気量QGとガス線速度ugには
$$Q_{G}={\frac{πD}{4}}^{2}・u_{g}・・・(10)$$
D:槽径[m]
(10)式が成り立ちます。(10)式を(9)式に代入すると、
$$\frac{{D_{1}}^{2}u_{g1}}{V_{1}}=\frac{{D_{2}}^{2}u_{g2}}{V_{2}}・・・(11)$$
(11)式となります。
仮に相似形のスケールアップだとすると、
$$V≒D^{3}・・・(12)$$
(12)式が成り立ちます。(12)式を(11)式に代入し、
$$\frac{{D_{1}}^{2}u_{g1}}{{D_{1}}^{3}}=\frac{{D_{2}}^{2}u_{g2}}{{D_{2}}^{3}}$$
$$u_{g2}=\frac{D_{2}}{D_{1}}u_{g1}・・・(13)$$
(13)式となります。
D2/D1はスケールアップだと必ず1より大きいので、VVM一定でスケールアップするとガス線速度ugの値は増加します。
また、(7)式から、
$$k_{L}a=α{P_{V}}^{β}{u_{g}}^{γ}・・・(7)$$
VVM一定スケールアップ時にkLaも一定にしようとすると、ugが大きくなるぶんPVを小さくしなければなりません。
したがって、VVM一定スケールアップは撹拌に対して通気の影響が相対的に大きくなりやすく、ガス分散の不足が起こりやすいです。
通気量に負けないように撹拌回転数を増加させる、翼径を大きくするなどの対策が有効です。
おわりに
気液撹拌について解説しました。
液液撹拌、固液撹拌に比べて気液撹拌は密度差が大きいので分散させにくいです。
気液反応槽のような生産性に大きくかかわる装置の設計ではラボで気液分散状態をしっかり確認してからスケールアップしましょう。
