【Python】Runge-Kutta法の計算例：回分式反応器の一次反応

概要

本記事ではPythonでの化学工学計算例を紹介しています。今回はRunge-Kutta法を使用して、回分式反応器の一次反応による原料濃度変化を計算します。

まずは簡単な一次反応に関するPythonの記述方法をマスターしておけば、より複雑な反応にも応用できるようになるでしょう。

計算式

今回計算する式は以下の記事で解説したものを使用します。

: 【Runge-Kutta法】をわかりやすく解説：Euler法より精度の良い数値解法
Runge-Kutta法(ルンゲクッタ法)は常微分方程式を解く手法の1つです。本記事ではRunge-Kutta法の計算手法について解説します。加えて、回分式反応器の一次反応に関する例題を解いてみて、Euler法とRunge-Kutta法の計算精度を比較してみました。

この記事ではExcelを使用してRunge-Kutta法で解いていますが、今回は同じ式をPythonで解いてみます。

計算結果の比較のため、Euler法もPythonで計算して結果を出力してみます。

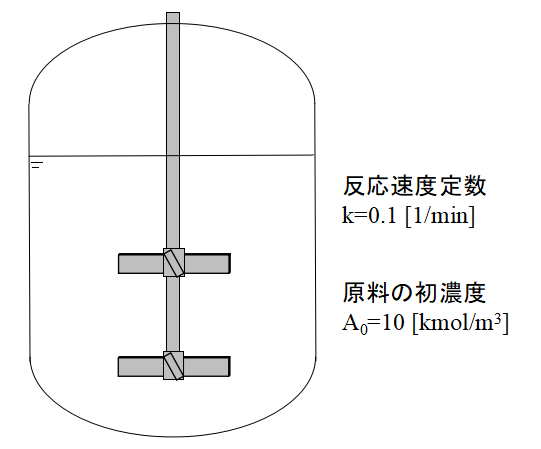
反応速度定数k：0.1[1/min]
原料の初濃度：10[mol/L]

t=10minまで計算し、Euler法の結果と比較しましょう。

$$\frac{dA}{dt}=-kA・・・(1)$$

回分式反応器の一次反応の計算式は(1)式で表され、(1)式をRunge-Kutta法で解いていきます。

Python記述

ライブラリ・モジュールのインポート

今回はEuler法の結果とRunge-Kutta法の結果をPython上でグラフにして比較してみましょう。

Pythonでグラフを作成するときは、Matplolibというライブラリを使用します。

#Matplolibインポート
import matplotlib.pyplot as plt

ただ、matplotlibと各行に毎回書くのは少し面倒ですね。

語尾にas pltと付け加えることで、pltと略して記述することができます。

前提条件の入力

次に問題で与えられる前提条件を入力します。

今回は反応速度定数kを入力します。

#前提条件
k=0.1  # 1/min

初期条件の入力

次に初期条件が必要な場合はその値を入力します。

今回は原料濃度の初期値と時間の初期値としてt=0を入力します。

#初期条件
A=10  # mol/L
t=0  # min

その他計算条件の入力

今回は時間刻みhと繰り返し計算回数imaxを入力します。

#その他計算条件
h=1  # min
imax=11  # 計算回数の指定

時間刻みはh=1としました。

また、for文を使って繰り返し計算を行なう予定なので、繰り返し計算回数をimaxとして入力します。

imax=11としました。時間tを1min刻みで0～10minまで計算するわけなので、繰り返し回数は11回となります。

グラフ作成用の配列設定

次にグラフ作成用の空の配列を作成します。

#グラフ作成用
gt = []
gAE = []
gAR = []

gtは時間tを入れるための空の配列です。

gAE、gARはそれぞれEuler法とRunge-Kutta法の濃度Aの計算結果を入れるための空の配列です。

配列名は別になんでもよいですが、なるべくわかりやすい名前を付けましょう。

方程式の定義

次にメインの方程式を定義します。

今回もdefとreturnで(1)式を定義します。

#方程式定義
def fA(A):
    return -k*A

(1)式の左辺dA/dt=fA(A)とし、右辺をreturnで計算値が返ってくるように入力します。

Runge-Kutta法の入力

続いて Runge-Kutta 法を入力していきます。基本的な入力方法はEuler法で解説したものとほぼ同じですので被るところは省略します。

今回もfor文を使用して繰り返し計算を入力します。

#Runge-Kutta法
for i in range(imax):
    print('i:{0:4}, t:{1:5.1f}, A:{2:7.3f}' .format(i,t,A))  
    
    gt.append(t)
    gAR.append(A)

    k1=h*fA(A)
    k2=h*(-k*(A+k1/2))
    k3=h*(-k*(A+k2/2))
    k4=h*(-k*(A+k3))

    A=A+h*(k1+2*k2+2*k3+k4)/6  #()式
    t=t+h  # 時間tの更新

5,6行目にグラフ用に作成した空の配列に計算値を入力するコードを入力しています。

5行目はgtの配列に時間tを、6行目はgARの配列に濃度Aが入るよう入力します。

続いて8行目にRunge-Kutta法で必要なk₁～k₄の算出式を入力します。

$$k_{1}=hf(x_{n},y_{n}) ・・・(2) $$

$$k_{2}=h×f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{1}}{2})・・・(3) $$

$$k_{3}=h×f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{2}}{2})・・・(4) $$

$$k_{4}=h×f(x_{n}+h,y_{n}+k_{3})・・・(5) $$

k₁～k₄はRunge-Kutta法の記事で解説していますが、それぞれ(2)～(5)式で表されます。

次に13行目で濃度A値を更新しています。

$$ y_{n+1}=y_{n}+\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}・・・(6) $$

(6)式に従って、 k₁～k₄ の平均値を取ります。

最後に14行目で時間tを更新します。

初期条件のリセット

Runge-Kutta法の計算は終了したので、続いてEuler法でも計算します。

しかしこのままだとRunge-Kuttaの計算結果が時間tと濃度Aの初期値になってしまうため、一旦リセットします。

#初期条件リセット
A=10  # mol/L
t=0  # min

Euler法の入力

続いてEuler法の入力をします。詳しくはこちらの記事で説明しているため割愛します。

#Euler法
for i in range(imax):
    print('i:{0:4}, t:{1:5.1f}, A:{2:7.2f}' .format(i,t,A))  
    
    gAE.append(A)

    A=A+h*fA(A)  #Euler法
    t=t+h  #時間tの更新

グラフの出力

最後にグラフの出力に関するコードを記入します。

#グラフ出力
plt.plot(gt, gAE)
plt.plot(gt, gAR)
plt.xlabel('t [min]')
plt.ylabel('A [mol/L]')
plt.legend(['Euler', 'Runge-Kutta'])
plt.show()

2,3行目でグラフに出力する配列を入力します。

plt.plotの括弧内は(横軸x,縦軸y)の順に記入します。

今回は横軸を時間tの配列gt、縦軸を濃度Aの配列gAE、gARとしています。

4行目にx軸のラベルを入力しています。ラベルはt [min]とします。

5行目にy軸のラベルを入力しています。ラベルはA [mol/L]とします。

6行目に凡例を入力します。凡例はプロットした順に名前が付きますので、'Euler'、'Runge-Kutta'の順に入力します。

7行目でplt.show()としてグラフを出力します。

計算結果の確認

特に入力ミス等がなければ計算結果が以下のように表示されます。


i:   0, t:  0.0, A: 10.000
i:   1, t:  1.0, A:  9.048
i:   2, t:  2.0, A:  8.187
i:   3, t:  3.0, A:  7.408
i:   4, t:  4.0, A:  6.703
i:   5, t:  5.0, A:  6.065
i:   6, t:  6.0, A:  5.488
i:   7, t:  7.0, A:  4.966
i:   8, t:  8.0, A:  4.493
i:   9, t:  9.0, A:  4.066
i:  10, t: 10.0, A:  3.679
i:   0, t:  0.0, A:  10.00
i:   1, t:  1.0, A:   9.00
i:   2, t:  2.0, A:   8.10
i:   3, t:  3.0, A:   7.29
i:   4, t:  4.0, A:   6.56
i:   5, t:  5.0, A:   5.90
i:   6, t:  6.0, A:   5.31
i:   7, t:  7.0, A:   4.78
i:   8, t:  8.0, A:   4.30
i:   9, t:  9.0, A:   3.87
i:  10, t: 10.0, A:   3.49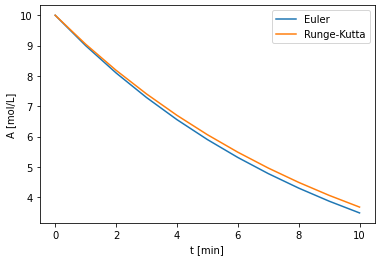

計算結果の数字とグラフが両方表示されます。計算結果の最初のi=0～10はRunge-Kutta法の結果で、次のi=0～10はEuler法の結果が出力されています。

グラフはちゃんと設定した通りにラベルや凡例付きで表示されていますね。

下に計算コードを最初から最後までまとめて載せておきます。

#Matplolibインポート
import matplotlib.pyplot as plt

#前提条件
k=0.1  # 1/min

#初期条件
A=10  # mol/L
t=0  # min

#その他計算条件
h=1  # min
imax=11  # 計算回数の指定

#グラフ作成用
gt = []
gAE = []
gAR = []

#方程式定義
def fA(A):
    return -k*A

#Runge-Kutta法
for i in range(imax):
    print('i:{0:4}, t:{1:5.1f}, A:{2:7.3f}' .format(i,t,A))  
    
    gt.append(t)
    gAR.append(A)

    k1=h*fA(A)
    k2=h*(-k*(A+k1/2))
    k3=h*(-k*(A+k2/2))
    k4=h*(-k*(A+k3))

    A=A+h*(k1+2*k2+2*k3+k4)/6  #()式
    t=t+h  # 時間tの更新 

#初期条件リセット
A=10  # mol/L
t=0  # min

#Euler法
for i in range(imax):
    print('i:{0:4}, t:{1:5.1f}, A:{2:7.2f}' .format(i,t,A))  
    
    gAE.append(A)

    A=A+h*fA(A)  #Euler法
    t=t+h  #時間tの更新 

#グラフ出力
plt.plot(gt, gAE)
plt.plot(gt, gAR)
plt.xlabel('t [min]')
plt.ylabel('A [mol/L]')
plt.legend(['Euler', 'Runge-Kutta'])
plt.show()

ライブラリの使用

Runge-Kutta法はライブラリを使用することで簡便に計算できるようです。

私も詳細までは理解しきれていませんが、scipyのodeintはRunge-Kutta法とほぼ同じ計算ができるようです。

計算コードを下に示します。

#scipy、numpyインポート
from scipy.integrate import odeint
import numpy as np

#前提条件
k=0.1  # 1/min

#初期条件
A=10  # mol/L

#その他計算条件
time=np.arange(0,11,1)  # 時間の条件入力

#方程式定義
def fA(A,t):
    return -k*A

#odeint定義
y=odeint(fA,A,time)  #括弧内(方程式,初期値,時間条件)

print(y)

変更点は主に、

2,3行目：scipy、numpyを使用するためインポートする。
12行目：時間の条件入力をする。括弧内は時間tの(計算開始値,計算終了値,刻み幅)。
19行目：odeintを入力する。

以上です。計算すると、


[[10.        ]
 [ 9.04837431]
 [ 8.18730761]
 [ 7.40818226]
 [ 6.70320054]
 [ 6.06530669]
 [ 5.48811646]
 [ 4.96585314]
 [ 4.49328986]
 [ 4.06569672]
 [ 3.67879456]]

とyの値(ここでは濃度A)が出力されます。

出力される桁数こそ違うものの、前述したRunge-Kutta法での結果とほとんど同じになりました。

コードの記述がかなり減って楽になるので、慣れてくればこのようなライブラリを積極的に使っていきたいところです。

まとめ

Pythonでタンク内の原料濃度変化をEuler法とRunge-Kutta法の両方で計算し、グラフで比較してみました。

Runge-Kutta法は計算コストの割に計算精度が良いので、実務ではよく使用されます。覚えておきましょう。