概要
本記事ではPythonでの化学工学計算例を紹介しています。今回は連立常微分方程式の例として、タンク内の濃度・温度変化を計算します。
プラントでの実現象として複数のパラメータが経時的に変化することはよくあることです。
何らかの仮定を置きパラメータを1つに絞って微分方程式を立てるテクニックも重要ですが、必ずそのテクニックを使えるわけではありません。
常微分方程式を連立して解くことに慣れておいた方が良いと思います。
計算の前提条件

上図に示すようなタンクに、ある時刻から液体をF=100kg/min、Ti=100℃で流入させます。タンク内にはもともとM0=1,000kg、T0=25 ℃の液体が入っているものとします。
このときの1h後のタンク内の液体の質量Mと温度Tの経時変化を計算します。
現象のモデル化
物質収支
まずは物質収支を取ります。セミバッチ式のタンクで流出する液体はありませんから、
$$\frac{dM}{dt}=F・・・(1)$$
(1)式のように表すことができます。
この(1)式だけならば手計算で簡単に解くことができますが、今回は温度変化も計算する必要があります。
そのため、(1)式は数値微分で解きます。
熱収支
次に熱収支を取ります。タンク内の液体の質量M、温度Tの両方が変化することを考慮すると、
$$\frac{Δ(M・T)}{Δt}C_{p}=FC_{p}T_{i} ・・・(2)$$
(2)式のように表すことができます。Cp[kcal/(kg・K)]は液比熱です。
(2)式を全微分すると、
$$(T\frac{ΔM}{Δt}+M\frac{ΔT}{Δt} )C_{p}=FC_{p}T_{i}$$
となりますが、後々Pythonに入力することを考えて、
$$\frac{ΔT}{Δt}=\frac{FT_{i}}{M}-\frac{T}{M}\frac{ΔM}{Δt} ・・・(3)$$
(3)式のように変形しておきます。
(3)式でΔ→0とすると、
$$\frac{dT}{dt}=\frac{FT_{i}}{M}-\frac{T}{M}\frac{dM}{dt} ・・・(4)$$
(4)式となります。これでPythonで解く式の導出は完了です。
数値微分
今回は(1),(4)式にEuler法を適用して解きましょう。導出は省きますがそれぞれ、
$$ M=M+Δt×\frac{dM}{dt}・・・(5) $$
$$ T=T+Δt×\frac{dT}{dt}・・・(6) $$
となります。
Python記述
ライブラリ・モジュールのインポート
今回は質量M、温度Tの2変数を計算しますが、経時変化のグラフを作ってみます。
Python上でグラフを作成するためのライブラリであるMatplotlibをインポートします。
#Matplotlibインポート
import matplotlib.pyplot as plt前提条件の入力
問題で与えられる前提条件を入力します。
#前提条件
F=100 # kg/min
Ti=100 # ℃初期条件の入力
次に初期条件が必要な場合はその値を入力します。
今回は時間t、質量M、温度Tの初期値を入力します。
#初期条件
t=0 # min
M=1000 # kg
T=25 # ℃その他計算条件の入力
今回は時間刻みΔtと繰り返し計算回数imaxを入力します。
#その他計算条件
dt=1 # min
imax=61時間刻みはΔt=1minとしました。
また、for文を使って繰り返し計算を行なう予定なので、繰り返し計算回数をimaxとして入力します。
imax=61としました。時間tを1min刻みで0.0~60minまで計算するので、繰り返し回数は61回となります。
グラフ作成用配列の入力
グラフ作成用の配列として、gt、gM、gTと名付けた空の配列を設定します。
この配列に計算値が入るように後で入力します。
#グラフ作成用
gt = []
gM = []
gT = []方程式の定義
次にメインの方程式(1),(4)式を定義します。
#方程式定義
def fM(M):
return F # (1)式
def fT(T,M):
return F/M*Ti-T/M*fM(M) # (4)式Euler法の入力
続いてEuler法を入力していきます。
今回はfor文を使用して繰り返し計算を入力します。
#Euler法
for i in range(imax):
print('i:{0:4d}, t:{1:6.2f}, M:{2:6.0f}, T:{3:6.1f}' .format(i,t,M,T))
gt.append(t)
gM.append(M)
gT.append(T)
M=M+dt*fM(M) # (5)式
T=T+dt*fT(T,M) # (6)式
t=t+dt # 時間の更新 2行目はfor文の文法にしたがって記入しています。繰り返し回数をiとおき、括弧内には繰り返し計算回数imaxを入力します。
3行目はprint関数でi,t,M,Tの繰り返し計算結果を出力しています。
5~7行目でappendを使用して指定した配列に計算値を加えるように入力しています。
5行目で配列gtに時間tを追加、6行目で配列gMに質量Mを追加、7行目で配列gTに温度Tを追加しています。
9行目で(5)式、10行目で(6)式のEuler法を入力しています。
11行目で時間tの更新をしています。
グラフの出力
最後にグラフの出力に関するコードを記入します。
今回は横軸の時間tに対して質量M、温度Tを2軸でプロットしてみます。
#グラフ出力
fig = plt.figure()
tM = fig.subplots()
tT = tM.twinx() # 2軸の追加
tM.plot(gt, gM,label='M') #gt,gMのプロット
tT.plot(gt, gT,label="T",color="r") #gt,gTのプロット
tM.set_xlabel("t [min]") #x軸ラベル
tM.set_ylabel("M [kg]") #第1y軸のラベル
tT.set_ylabel("T [℃]") #第2y軸のラベル
handler1, label1 = tM.get_legend_handles_labels() #tM.plotからラベルの取得
handler2, label2 = tT.get_legend_handles_labels() #tT.plotからラベルの取得
tM.legend(handler1 + handler2, label1 + label2) #凡例の表示
plt.show() 3行目で第1y軸として質量Mを入力しています。名前をtMと付けていますがわかれば何でも良いです。
4行目でグラフに第2y軸である温度Tを追加しています。
5行目で横軸gt、縦軸gMをプロットしています。また、凡例に表示させる文字としてMを入力しています。
6行目で横軸gt、縦軸gTをプロットし、凡例表示としてTを入力しています。
また、デフォルトでは2つのプロットが同じ色で表示されて見分けがつきにくいので片方の色を変えます。
color="r"と入力することで温度Tのプロットが赤色で表示されます。
7行目でx軸のラベル、8行目で第1y軸のラベル、9行目で第2y軸のラベルを入力します。
10行目で5行目のtM.plotから凡例ラベルの取得をしています。
11行目で6行目のtT.plotから 凡例ラベルの取得をしています。
12行目で凡例をまとめて表示しています。
計算結果の確認
特に入力ミス等がなければ計算結果が以下のように表示されます。
i: 0, t: 0.00, M: 1000, T: 25.0
i: 1, t: 1.00, M: 1100, T: 31.8
i: 2, t: 2.00, M: 1200, T: 37.5
i: 3, t: 3.00, M: 1300, T: 42.3
i: 4, t: 4.00, M: 1400, T: 46.4
i: 5, t: 5.00, M: 1500, T: 50.0
i: 6, t: 6.00, M: 1600, T: 53.1
i: 7, t: 7.00, M: 1700, T: 55.9
i: 8, t: 8.00, M: 1800, T: 58.3
i: 9, t: 9.00, M: 1900, T: 60.5
i: 10, t: 10.00, M: 2000, T: 62.5
i: 11, t: 11.00, M: 2100, T: 64.3
i: 12, t: 12.00, M: 2200, T: 65.9
i: 13, t: 13.00, M: 2300, T: 67.4
i: 14, t: 14.00, M: 2400, T: 68.8
i: 15, t: 15.00, M: 2500, T: 70.0
i: 16, t: 16.00, M: 2600, T: 71.2
i: 17, t: 17.00, M: 2700, T: 72.2
i: 18, t: 18.00, M: 2800, T: 73.2
i: 19, t: 19.00, M: 2900, T: 74.1
i: 20, t: 20.00, M: 3000, T: 75.0
i: 21, t: 21.00, M: 3100, T: 75.8
i: 22, t: 22.00, M: 3200, T: 76.6
i: 23, t: 23.00, M: 3300, T: 77.3
i: 24, t: 24.00, M: 3400, T: 77.9
i: 25, t: 25.00, M: 3500, T: 78.6
i: 26, t: 26.00, M: 3600, T: 79.2
i: 27, t: 27.00, M: 3700, T: 79.7
i: 28, t: 28.00, M: 3800, T: 80.3
i: 29, t: 29.00, M: 3900, T: 80.8
i: 30, t: 30.00, M: 4000, T: 81.2
i: 31, t: 31.00, M: 4100, T: 81.7
i: 32, t: 32.00, M: 4200, T: 82.1
i: 33, t: 33.00, M: 4300, T: 82.6
i: 34, t: 34.00, M: 4400, T: 83.0
i: 35, t: 35.00, M: 4500, T: 83.3
i: 36, t: 36.00, M: 4600, T: 83.7
i: 37, t: 37.00, M: 4700, T: 84.0
i: 38, t: 38.00, M: 4800, T: 84.4
i: 39, t: 39.00, M: 4900, T: 84.7
i: 40, t: 40.00, M: 5000, T: 85.0
i: 41, t: 41.00, M: 5100, T: 85.3
i: 42, t: 42.00, M: 5200, T: 85.6
i: 43, t: 43.00, M: 5300, T: 85.8
i: 44, t: 44.00, M: 5400, T: 86.1
i: 45, t: 45.00, M: 5500, T: 86.4
i: 46, t: 46.00, M: 5600, T: 86.6
i: 47, t: 47.00, M: 5700, T: 86.8
i: 48, t: 48.00, M: 5800, T: 87.1
i: 49, t: 49.00, M: 5900, T: 87.3
i: 50, t: 50.00, M: 6000, T: 87.5
i: 51, t: 51.00, M: 6100, T: 87.7
i: 52, t: 52.00, M: 6200, T: 87.9
i: 53, t: 53.00, M: 6300, T: 88.1
i: 54, t: 54.00, M: 6400, T: 88.3
i: 55, t: 55.00, M: 6500, T: 88.5
i: 56, t: 56.00, M: 6600, T: 88.6
i: 57, t: 57.00, M: 6700, T: 88.8
i: 58, t: 58.00, M: 6800, T: 89.0
i: 59, t: 59.00, M: 6900, T: 89.1
i: 60, t: 60.00, M: 7000, T: 89.3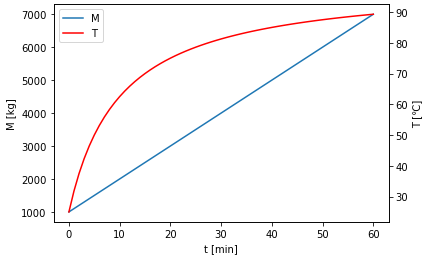
計算結果が数字とグラフの両方で表示されます。
グラフはちゃんと指定した通りのラベルと色になっていますね。
下に計算コードを最初から最後までまとめて載せておきます。
#Matplotlibインポート
import matplotlib.pyplot as plt
#前提条件
F=100 # kg/min
Ti=100 # ℃
#初期条件
t=0 # min
M=1000 # kg
T=25 # ℃
#その他計算条件
dt=1 # min
imax=61
#グラフ作成用
gt = []
gM = []
gT = []
#方程式定義
def fM(M):
return F # (1)式
def fT(T,M):
return F/M*Ti-T/M*fM(M) # (4)式
#Euler法
for i in range(imax):
print('i:{0:4d}, t:{1:6.2f}, M:{2:6.0f}, T:{3:6.1f}' .format(i,t,M,T))
gt.append(t)
gM.append(M)
gT.append(T)
M=M+dt*fM(M) # (5)式
T=T+dt*fT(T,M) # (6)式
t=t+dt # 時間の更新
#グラフ出力
fig = plt.figure()
tM = fig.subplots()
tT = tM.twinx() # 2軸の追加
tM.plot(gt, gM,label='M') #gt,gMのプロット
tT.plot(gt, gT,label="T",color="r") #gt,gTのプロット
tM.set_xlabel("t [min]") #x軸ラベル
tM.set_ylabel("M [kg]") #第1y軸のラベル
tT.set_ylabel("T [℃]") #第2y軸のラベル
handler1, label1 = tM.get_legend_handles_labels() #tM.plotからラベルの取得
handler2, label2 = tT.get_legend_handles_labels() #tT.plotからラベルの取得
tM.legend(handler1 + handler2, label1 + label2) #凡例の表示
plt.show() まとめ
Pythonでタンク内の濃度・温度変化に関する連立常微分方程式を計算する方法を解説しました。
それぞれの微分方程式にEuler法等の数値微分を適用することで解くことができます。
