※当ブログではアフィリエイト・Google Adsense・The Moneytizerによる広告を掲載しています。

数値解析 Python

【Python】Gauss-Newton法の解説：Antoine式の定数決定

2021年11月13日

概要

Gauss-Newton法は非線形最小二乗法の解法の1つです。

Newton法で計算が重いとされるヘッセ行列をヤコビ行列で近似することで計算を軽くしていることが特徴です。

うまく初期値を選ぶ必要はありますが多少複雑な非線形関数でも収束するため、化学工学の分野では実用に近い解法と言えるでしょう。

原理

m個のデータと最もよくフィッティングするように非線形最小二乗法を使用することを考えます。

フィッティングさせる関数はy=f(x,β)で表されるものとし、最小二乗法でパラメータβ=(β1,β2,・・・βn)を決定します。

線形最小二乗法の記事で述べたのと同様に、任意のデータ点(xi,yi)と近似関数y=f(x,β)との残差riは、

$$r_{i}(β)=y_{i}-f(x,β)・・・(1)$$

(1)式で表されます。

(1)式の平方和を取ると、

$$S(β)=\sum_{i=1}^{m}r_{i}(β)・・・(2)$$

(2)式となります。この(2)式の目的関数S(β)を最小化するようにパラメータβを決定します。

S(β)を微小刻みaの周りでTaylor展開し、2次の項までで近似すると、

$$\begin{align}S(β+a)&=S(β)+∇S(β)a+\frac{∇^{2}S(β)a^{2}}{2!}+・・・\\&
≒S(β)+∇S(β)a+\frac{∇^{2}S(β)a^{2}}{2}・・・(3)\end{align}$$

(3)式となります。

(3)式をaについて微分してゼロになれば極小値を持ちますので、

$$\frac{d(S(β+a))}{da}=∇S(β)+∇^{2}S(β)a=0$$

$$a=-(∇^{2}S(β))^{-1}∇S(β)・・・(4)$$

(4)式となります。(4)式からaを求め、

$$β_{n+1}=β_{n}+a・・・(5)$$

(5)式に代入することで繰り返し計算が可能です。ここまでが通常のNewton法の解法となります。

(4)式にはヘッセ行列H=∇2S(β)が含まれており、変数の数が多くなってくると非常に計算負荷が高くなるのが特徴です。

そこでこのヘッセ行列を相対的に計算負荷の少ないヤコビ行列に近似したのがGauss-Newton法になります。

ヘッセ行列を近似するステップとして、まずはS(β)の勾配gを計算しましょう。

$$g_{j}=∇S_{n}(β)=2\sum_{i=1}^{m}r_{i}\frac{∂r_{i}}{∂β_{j}}・・・(6)$$

(6)式をヤコビ行列Jの転置行列JTで表すと、

$$\boldsymbol{g}=2\boldsymbol{J}^{T}\boldsymbol{r}・・・(7)$$

(7)式となります。

次に(6)式を再びβで微分するとヘッセ行列Hとなります。

$$H_{jk}=∇^{2}S_{n}(β)=2\sum_{i=1}^{m}r_{i}(\frac{∂r_{i}}{∂β_{j}}\frac{∂r_{i}}{∂β_{k}}+r_{i}\frac{∂^{2}r_{i}}{∂β_{j}∂β_{k}})・・・(8)$$

ここで(8)式の2項目について、十分に解の近くであることを想定するとゼロに近似できます。したがって、

$$H_{jk}=∇^{2}S_{n}(β)=2\sum_{i=1}^{m}r_{i}(\frac{∂r_{i}}{∂β_{j}}\frac{∂r_{i}}{∂β_{k}})・・・(9)$$

(9)式となります。(9)式をヤコビ行列で表すと、

$$\boldsymbol{H}=2\boldsymbol{J}^{T}\boldsymbol{J}・・・(10)$$

(10)式となります。

(7)、(10)式で(5)式を表わすと、

$$β_{n+1}=β_{n}-( \boldsymbol{J}^{T}\boldsymbol{J} )^{-1} \boldsymbol{J}^{T}\boldsymbol{r} ・・・(11)$$

(11)式となり、ヘッセ行列の代わりにヤコビ行列で表すことができました。

また、データの個数mとパラメータβの数nが等しい場合(m=n)、(11)式は

$$β_{n+1}=β_{n}-( \boldsymbol{J} )^{-1} \boldsymbol{r} ・・・(12)$$

(12)式に簡略化することができます。

Pythonでの計算法

計算条件

Antoine式のパラメータA、B、Cを温度・圧力データから決定しましょう。

有名な化合物であれば商用シミュレーターにすでにAntoineパラメータが登録されていると思いますが、社内で新規に開発された化合物やマイナーな化合物は自分たちで温度・圧力データを取ってフィッティングすることになるでしょう。

今回はその練習です。

温度T[℃]圧力P[kPa]
64.51101.325
66.14107.9911184
67.83115.283852
69.58123.2431974
71.29131.4691875
73.16140.9750724
75.36152.8807599
77.90167.6395461
81.48190.4243388
84.01208.0095592
87.53234.6607007
92.39276.0039671
100.00352.4910099

今回は上の表のデータを使用してAntoineパラメータを決定します。

もし実験データを取るときは、設計する予定のプラントの運転温度・圧力に近いところで取り、運転データが実験データの内挿となることが望ましいです。

残差の作成

Antoine式は、

$${\rm{log}}_{10}P=A-\frac{B}{T+C}・・・(13)$$

P：圧力[kPa]、T：温度[℃]

(13)式で表されます。ちなみに、参考書によって温度・圧力の単位や常用対数、自然対数のどちらを使用するかが変わってくるのでよく確認しましょう。

(1)式の残差rは(13)式をP=の形に変形して、

$$r=P_{th}-P_{cal}=P_{th}-10^{(A-\frac{B}{T+C})}・・・(14)$$

(14)式となります。

これでPythonで計算する準備が整いました。

ライブラリ・モジュールのインポート

ここからPythonでの記述となります。

NumpyとMatplotlibをインポートします。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt

前提条件

問題で与えられた前提条件を入力します。

#前提条件の入力
T=np.array([64.51,66.14,67.83,69.58,71.29,73.16,75.36,77.9,81.48,84.01,87.53,92.39,100.])
P=np.array([101.325,107.9911184,115.283852,123.2431974,131.4691875,140.9750724,152.8807599,167.6395461,190.4243388,208.0095592,234.6607007,276.0039671,352.4910099])

Antoine式の入力

Antoine式をdef文で入力します。

#Antoine式
def theoreticalValue(beta):
    Pcal=10**(beta[0]+beta[1]/(T+beta[2]))
    return Pcal

残差の入力

(14)式の残差をdef文で入力します。

#残差
def objectiveFunction(beta):
    r = P - theoreticalValue(beta)
    return r

Gauss-Newton法の入力

メインのGauss-Newton法を入力します。

#Gauss-Newton法
def gaussNewton(function, beta, tolerance, epsilon):    
    delta = 2*tolerance
    alpha = 1
    while np.linalg.norm(delta) > tolerance:
        F = function(beta)
        J = np.zeros((len(F), len(beta)))  # 有限差分ヤコビアン
        for jj in range(0, len(beta)):
            dBeta = np.zeros(beta.shape)
            dBeta[jj] = epsilon
            J[:, jj] = (function(beta+dBeta)-F)/epsilon
        delta = -np.linalg.pinv(J).dot(F)  # 探索方向
        beta = beta + alpha*delta
    return beta

Gauss-Newton法の実行

定義したGauss-Newton法の実行を記述しています。

#Gauss-Newton法の実行
initialValue = np.array([1,1,1])
#initialValue = np.array([10,-100,100])
#initialValue = np.array([10,-1500,200])
betaID = gaussNewton(objectiveFunction, initialValue, 1e-4, 1e-4)

今回は初期値依存性を見るために、何ケースか初期値を変えてみました。

(A0,B0,C0)=(1,1,1),(10,-100,100),(10,-1500,200)の3ケースです。

グラフ作成

フィッティング度合いを確認するためにグラフを作成します。

#グラフの出力
print(betaID)
plt.figure()
plt.plot(T, P,'o')
plt.plot(T, theoreticalValue(betaID),'-')
plt.xlabel('T [℃]')
plt.ylabel('P [kPa]')
plt.legend(['Row data','Pcal'])
plt.show()

計算結果の確認

まずは初期値 (A0,B0,C0)=(1,1,1)のケースの計算結果を見てみましょう。


[-2.11955839e+01 -2.44583621e+06  9.72680305e+04]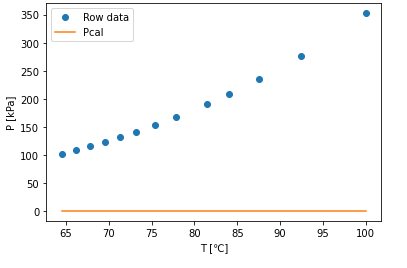

全くあっていません。やはりいい加減な初期値ではうまくいかないようです。

次に初期値 (A0,B0,C0)=(10,-100,100)のケースの計算結果を見てみましょう。


[ 1.43213551e+02 -1.34007797e+07  6.04693726e+04]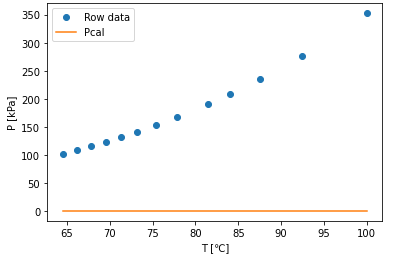

ある程度収束解に近い初期値にしましたが、これでもうまくいきません。

最後に初期値 (A0,B0,C0)=(10,-1500,200)のケースの計算結果を見てみましょう。


[ 7.13144455 -1540.27893673  235.99031195]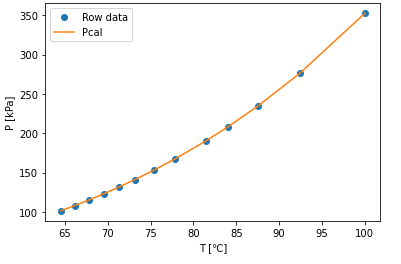

こんどはきちんと元データに合う曲線が引けました。結果として、(A,B,C)=( 7.13, -1540.28, 235.99)となりました。

Antoine式はそれぞれのパラメータの桁くらいは予想できるので、うまくフィッティング出来ない場合は初期値を色々と試してみましょう。

全体のコードを下に載せておきます。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt

#前提条件の入力
T=np.array([64.51,66.14,67.83,69.58,71.29,73.16,75.36,77.9,81.48,84.01,87.53,92.39,100.])
P=np.array([101.325,107.9911184,115.283852,123.2431974,131.4691875,140.9750724,152.8807599,167.6395461,190.4243388,208.0095592,234.6607007,276.0039671,352.4910099])

#Antoine式
def theoreticalValue(beta):
    Pcal=10**(beta[0]+beta[1]/(T+beta[2]))
    return Pcal

#残差
def objectiveFunction(beta):
    r = P - theoreticalValue(beta)
    return r

#Gauss-Newton法
def gaussNewton(function, beta, tolerance, epsilon):    
    delta = 2*tolerance
    alpha = 1
    while np.linalg.norm(delta) > tolerance:
        F = function(beta)
        J = np.zeros((len(F), len(beta)))  # 有限差分ヤコビアン
        for jj in range(0, len(beta)):
            dBeta = np.zeros(beta.shape)
            dBeta[jj] = epsilon
            J[:, jj] = (function(beta+dBeta)-F)/epsilon
        delta = -np.linalg.pinv(J).dot(F)  # 探索方向
        beta = beta + alpha*delta
    return beta

#Gauss-Newton法の実行
#initialValue = np.array([1,1,1])
#initialValue = np.array([10,-100,100])
initialValue = np.array([10,-1500,200])
betaID = gaussNewton(objectiveFunction, initialValue, 1e-4, 1e-4)

#グラフの出力
print(betaID)
plt.figure()
plt.plot(T, P,'o')
plt.plot(T, theoreticalValue(betaID),'-')
plt.xlabel('T [℃]')
plt.ylabel('P [kPa]')
plt.legend(['Row data','Pcal'])
plt.show()

まとめ

Antoine式のパラメータフィッティングを例にPythonでGauss-Newton法の解説をしました。

非線形方程式の収束計算では初期値は常に重要になります。理論的にある程度初期値を予測できる場合もありますので色々試してみましょう。