【Python】Levenberg-Marquardt法を解説：Antoine式の定数決定

概要

Levenberg-Marquardt法は非線形最小二乗法の解法の1つです。

最急降下法とGauss-Newton法の良いところを組み合わせることで収束性が向上しています。

Pythonで計算する場合はScipyのleasteq関数を使用すれば簡単にMarquardt法で計算することができます。

原理

式の導出は途中までGauss-Newton法と全く同じです。

Gauss-Newton法ではフィッティングするパラメータβの更新式は(1)式で表されます。

$$β_{n+1}=β_{n}-( \boldsymbol{J}^{T}\boldsymbol{J} )^{-1} \boldsymbol{J}^{T}\boldsymbol{r} ・・・(1)$$

(1)式をパラメータλと単位行列Iで修正し、

$$β_{n+1}=β_{n}-( \boldsymbol{J}^{T}\boldsymbol{J}+λ\boldsymbol{I} )^{-1} \boldsymbol{J}^{T}\boldsymbol{r} ・・・(2)$$

(2)式としたものがLevenberg-Marquart法の式となります。

仮に(2)式でλの値が大きい場合はヤコビ行列の積J^TJの値が小さく無視できるため、

$$β_{n+1}=β_{n}-λ\boldsymbol{I}^{-1} \boldsymbol{J}^{T}\boldsymbol{r}=λ \boldsymbol{I}^{-1}\boldsymbol{g}・・・(3)$$

(3)式となります。(3)式の形は最急降下法と同じようにパラメータλと勾配gで表されるため、最急降下法と同様の計算結果が得られます。

一方でλの値が小さい場合はλIの項が小さく無視できるため、

$$β_{n+1}=β_{n}-( \boldsymbol{J}^{T}\boldsymbol{J})^{-1} \boldsymbol{J}^{T}\boldsymbol{r} ・・・(4)$$

(4)式となり、(1)式と一致するためGauss-Newton法と同じ計算結果が得られます。

したがって、収束解から遠いときはλを大きい値として最急降下法の成分を強くして計算することで収束解に近づけることができます。

計算結果が収束解に近くなると、λを小さくすることでGauss-Newton法の成分を強くして一気に収束させることができます。

このようにGauss-Newton法の欠点である初期値依存性をある程度補えること、あるいは最急降下法の欠点である計算回数がかかり過ぎる点をそれぞれ補えることがこのLevenberg-Marquart法のメリットです。

Pythonでの計算法

Gauss-Newtonの記事で紹介したAntoine式のパラメータフィッティングをLevenberg-Marquart法でもやってみましょう。

初期値を変えてみてどのくらい収束しやすくなっているか確認しました。

計算条件

温度、圧力条件は以下に示す通りです。

温度T[℃]	圧力P[kPa]
64.51	101.325
66.14	107.9911184
67.83	115.283852
69.58	123.2431974
71.29	131.4691875
73.16	140.9750724
75.36	152.8807599
77.90	167.6395461
81.48	190.4243388
84.01	208.0095592
87.53	234.6607007
92.39	276.0039671
100.00	352.4910099

残差の作成

Antoine式は、

$${\rm{log}}_{10}P=A-\frac{B}{T+C}・・・(13)$$

P：圧力[kPa]、T：温度[℃]

(13)式で表されます。ちなみに、参考書によって温度・圧力の単位や常用対数、自然対数のどちらを使用するかが変わってくるのでよく確認しましょう。

(1)式の残差rは(13)式をP=の形に変形して、

$$r=P_{th}-P_{cal}=P_{th}-10^{(A-\frac{B}{T+C})}・・・(14)$$

(14)式となります。

これでPythonで計算する準備が整いました。

ライブラリ・モジュールのインポート

ここからPythonでの記述となります。

今回はLevenberg-Marquart法を簡単に使えるScipyのleastsq関数をインポートします。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

前提条件

問題で与えられた前提条件を入力します。

#前提条件の入力
T=np.array([64.51,66.14,67.83,69.58,71.29,73.16,75.36,77.9,81.48,84.01,87.53,92.39,100.])
P=np.array([101.325,107.9911184,115.283852,123.2431974,131.4691875,140.9750724,152.8807599,167.6395461,190.4243388,208.0095592,234.6607007,276.0039671,352.4910099])

Antoine式の入力

Antoine式をdef文で入力します。

#Antoine式
def theoreticalValue(beta):
    Pcal=10**(beta[0]+beta[1]/(T+beta[2]))
    return Pcal

残差の入力

(14)式の残差をdef文で入力します。

#残差
def objectiveFunction(beta):
    r = P - theoreticalValue(beta)
    return r

Levenberg-Marquardt法の実行

定義したLevenberg-Marquardt法の実行を記述しています。

#Levenberg-Marquardt法の実行
initialValue = np.array([1,1,1])
#initialValue = np.array([10,-100,100])
#initialValue = np.array([10,-1500,200])
betaL = leastsq(objectiveFunction,initialValue,maxfev=1000)

今回は初期値依存性を見るために、何ケースか初期値を変えてみました。

(A₀,B₀,C₀)=(1,1,1),(10,-100,100),(10,-1500,200)の3ケースです。

Gauss-Newton法との比較

Gauss-Newton法と計算結果を比較するために、こちらの記事で紹介したコードを入力しています。

#Gauss-Newton法
def gaussNewton(function, beta, tolerance, epsilon):    
    delta = 2*tolerance
    alpha = 1
    while np.linalg.norm(delta) > tolerance:
        F = function(beta)
        J = np.zeros((len(F), len(beta)))  # 有限差分ヤコビアン
        for jj in range(0, len(beta)):
            dBeta = np.zeros(beta.shape)
            dBeta[jj] = epsilon
            J[:, jj] = (function(beta+dBeta)-F)/epsilon
        delta = -np.linalg.pinv(J).dot(F)  # 探索方向
        beta = beta + alpha*delta
    return beta

betaG = gaussNewton(objectiveFunction, initialValue, 1e-4, 1e-4)

グラフ作成

フィッティング度合いを確認するためにグラフを作成します。

#グラフの出力
print('Gauss-Newton{0}'.format(betaG))
print('Levenberg-Marquardt{0}'.format(betaL))
plt.figure()
plt.plot(T, P,'o')
plt.plot(T, theoreticalValue(betaG),'-')
plt.plot(T, theoreticalValue(betaL[0]),'-')
plt.xlabel('T [℃]')
plt.ylabel('P [kPa]')
plt.legend(['Row data','Gauss-Newton','Levenberg-Marquardt'])
plt.show()

計算結果の確認

まずは初期値 (A₀,B₀,C₀)=(1,1,1)のケースの計算結果を見てみましょう。


C:\python\lib\site-packages\scipy\optimize\minpack.py:475: RuntimeWarning: Number of calls to function has reached maxfev = 1000.
  warnings.warn(errors[info][0], RuntimeWarning)
Gauss-Newton[-2.11955839e+01 -2.44583621e+06  9.72680305e+04]
Levenberg-Marquardt(array([   -9.00704994, -8561.77770423,  -840.58672347]), 5)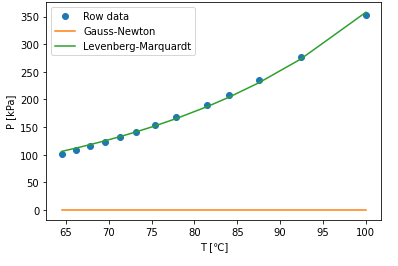

出力画面にはエラー表示が出たものの、print関数の結果とグラフも表示されました。

エラー文はleasteq関数で指定している計算回数1000回に達しても収束しなかったために表示されています。

計算結果を見てみると、Gauss-Newton法は全くフィッティングできていないのに対して、Levenberg-Marquardt法はある程度フィッティングできていますね。しかしAntoineパラメータA,B,Cが微妙にずれているためフィッティングも少しずれています。

次に初期値 (A₀,B₀,C₀)=(10,-100,100)のケースの計算結果を見てみましょう。


Gauss-Newton[ 1.43213551e+02 -1.34007797e+07  6.04693726e+04]
Levenberg-Marquardt(array([    7.13144452, -1540.27892161,   235.99031038]), 3)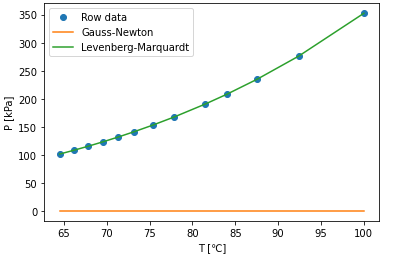

Gauss-Newton法はまだ全然フィッティングしていませんが、Levenberg-Marquardt法は完全にフィッティングすることができました。

最後に初期値 (A₀,B₀,C₀)=(10,-1500,200)のケースの計算結果を見てみましょう。


Gauss-Newton[    7.13144455 -1540.27893673   235.99031195]
Levenberg-Marquardt(array([    7.13144455, -1540.27894025,   235.99031232]), 2)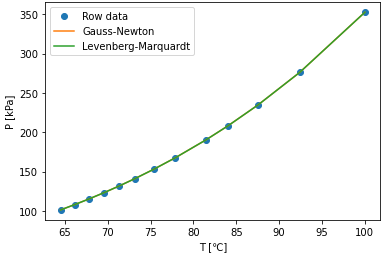

Gauss-Newton法、Levenberg-Marquardt法の両方とも完全にフィッティングしました。

以上、3ケースの初期値を試してみましたが、Levenberg-Marquardt法は初期値が収束解から遠くても収束しやすいことがわかりました。実用的にはLevenberg-Marquardt法を使用するのがよいでしょう。

全体のコードを下に載せておきます。

#モジュールインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq

#前提条件の入力
T=np.array([64.51,66.14,67.83,69.58,71.29,73.16,75.36,77.9,81.48,84.01,87.53,92.39,100.])
P=np.array([101.325,107.9911184,115.283852,123.2431974,131.4691875,140.9750724,152.8807599,167.6395461,190.4243388,208.0095592,234.6607007,276.0039671,352.4910099])

#Antoine式
def theoreticalValue(beta):
    Pcal=10**(beta[0]+beta[1]/(T+beta[2]))
    return Pcal

#残差
def objectiveFunction(beta):
    r=P-theoreticalValue(beta)
    return r

#Levenberg-Marquardt法の実行
#initialValue = np.array([1,1,1])
#initialValue = np.array([10,-100,100])
initialValue = np.array([10,-1500,200])
betaL = leastsq(objectiveFunction,initialValue,maxfev=1000)

#Gauss-Newton法
def gaussNewton(function, beta, tolerance, epsilon):    
    delta = 2*tolerance
    alpha = 1
    while np.linalg.norm(delta) > tolerance:
        F = function(beta)
        J = np.zeros((len(F), len(beta)))  # 有限差分ヤコビアン
        for jj in range(0, len(beta)):
            dBeta = np.zeros(beta.shape)
            dBeta[jj] = epsilon
            J[:, jj] = (function(beta+dBeta)-F)/epsilon
        delta = -np.linalg.pinv(J).dot(F)  # 探索方向
        beta = beta + alpha*delta
    return beta

betaG = gaussNewton(objectiveFunction, initialValue, 1e-4, 1e-4)


#グラフの出力
print('Gauss-Newton{0}'.format(betaG))
print('Levenberg-Marquardt{0}'.format(betaL))
plt.figure()
plt.plot(T, P,'o')
plt.plot(T, theoreticalValue(betaG),'-')
plt.plot(T, theoreticalValue(betaL[0]),'-')
plt.xlabel('T [℃]')
plt.ylabel('P [kPa]')
plt.legend(['Row data','Gauss-Newton','Levenberg-Marquardt'])
plt.show()

まとめ

Antoine式のパラメータフィッティングを例にPythonでLevenberg-Marquardt法の解説をしました。

最急降下法とGauss-Newton法の良いとこどりをしたような手法で、使いやすいです。特に初期値が適当でも収束しやすいのは非常に助かります。