概要
Euler法(オイラー法)は常微分方程式を解く手法の1つです。十分に小さい刻み幅で差分を取ることにより、近似的に解を得ることができます。
簡単に微分できる式の場合は自分で微分して解いた方が早いかもしれませんが、微分することが難しい式の場合はEuler法のような数値微分の手法が非常に有効です。
また、化学工学では装置内の流体の濃度変化や温度変化を扱うことが多く、これらの現象を数式で表すと微分方程式になります。
そのためEuler法を使用して計算する機会も多いと思います。
本記事ではEuler法の計算手法について解説し、実際にタンク内の濃度変化に関する例題を解いてみます。
Euler法の計算手法
原理
$$\frac{dx}{dt}=f(x,t)・・・(1)$$
(1)式を積分することを考えます。
x=xn~xn+1、t=tn~tn+1の積分区間で(1)式を積分すると、
$$x_{n+1}-x_{n}=\int_{t_{n}}^{t_{n+1}}f(x,t)dt・・・(2)$$
(2)式となります。
したがって、右辺の関数f(x,t)をt=tn~tn+1の積分区間で積分できれば(1)式が解けることになります。
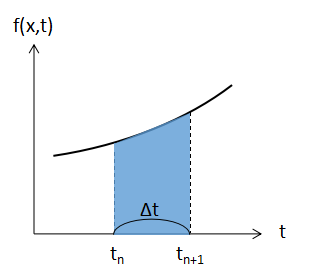
図で表すと(2)式の右辺は上の青い面積を表わします。
Euler法はこの青色の面積を下図で示すようなΔt・f(xn,tn)という緑色の長方形で近似的に表す手法です。
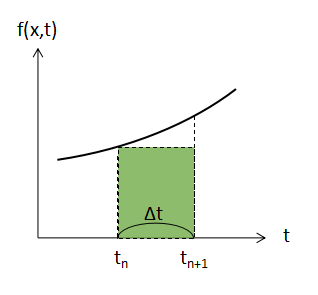
長方形は簡単に面積を求められる利点がある一方で、元の青色の面積と比較して誤差が大きくなりやすいのが欠点です。
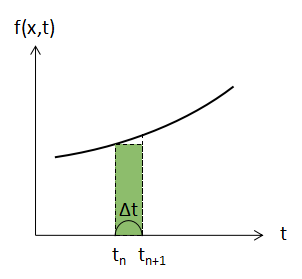
この欠点の対策として、上図のように刻み幅Δtを小さく取ることで誤差を少なくすることができます。
計算式
関数f(x)を初期値x0の近傍x0+ΔxでTaylor展開します。
$$f(x_{0}+Δx)=f(x_{0})+\frac{Δx}{1!}f'(x_{0})+\frac{Δx^{2}}{2!}f''(x_{0})+・・・ ・・・(3)$$
(3)式の2次以上の項は微小であり無視できますので、
$$f(x_{0}+Δx)=f(x_{0})+\frac{Δx}{1!}f'(x_{0})$$
したがって、f'(x)は
$$f'(x_{0})=\frac{f(x_{0}+Δx)-f(x_{0})}{Δx}・・・(4)$$
(4)式のように差分の形で表すことができます。
一般化すると、
$$f'(x_{n})=\frac{f(x_{n}+Δx)-f(x_{n})}{Δx}・・・(5)$$
(5)式のようになります。
また、このような数値解法は指定した区間で繰り返し計算を行なう手法であるため、(5)式を変形し
$$f( x_{n}+Δx )=f(x_{n+1})=f(x_{n})+Δxf'(x_{n})・・・(6)$$
(6)式の形で計算させることが多いです。
(6)式のように、xnにおける値や微分値からxn+1の値を求める手法を前進Euler法(もしくは単にEuler法)と呼びます。
前進Euler法があれば後進Euler法もあるわけですが、一般的な化学工学の分野では後進Euler法はそこまで使用頻度が高くないので割愛します。
ちなみに後進Euler法は収束安定性に優れるため、流動解析の分野ではよく使用されます。
例題:タンク内の濃度変化
計算条件
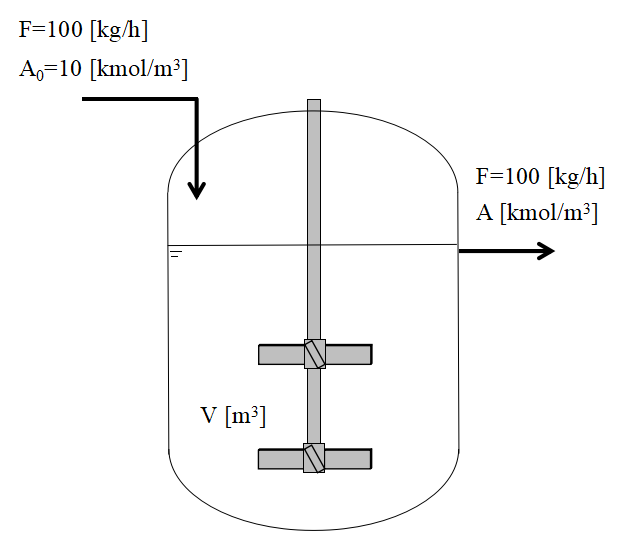
例題では上図に示すようなタンク内の原料濃度Aの変化を計算してみます。
タンクには初濃度A0=1.0kmol/m3の液体が入っており、ある時刻から濃度10.0kmol/m3の液体を流量100kg/hで連続的に流入させ、同時に同じ流量を抜き出します。
タンク内は十分に撹拌されており、完全混合状態だと仮定します。
このとき、5.0h後のタンク内の原料濃度Aを計算します。
なお、その他の条件として、
- 液体密度:1,000kg/m3
- タンク内の液体積:1.0m3
以上の条件がわかっているものとします。
基礎式の導出
まずはタンクに流入流出する原料について物質収支をとります。タンク内の原料濃度をAとすると、
$$V\frac{dA}{dt}=\frac{F}{ρ}(A_{0}-A)・・・(7)$$
(7)式のような物質収支が取れます。
Euler法を適用するために
$$\frac{dA}{dt}=\frac{F}{ρV}(A_{0}-A)・・・(8)$$
(8)式に式変形しておきます。
Euler法の適用
今回はとりあえずExcelで計算してみます。
まず時間刻みΔtを決定します。刻みが細かいほど精度が上がりますが、計算回数が増えます。
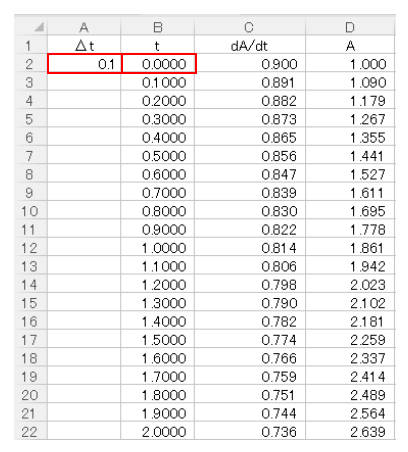
今回はΔt=0.1hとして設定しA2セルに入力します。
B2セルには時間の初期値としてt=0を入力し、B3セルはB2セル+$A$2セルと入力して時間変化を表わします。
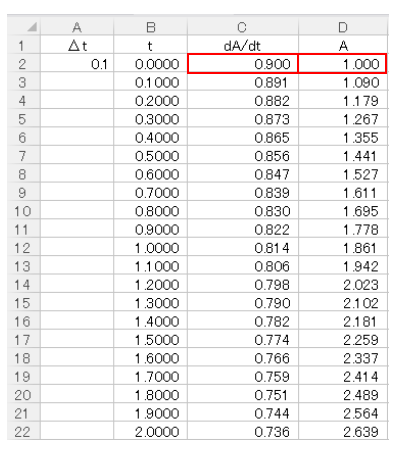
続いてC2セルに(8)式の右辺を入力します。原料濃度AはDの列に入力していき、D2セルにはAの初濃度1.0kmol/m3を入力します。
次に原料濃度AをEuler法で表しセルに記入していきます。
(6)式から、原料濃度Aは
$$A_{n+1}=A_{n}+Δt\frac{dA}{dt}・・・(9)$$
(9)式で表されます。
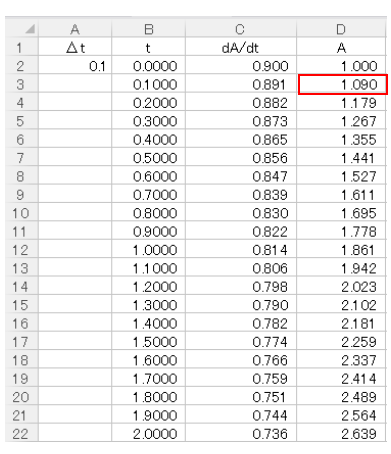
したがって、D3セルには
$$D3セル=D2セル+A2セル*C2セル$$
と入力します。
あとは同様の計算をt=5.0hとなるまで繰り返すだけです。Excelはセルをコピーすれば同様の計算を行ないやすいのが良い点ですね。
t=5.0hのときの計算結果を確認するとA=4.55mol/m3となりました。
参考までに、時間t=0.0~5.0hまでの原料濃度の推移を下のグラフに示しました。
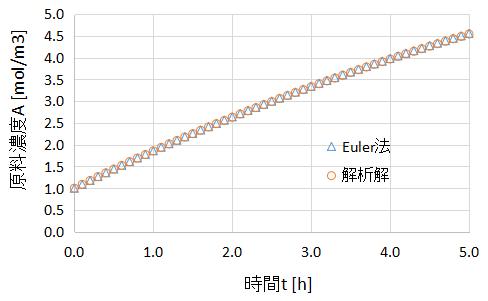
実は(5)式は積分することで解析解を算出することができます。
上のグラフでEuler法と解析解を比較してみましたが、今回の計算ではなかなか良い精度で一致しました。
前述しましたがEuler法の計算精度は刻み幅に依存するため、精度が悪い場合は刻み幅を小さくとることが精度向上の1つの策です。
まとめ
常微分方程式の解法の1つであるEuler法について解説しました。
微分することが難しい式の場合にはEuler法のような数値微分の手法が有効です。
実験して経時変化のデータを取ると微分方程式のような相関関係になりがちなので、大学時代にはEuler法だと知らずに似たような計算をしていた方もいらっしゃるのではないでしょうか。
私もとりあえず簡便に計算したい場合にはEuler法をよく使用します。
