ギブス自由エネルギーの定義
熱力学の第一法則・第二法則から、物質が持つ内部エネルギーと熱及び仕事はどれも変換可能なエネルギーであり、かつエネルギー変化の方向性が決まっていることがわかりました。
ただしこれらの法則では、物質とエネルギーの出入りのない孤立系であることを前提としています。
一方で、実際のプロセスでは系に外部からエネルギーを加える、あるいは外部へとエネルギーを放出する操作を行なうことがほとんどです。
そのため、外部からのエネルギーの出入りが可能な閉鎖系へと理論を拡張する必要があります。
このときに役に立つのが自由エネルギーの概念です。
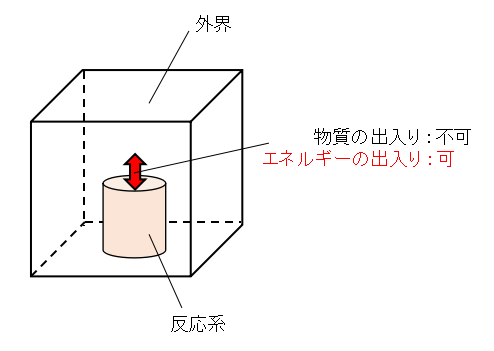
例えば上図に示すような系で不可逆な化学反応が起こることを考えましょう。
反応系は外界に囲まれており、温度一定となるように保たれるものとします。
加えて反応系と外界は物質の出入りは不可能ですがエネルギーの出入りが可能な閉鎖系とします。
また、反応系と外界を含めた全体は孤立系とします。
まず、反応系内で化学反応が起こると反応熱が発生し、反応系の温度を一定に保つために、反応熱は外界に吸収されます。
このときの反応熱と外界が吸収する熱量は絶対値が等しくなり、符号が反対となります。
$$Q_{sur}=-Q_{sys}・・・(1)$$
Qsur:外界が吸収する熱量、Qsys:反応熱
式で書くと(1)式となります。
次に、反応系と外界を含めた全体に対して、反応熱のやり取りによるエントロピー変化を考えると、
$$ΔS_{all}=ΔS_{sys}+ΔS_{sur}>0・・・(2)$$
ΔSall:全体のエントロピー変化
ΔSsys:反応系のエントロピー変化
ΔSsur:外界のエントロピー変化
(2)式となります。
(2)式から言えることは、全体のエントロピー変化ΔSallは必ずゼロ以上となる、ということだけです。
反応系や外界のエントロピー変化ΔSsys、ΔSsurがどうなるかは全くわからない一方で、ΔSallを知るためにはΔSsys、ΔSsurの値をそれぞれ知る必要があります。
実際に実験してデータを取ることを考えると、反応系は注目している系なので、データからΔSsysの値を求めることはできそうです。
しかし、外界の変化は実験環境に大きく依存し、容易にデータを取得できないことも多いでしょう。
そこで、全体のエントロピー変化ΔSallを反応系で取得できるデータやパラメータだけで表すことができれば非常に有用です。
この化学反応が温度一定下で起こっているとすると、エントロピーの定義式と(1)式から、
$$ΔS_{sur}=\frac{Q_{sur}}{T}=-\frac{Q_{sys}}{T}・・・(3)$$
ΔSsurは(3)式で表すことができます。
ここで、この化学反応が定圧過程だとすると、Qsys=ΔHsysとなるので、
$$ΔS_{sur}=-\frac{ΔH_{sys}}{T}・・・(4)$$
(4)式となります。
(4)式を(2)式に代入すると、
$$\begin{align}ΔS_{all}&=ΔS_{sys}-\frac{ΔH_{sys}}{T}\\&=-\frac{1}{T}(ΔH_{sys}-TΔS_{sys})>0・・・(5)\end{align}$$
(5)式となります。この(5)式により、全体のエントロピー変化ΔSallを反応系のパラメータΔHsys、ΔSsysなどから算出できるようになりました。
加えて、ΔSall>0となることから、右辺の括弧内は、
$$ΔH_{sys}-TΔS_{sur}<0・・・(6)$$
(6)式のように負の値となります。
ここで新たな状態量として、ギブス自由エネルギーGを(7)式のように定義します。
$$G=H-TS・・・(7)$$
すると(6)式は、
$$ΔG_{sys}=ΔH_{sys}-TΔS_{sur}<0・・・(8)$$
(8)式となります。
(5)式と(8)式から、全体のエントロピー変化ΔSall>0となり自発変化するときは、閉鎖系のギブス自由エネルギーΔGsys<0となることがわかります。
エントロピーSだけでは孤立系の自発変化しかわかりませんでしたが、ギブス自由エネルギーGにより閉鎖系の自発変化の方向がわかるようになりました。
このような孤立系から閉鎖系への理論の拡張が、ギブス自由エネルギーGを導入する意味合いの1つです。
ただし、(8)式までの導出でわかる通り、ギブス自由エネルギーGは等温定圧の閉鎖系を前提としています。
また、化学反応が完全に進行すると、エントロピーSは極大値を示しますが、逆にギブス自由エネルギーGは極小値を示します。
このとき、エントロピーS、ギブス自由エネルギーGはそれ以上値が変化しないため、各々の変化量ΔSall=0、ΔGsys=0となります。
したがって、閉鎖系が平衡状態に達したときはΔGsys=0となります。逆に言えば、相平衡や化学平衡に達している閉鎖系を考えるときは、ΔGsys=0となるように計算すればよいです。
混合のギブス自由エネルギー変化
エントロピーの記事では理想気体の混合エントロピーについて紹介しました。
$$ΔS=-n_{A}R{\rm{ln}}x_{A}-n_{B}R{\rm{ln}}x_{B}・・・(9)$$
混合エントロピー変化は(9)式となり、ΔS>0となります。
本記事では、同様に理想気体の混合におけるギブス自由エネルギー変化を考えてみます。
ギブス自由エネルギーの定義から、
$$ΔG=ΔH-TΔS・・・(10)$$
(10)式が成り立ちます。
理想気体の混合では温度変化がないため、ΔT=0、ΔU=0となります。
加えて、理想気体の状態方程式PV=nRTから、エンタルピー変化ΔHは、
$$ΔH=ΔU+Δ(PV)=ΔU+nRΔT=0・・・(11)$$
(11)式からゼロになります。
したがって、(10)、(11)式は、
$$ΔG=-TΔS=RT(n_{A}{\rm{ln}}x_{A}+n_{B}{\rm{ln}}x_{B})・・・(12)$$
(12)式となります。
モル分率xA、xBは0~1の値を示すため、(12)式はΔG<0となり、理想気体の混合は自発変化であることがわかります。
逆に、物質を分離する操作は混合とは真逆なので自発的に進まないということになります。
したがって、分離操作を行なう場合は、外部とエネルギーのやり取りを行なうことでΔG<0となるようにします。
相変化のギブス自由エネルギー変化
相変化におけるギブス自由エネルギー変化がどうなるか考えてみましょう。
ここでは液体から気体への蒸発を例にします。
蒸発に必要な熱量は蒸発潜熱ΔHvapで与えられます。
また、蒸発前後でのエントロピー変化ΔSは、エントロピーの定義から
$$ΔS=\frac{ΔH_{vap}}{T}・・・(13)$$
(13)式となります。
したがって、蒸発前後でのギブス自由エネルギー変化ΔGは、
$$ΔG=ΔH_{vap}-T×\frac{ΔH_{vap}}{T}=0・・・(14)$$
(14)式のようにΔG=0となります。
これは蒸発に限った話ではなく、相変化におけるギブス自由エネルギー変化は必ずゼロとなります。
おわりに
ギブス自由エネルギーについて解説しました。
閉鎖系における自発変化の方向を示し、平衡状態に達したときはΔGsys=0となります。
今回紹介した内容以外にも、ギブス自由エネルギーは様々な分野で応用されており、奥が深い状態量です。
