概要
撹拌槽の壁面に内容物を加熱・冷却するための用役を流すスペースを設けることが多いですが、これをジャケットといいます。
撹拌槽の伝熱には主に
- ジャケットによる伝熱
- 内部コイルによる伝熱
- 外部循環熱交換器による伝熱
- 還流コンデンサーによる伝熱
以上のような手法が挙げられますが、ジャケット伝熱はその中で最も一般的です。
ジャケットは内部コイルと違って、槽内部の流動状態に影響を与えることなく温度制御ができる点で優れています。
一方で槽の壁面積分の伝熱面積しか取れないため、スケールアップして撹拌槽が大きくなるほど伝熱能力が不足しがちになります。
その場合には内部コイルや外部循環熱交を追加して伝熱面積を補う等の対策が必要となります。
ジャケットに流す用役は、
- 加熱源:スチーム(120~250℃)、温水(60~120℃)、熱媒油(150~300℃)
- 冷却源:冷却塔冷却水(20~30℃)、チラー水(5~10℃)、ブライン(-20~0℃)
などが主に使用されます。
ジャケットの種類
平板ジャケット
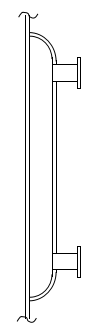
ジャケット内部に仕切りがなく、最も一般的なジャケットです。
低圧スチームで加熱する場合によく使用されます。
平板ジャケットに液体を流すケースもありますが、本来の用途ではなく装置の転用で運転されることが多いです。
最初から液体を流すことがわかっていれば後述するスパイラルジャケットで設計した方がよいでしょう。
相変化のない場合
相変化のない場合のジャケット側の境膜伝熱係数は(1)式で算出できます。
$$\frac{h_{o}D_{e}}{k}=\frac{0.03Re^{0.75}Pr}{1+1.74Re^{-1/8}(Pr-1)}・・・(1)$$
ho:ジャケット側境膜伝熱係数[W/(m2・h)]、De:相当直径[m]
k:熱伝導度[W/(m・h・K)]、Re:レイノルズ数[-]、Pr:プラントル数[-]
"熱交換器設計ハンドブック"より引用
相変化がある場合
ジャケットにスチームを流して凝縮させるときは(2)式で境膜伝熱係数を算出できます。
$$h_{o}=1.47(\frac{{k_{f}}^{3}{ρ_{f}}^{2}g}{{μ_{f}}^{2}})^{1/3}(\frac{4Γ}{μ_{f}})^{-1/3}・・・(2)$$
$$Γ=\frac{W}{πD_{1}}$$
kf:凝縮液の熱伝導度[kcal/(m・h・K)]、ρf:凝縮液の密度[kg/m3]、g:重力加速度[m/s2]
μf:凝縮液の粘度[kg/(m・h)]、W:凝縮量[kg/h]、D1:ジャケット内径[m]
"熱交換器設計ハンドブック"より引用
スパイラルジャケット
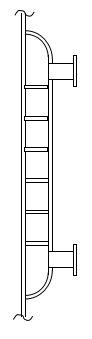
ジャケット内に螺旋状の仕切りを設けたジャケットです。
仕切りによって周方向の流速が増加するため、境膜伝熱係数を大きく出来るのが特徴です。主に冷却水を流す場合に使用されることが多いです。
以下にスパイラルジャケット使用時の境膜伝熱係数の計算式を示します。
$$\frac{h_{o}D_{eq}}{k}=0.025(\frac{D_{eq}uρ}{μ})^{0.8}Pr^{1/3}(\frac{μ}{μ_{w}})^{0.14}・・・(3)$$
ho:ジャケット側境膜伝熱係数[kcal/(m2・h・℃)]、Deq:流路相当直径[m]
k:熱伝導度[kcal/(m・h・℃)]、u:流速[m/s]、ρ:流体密度[kg/m3]
μ:流体粘度[Pa・s]、μw:壁面近傍での流体粘度[Pa・s]、Pr:プラントル数[-]
"工業反応装置"より引用
スパイラルジャケットの流路は円形にはならないので相当直径を使用して近似します。
ただし螺旋状の仕切りは製作上すき間ができるため、多少は流体がショートパスして効率が悪化します。
半割パイプジャケット
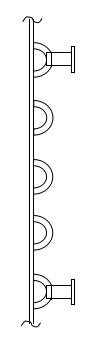
半分に割ったパイプを螺旋状に設置したジャケットです。
スパイラルジャケットと同様に流路が小さいため、境膜伝熱係数を大きく出来ます。
また、高圧スチーム使用時にもよく採用されます。
以下に半割パイプジャケット使用時の境膜伝熱係数の計算式を示します。
$$\frac{h_{o}D_{eq}}{k}=0.026Re^{0.8}Pr^{1/3}(\frac{μ}{μ_{w}})^{0.14}・・・(4)$$
$$D_{eq}=(\frac{8}{3})^{0.5}δ$$
"熱計算ハンドブック"より引用
ただし、(4)式は9,000<Re<40,000、Pr≒6での適用範囲となっています。
レイノルズ数で使用する代表流速はuhの値を使用します。
$$u_{h}=(u_{s}u_{0})^{0.5}+u_{a}$$
$$u_{a}=0.5(2gh_{s}βΔT)^{0.5}$$
$$u_{0}=\frac{M_{M}}{ρ・π{d_{0}}^{2}/4}$$
g:重力加速度[m/s2]、hs:円筒開口部高さ[m]、β:熱膨張係数[1/K]
ΔT:流体の流入流出温度差[K]、MM:流体流量[kg/s]、ρ:流体密度[kg/m3]
d0:半割パイプ直径[m]
また、半割パイプの取付位置によってusの値が変わります。
接線方向に取り付けた半割パイプ
$$u_{s}=\frac{M_{M}}{ρh_{s}δ}$$
δ:開口部幅[m]
半径方向に取り付けた半割パイプ
$$u_{s}=\frac{M_{M}}{ρπd_{BA}δ}$$
dBA:撹拌槽外径[m]
内部ジャケット
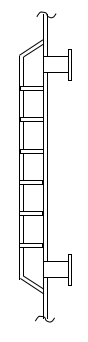
ジャケットは通常、槽壁の外側に設置されますが、この内部ジャケットは槽壁の内側に設置して使用します。
槽本体の板厚が大きい場合は、ジャケットが外側にあると槽壁の熱抵抗が大きくなり伝熱が悪くなります。
そこで、内部に板厚の薄いジャケットを設置することで伝熱性能を向上できます。耐圧計算は槽壁厚みで計算されますから、内部ジャケットの厚みを薄くしても問題ありません。
おわりに
撹拌槽のジャケットについて解説しました。
槽内側の伝熱が悪いのはプロセス上の都合もあるので仕方ないですが、ジャケット側の伝熱が悪くて足を引っ張ることだけは避けましょう。
適切な形状と用役を選定し、プロセス側よりも十分大きい境膜伝熱係数を確保することが重要です。
