概要
充填塔の設計において、過度なエントレインメントやフラッディングが起こるかどうかを確認する指標としてよく使用される因子がF-factor(F因子)です。
$$F=u\sqrt{ρ_{V}}$$
F:F-factor[Pa0.5]、u:空塔速度[m/s]、ρV:ガス密度[kg/m3]
F-factorは上式で表されます。
F-factorを求めること自体は簡単です。
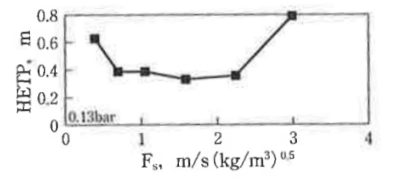
F-factorは例えば上図のように縦軸HETP、横軸F-factorのグラフで使用されます。
このグラフは充填物の性能を示すもので、縦軸のHETPが低いほど性能が良く、充填高さが低くなることを意味します。
たたし、充填物が性能を発揮するには適正な運転範囲に入っている必要があります。
適性な運転範囲かどうかは横軸のF-factorの値で大まかにわかります。
目安としてF-factorが1より小さいとガス流速が小さいため、HETPは高くなる傾向にあります。
一方でF-factorが2.5~3.0を超えてくると、ガス流速が大きくなり過ぎてエントレインメントやフラッディングを起こし効率が低下するためHETPは高くなります。
そのため、一般的には1≦F-factor≦2.5の範囲であれば安定的に運転できるとされています。
F-factorの導出
F-factorは棚段塔のエントレインメントが許容できる蒸気速度を求める式である、Souders-Brown式を変形すれば導出できます。
$$u_{c}=K\sqrt{\frac{ρ_{L}-ρ_{V}}{ρ_{V}}}$$
uc:許容ガス速度、K:定数
ρL:液密度、ρV:ガス密度
上式がSouders-Brown式です。
ガス密度に比べて液密度の方が圧倒的に大きく、ρL>>ρVとすると、
$$u_{c}=K\sqrt{\frac{ρ_{L}}{ρ_{V}}}$$
となります。
また液密度は1000kg/m3前後で、物質による違いが少ないことから一定値とみなし定数に含めると、
$$u_{c}=K'\sqrt{\frac{1}{ρ_{V}}}$$
となります。
この式を変形すると、
$$K'=F=u\sqrt{ρ_{V}}$$
となり、F-factorの形となりました。
