概要
この記事ではエネルギー管理士(熱分野)の出題分野である、流体工学の基礎について解説します。
流体工学の基礎は課目Ⅱ"熱と流体の流れの基礎"の中で、大問4問中1問出題されています。
課目Ⅱの中では計算問題が少なく、かつ難易度も比較的簡単です。普段実務で配管の流量計算、圧損計算をやっている方にとっては得点源となるでしょう。
高圧ガス甲種機械との被り
エネルギー管理士の"流体工学の基礎"は、高圧ガス甲種機械の検定試験における"流体の流れ"の分野と内容がかなり被っています。
-
【流体の流れ】高圧ガス甲種機械：検定試験の出題分野を解説
この記事では高圧ガス甲種機械の出題分野である、流体の流れについて解説します。他の大問と比較して、流体の流れは簡単なので確実に点を取りたいところです。
続きを見る
上の記事に高圧ガス甲種機械の"流体の流れ"の出題内容を解説していますので、まずはこの内容を把握しましょう。
それだけで、エネルギー管理士"流体工学の基礎"の出題内容の半分くらいはカバーできます。
その他、エネルギー管理士で出題されやすそうな内容を以下で解説しています。
圧力損失
エネルギー管理士の試験なので、エネルギー損失である圧力損失の内容は特に頻出です。
管摩擦係数f
層流
ハーゲン・ポアズイユの式である(1)式と、ダルシー・ワイズバッハの式である(2)式との比較で層流の管摩擦係数fが導出されます。
$$ΔP=\frac{32μL\bar{u}}{d^{2}}・・・(1)$$
$$ΔP=f\frac{ρu^{2}}{2}\frac{L}{d}・・・(2)$$
(1)、(2)式からΔPを消去し、残った変数をレイノルズ数Reでおくと、
$$f=\frac{64}{Re}・・・(3)$$
管摩擦係数fは(3)式で表されます。
エネルギー管理士の分野では、機械工学に寄っていることからダルシー・ワイズバッハの式が使用されていますが、私のように化学工学専攻の方は(4)式のファニングの式で覚えているでしょう。
$$ΔP=4f\frac{ρu^{2}}{2}\frac{L}{d}・・・(4)$$
係数として4がかかっているかの違いではありますが、エネルギー管理士試験では(2)式で考えるようにしましょう。
乱流
乱流の場合は様々な管摩擦係数の算出式があります。しかし、あまり複雑な式は試験に出にくいでしょう。
過去に出題されたことのある式としては、ブラジウスの式である(5)式が挙げられます。
$$f=\frac{0.316}{Re^{\frac{1}{4}}}・・・(5)$$
乱流で管壁が滑らかな場合に(5)式を適用できます。
ムーディー線図
管摩擦係数とレイノルズ数Re及び管壁の粗さεの関係を示した図をムーディー線図といいます。
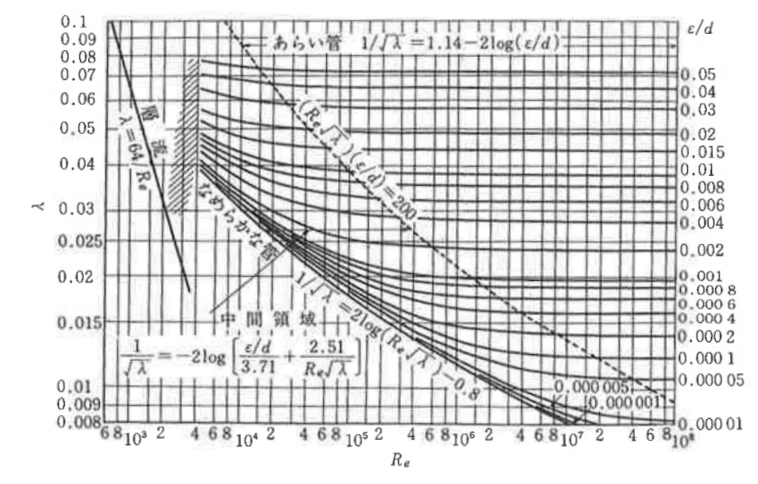"機械工学便覧 基礎編α4 流体工学"より引用
ムーディー線図から数値を読み取る問題はあまり出題されたことはありませんが、語句はよく問われます。
各種管路要素の圧力損失
配管は直管だけで構成されているわけではなく、実際は曲がり部や拡大・縮小部、弁などの様々な形状をした流路が間にあります。
それらの特殊形状部では別途圧力損失を計算する必要があります。
計算式としては、
$$ΔP[Pa]=K\frac{ρv^{2}}{2}・・・(6)$$
$$h_{l}[m]=K\frac{v^{2}}{2g}・・・(7)$$
K：損失係数[-]
(6)式の圧力損失ΔPの形か、もしくは(7)式のヘッドhl[m]の形で計算することが多いです。
あとは損失係数Kをどのようにして求めるかですが、各形状で計算方法が異なります。
詳細は以下の記事で解説しています。
-
配管流路【圧力損失】の計算方法を形状ごとに解説
流体が壁面との摩擦や流体同士の摩擦によってエネルギーを損失することを圧力損失といいます。この記事では実務で計算する頻度の多い配管流路の圧力損失について計算方法を紹介します。
続きを見る
ポンプ
駆動動力
ポンプの駆動動力は式の形を答える問題や、計算問題等の様々な形で出題されやすいのでぜひ覚えておきましょう。
$$P=\frac{MgH}{η}=\frac{ρgQH}{η}・・・(8)$$
P：ポンプの駆動動力[W]、M：吐出し質量流量[kg/s]、Q：吐出し体積流量[m3/s]
ρ：液体密度[kg/m3]、g：重力加速度[m/s2]、H：全揚程[m]、η：ポンプ効率[-]
(8)式の形で計算できます。
比速度
羽根車を相似形でスケールを変化させる場合、比速度Nsを一定とすることで流れが相似となります。
$$N_{s}=N\frac{\sqrt{Q}}{H^{\frac{3}{4}}}・・・(9)$$
N：回転数[rpm]、H：全揚程[m]、Q：吐出し量[m3/min]
式の形が出題されることがありますので、覚えておきましょう。
性能曲線
ポンプの全揚程、軸動力、効率と吐出し量の関係を線図にしたものを性能曲線といいます。
ポンプの種類や型番によって性能曲線の形が変わるので、どのような性能になるのか一般論として覚えにくい内容です。
全揚程H-吐出量Qの性能曲線である、H-Q曲線については以下の記事で詳細を解説しています。
-
【H-Q曲線】ポンプの性能曲線を解説：単独運転・直列運転・並列運転の違いは？
ポンプの揚水性能を表わす手法として、縦軸に全揚程H、横軸にポンプの吐出し量Qを取ったものをH-Q曲線と言います。この記事ではH-Q曲線が単独運転、直列運転、並列運転でどう変化するかを解説しています。
続きを見る
キャビテーション
ポンプの運転で問題となる現象の1つとして、キャビテーションが挙げられます。
キャビテーションとは、ポンプ内で局所的に負圧となり液体の飽和蒸気圧を下回ると気泡が発生する現象です。
気泡が発生すると騒音や振動の原因となり、さらに気泡が羽根車に衝突すると機械的な損傷を与えます。
したがって、ポンプの設計時にはNPSHと呼ばれる指標を守り設計することで、キャビテーションの発生を抑制することができます。
NPSHについては以下の記事で解説しています。
-
【NPSH】を解説：キャビテーションを回避できるポンプ揚程
ポンプの運転において、キャビテーションを発生させずに運転できるかどうかを判断するための指標をNPSH(Net Positive Suction Head)といいます。
続きを見る
サージング
ポンプの運転で問題となる現象の1つとして、サージングが挙げられます。
サージングは、ポンプの運転中に周期的な圧力変動が発生し吸込み側・吐出し側の配管で振動や騒音が起こる現象です。
サージングが発生する条件としてはいくつかあり、以下の記事で解説しています。
-
【サージング】を解説：ポンプ・圧縮機の周期的圧力変動
遠心ポンプ・圧縮機の運転中に、周期的な圧力変動が発生し吸込み側・吐出し側の配管で振動や騒音が起こる現象をサージングといいます。この記事ではサージングの発生条件と防止法について解説しています。
続きを見る
水撃作用
ポンプの運転で問題となる現象の1つとして、水撃作用(ウォーターハンマー)が挙げられます。
出題されるときは回答の選択肢にキャビテーション、サージング、水撃作用が含まれることが多いので、混同しないようにしましょう。
水撃作用は、出口の弁を急閉して流れをせき止めたときに、上流側の流体の速度が急激に変化し圧力上昇する現状です。
例えば停電等によりポンプが急停止した場合に起こり、発生した高圧力により配管を破壊することがあります。
水撃作用の防止方法としては、
- ポンプにフライホイールを取り付け、停電時にゆっくりと停止するようにする。
- 停電時に作動する自動水圧調節弁を付け、圧力の急激な上昇を防ぐ。
- サージタンクを取り付け、圧力の急激な上昇を防ぐ。
などが挙げられます。
送風機
過去の傾向から言うと、ポンプと比較して出題されにくいです。
送風機の動力計算はポンプより難しく、ポンプの方が試験に出すにはちょうどいい難易度なのでしょう。
しかし送風機特有の事項は過去に出題されたことがあり、多少は目を通しておくことをオススメします。
風量制御方法
特に省エネ効果が高い制御方法を覚えておいた方がよいでしょう。
吐出しダンパによる制御
送風機の吐出しダンパ(吐出し弁)を絞ることで抵抗を増加させて風量制御する方法です。
風量制御を簡便に行うことができますが、増加させた抵抗はすべて圧力損失となります。
そのため、大型機に使用するとエネルギーロスが大きいため、小型機に使用するのがよいでしょう。
吸込みダンパによる制御
送風機の吸込みダンパ(吸込み弁)を絞ることで抵抗を増加させて風量制御する方法です。
吸込み側と吐出し側の両方の圧力が低下するため、吐出しダンパ制御よりも広い運転範囲を得ることができます。
インレットガイドベーン(IGV)制御
羽根車直前の吸込みベーンをリンク機構により開閉することで、流体に羽根車の回転と同方向の予旋回を与えます。
これにより羽根車の理論仕事そのものを減少させて流量制御する方法です。
回転速度制御に匹敵するほどに部分負荷時の駆動動力を軽減できます。
回転速度制御
羽根車の回転速度を変化させることで風量を制御する方法です。
一般に、風量制御方法の中で最も省エネルギー効果が高く多用されています。
軸流送風機の動翼可変ピッチ制御
羽根車の動翼の取付角を変えて風量を制御する方法です。
軸流送風機に特有な制御方法で、広範な風量に対して所要駆動動力を小さくできます。
台数制御
風量増加を目的とする場合に、送風機の台数を増やして風量を制御する方法です。
並列運転、直列運転等の運転方法があり、ポンプの場合と考え方は変わりません。
以下の記事で、並列運転、直列運転について解説しています。
-
【H-Q曲線】ポンプの性能曲線を解説：単独運転・直列運転・並列運転の違いは？
ポンプの揚水性能を表わす手法として、縦軸に全揚程H、横軸にポンプの吐出し量Qを取ったものをH-Q曲線と言います。この記事ではH-Q曲線が単独運転、直列運転、並列運転でどう変化するかを解説しています。
続きを見る
旋回失速
羽根に対する気体の流入角度がある程度以上になると、羽根の出口付近で流れの剥離が生じて送風機の性能が低下する現象です。
旋回失速では失速状態にある羽根と正常な羽根が混在しており、運転音に異常が認めづらく外部から気づかないことが多いです。
しかし、旋回失速は羽根に繰り返し応力を及ぼすため、羽根の疲労破壊に繋がる可能性があります。
流量測定
ベンチュリー管
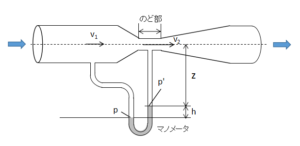
上図のようにゆるやかな縮小部と拡大部を持つ管をベンチュリー管と呼びます。
ベンチュリー管は動圧と静圧の異なる箇所を作り出し、各々の箇所の静圧差を測定することで流速を測定できます。
通常は、縮小前の箇所と縮小後ののど部にマノメータ(差圧計)が付いており、静圧差を測定します。
詳細は以下の記事で解説しています。
-
【ベンチュリー管】を解説：流路の拡大縮小による流量測定
上図のようにゆるやかな縮小部と拡大部を持つ管をベンチュリー管と呼びます。ベンチュリー管は動圧と静圧の異なる箇所を作り出し、各々の箇所の静圧差を測定することで流速及び流量を測定できます。
続きを見る
ピトー管
上図のように全圧と静圧を測定することで流体の流速を測定する装置をピトー管といいます。
ベンチュリ管と同様に流速を測定することができます。
詳細は以下の記事で解説しています。
-
【ピトー管】を解説：簡便な流速測定法
全圧と静圧を測定することで流体の流速を測定する装置をピトー管といいます。測定した全圧と静圧から動圧を算出することができます。この計算はベルヌーイの定理から導くことができ、動圧は流速の2乗に比例することが知られています。
続きを見る
おわりに
課目Ⅱの流体工学の基礎について解説しました。
他の資格の出題範囲と被っている箇所が多いです。エネルギー管理士が初めて受ける資格試験でなければ、他の資格勉強で得た知識である程度カバーできると思います。