【課目Ⅱ：熱力学の基礎】エネルギー管理士(熱分野)の出題分野を解説

概要

この記事ではエネルギー管理士(熱分野)の出題分野である、熱力学の基礎について解説します。

熱力学の基礎は課目Ⅱ"熱と流体の流れの基礎"の中で、大問4問中2問出題されておりウェイトが高い分野です。

どの課目も6割以上取れば合格なのですが、熱力学の基礎は全200点中100点の配点があるため、合格するには避けては通れない分野です。

むしろこの分野を重点的に勉強し満点を取ることができれば、余裕をもって合格することができるでしょう。

理想気体の状態変化・サイクル

大問2問中の1問は理想気体の状態変化やサイクルに関連する内容が出題されることが多いです。  

理想気体の状態方程式

理想気体の状態方程式はまず最初に覚えるべき基本の式です。

$$PV=mRT・・・(1)$$

P：圧力[Pa]、V：体積[m³]、m：質量[kg]

R：気体定数(ガス定数)[J/(kg・K)]、T：温度[K]

化学系の分野で状態方程式を習うとPV=nRTの形で覚えると思います。

反応が起こる場合にはモル数nが重要だからですね。 一方でエネルギー管理士の熱力学の分野では、モル数nはそこまで重要ではないので質量mをベースにした形となっています。

加えて、気体定数は問題文で与えられると思いますが、単位と値がモル数ベースの場合と異なるので注意しましょう。

定圧比熱・定容比熱

比熱は温度変化させる際の条件によって異なる値を示します。

液体や固体の場合は条件による比熱の差異が小さいため、通常は条件によらずほぼ一定値とみなしています。

しかし気体の場合は差異が大きいため区別して考慮しています。試験では特に定圧比熱・定容比熱に関して出題されることが多いです。

$$C_{p}-C_{v}=R・・・(2)$$

$$κ=\frac{C_{p}}{C_{v}}・・・(3)$$

C_p：定圧比熱[kJ/(kg・K)]、C_v：定容比熱[kJ/(kg・K)]

κ：比熱比[-]

とりあえず覚えるべきは上の(2)、(3)式です。 比熱比κは問題で与えられると思いますが、参考までに2原子分子では1.4という値になります。

熱容量については以下の記事で詳細に解説しています。

等容変化

ボイル・シャルルの法則から

ボイル・シャルルの法則から、V₁=V₂とすると、

$$\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}・・・(4)$$

P₁,P₂：状態1,2での圧力[Pa]、T₁,T₂：状態1,2での温度[K]

(4)式が成り立ちます。 また、P-V線図上で等容変化を表わすと下図のように直線となります。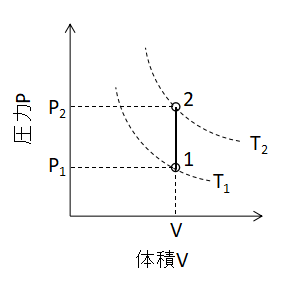  

熱力学の第一法則から

体積Vが一定とみなせるためΔV＝0となり、系が外にする仕事W₁₂=0となります。 したがって、

$$Q_{12}=ΔU+W_{12}=mC_{v}(T_{2}-T_{1})・・・(5)$$

Q₁₂：熱量[J]、ΔU：内部エネルギー変化[J]、W₁₂：仕事[J]

(5)式となり、外部から加えられた熱量は全て内部エネルギーの増加に使用されます。

比エントロピー計算

等容変化の比エントロピー計算式は、

$$Δs=s_{2}-s_{1}=C_{v}{\rm{ln}}\frac{T_{2}}{T_{1}}・・・(6)$$

s₁,s₂：状態1,2での比エントロピー[J/(kg・K)]、T₁,T₂：状態1,2での温度[K]

C_v：定容比熱[J/(kg・K)]

(6)式で表されます。 また、T-S線図上で等容変化を表わすと下図のようになります。  

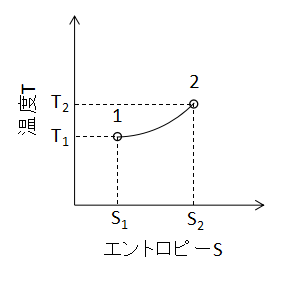
等圧変化

ボイル・シャルルの法則から

ボイル・シャルルの法則から、P₁=P₂とすると、

$$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}・・・(7)$$

V₁,V₂：状態1,2での体積[m³]、T₁,T₂：状態1,2での温度[K]

(7)式が成り立ちます。 また、P-V線図上で等圧変化を表わすと下図のように直線となります。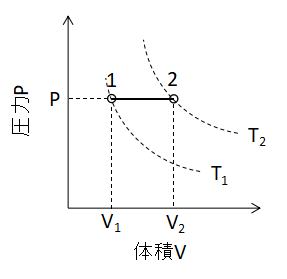  

熱力学の第一法則から

圧力pが一定とみなせるため、系が外にする仕事W₁₂[J]は、

$$\begin{align}W_{12}&=\int_{V1}^{V2}pdV=p[V]^{V_{2}}_{V_{1}}\\& =p(V_{2}-V_{1})・・・(8)\end{align}$$

(8)式のように簡単に積分して求めることができます。

また熱量Q₁₂は、

$$Q_{12}=ΔU+W_{12}=mC_{p}(T_{2}-T_{1})・・・(9)$$

(9)式となります。

比エントロピー計算

等圧変化の比エントロピー計算式は、

$$Δs=s_{2}-s_{1}=C_{p}{\rm{ln}}\frac{T_{2}}{T_{1}}・・・(10)$$

s₁,s₂：状態1,2での比エントロピー[J/(kg・K)]、T₁,T₂：状態1,2での温度[K]

C_p：定圧比熱[J/(kg・K)]

(10)式で表されます。 また、T-S線図上で等容変化を表わすと下図のようになります。    

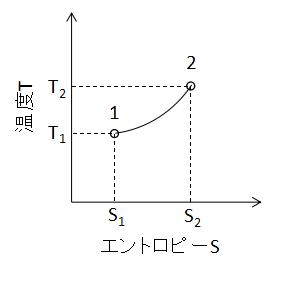
等容変化と等圧変化のT-S線図は見た目がほとんど同じであるため、変化の判別にはP-V線図等の別の情報が必要となるでしょう。

等温変化

ボイル・シャルルの法則から

ボイル・シャルルの法則から、T₁=T₂とすると、

$$P_{1}V_{1}=P_{2}V_{2}・・・(11)$$

(11)式が成り立ちます。 また、P-V線図上で等温変化を表わすと下図のような曲線となります。

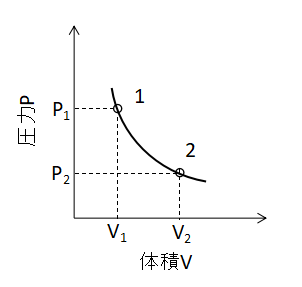
熱力学の第一法則から

系が外にする仕事Wは、

$$W_{12}=\int_{V1}^{V2}PdV=\int_{V1}^{V2}\frac{nRT}{V}dV・・・(12)$$

(12)式で表されます。

ここで、等温変化では温度Tが圧力P、体積Vに依存せず一定とみなせるため、(10)式を積分することができます。

$$\begin{align}W_{12}&=mRT[{\rm{ln}}V]^{V_{2}}_{V_{1}}\\&
=mRT{\rm{ln}}(\frac{V_{2}}{V_{1}})=mRT{\rm{ln}}(\frac{P_{1}}{P_{2}})・・・(11)\end{align}$$

積分すると(11)式となります。

また温度一定であるため内部エネルギー変化ΔU=0となることから熱量Q₁₂は、

$$Q_{12}=ΔU+W_{12}=W_{12}・・・(13)$$

(13)式となります。

比エントロピー計算

等温変化の比エントロピー計算式は、

$$Δs=s_{2}-s_{1}=R{\rm{ln}}\frac{V_{2}}{V_{1}}・・・(14)$$

(14)式で表されます。

加えて、エントロピーの定義式から、

$$Δs=s_{2}-s_{1}=\frac{Q_{12}}{T}・・・(15)$$

(15)式と表すこともできます。

また、T-S線図上で等温変化を表わすと下図のようになります。    

断熱変化

断熱変化をP-V線図で表すと上図のようになります。

1→2への変化前後でP、V、T全てが変化するため、P-V線図においてはあまり特徴的ではありません。

熱力学の第一法則から

断熱変化の場合は、熱力学の第一法則とマイヤーの関係から、次の(16)式が導出できます。

$$P_{1}V_{1}^{κ}=P_{2}V_{2}^{κ}・・・(16)$$

κ：比熱比[-]

断熱変化における仕事Wは(16)式を使用して導出します。(16)式から

$$PV^{κ}=P_{1}V_{1}^{κ}$$

$$P=P_{1}(\frac{V_{1}}{V})^{κ}$$

と変形して仕事の定義式に代入します。

$$\begin{align}W_{12}&=\int_{V1}^{V2}P_{1}(\frac{V_{1}}{V})^{κ}dV
=P_{1}V_{1}^{κ}[-\frac{1}{κ-1}V^{-(κ-1)}]^{V_{2}}_{V_{1}}\\&
=\frac{P_{1}V_{1}^{κ}}{κ-1}(V_{1}^{-(κ-1)}-V_{2}^{-(κ-1)})=\frac{P_{1}V_{1}}{κ-1}\Biggl(\frac{V_{1}^{-(κ-1)}}{V_{1}^{-(κ-1)}}-\frac{V_{2}^{-(κ-1)}}{V_{1}^{-(κ-1)}}\Biggr)\\&
=\frac{P_{1}V_{1}}{κ-1}\Bigl(1-(\frac{V_{1}}{V_{2}})^{κ-1}\Bigr)=\frac{P_{1}V_{1}}{κ-1}\Bigl(1-(\frac{P_{2}}{P_{1}})^{\frac{κ-1}{κ}}\Bigr)・・・(17)\end{align}$$

最終的に(17)式の形となります。

また熱量Qは断熱変化であるためQ=0となり、

$$ΔU=-W_{12}・・・(17)$$

(17)式となります。

比エントロピー計算

等圧変化の比エントロピー計算式は、Q₁₂=0であるためエントロピーの定義式(15)式から、

$$Δs=s_{2}-s_{1}=0・・・(18)$$

(18)式となります。

また、T-S線図上で断熱変化を表わすと下図のようになります。    

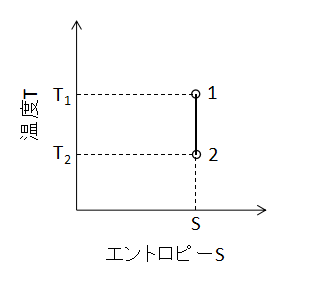
熱機関

大問2問中のもう1問は熱機関のサイクルに関連する内容が出題されることが多いです。  

理想気体の状態変化の応用的な位置付けですが、サイクルの状態変化ごとに考えて式変形すれば解けるはずです。

また、参考書等にはいくつものサイクルの種類が載っていますが、式の形が複雑で難しいサイクルは出題されにくい気がします。

ここでは比較的簡単で出題されやすいサイクルを紹介します。

最高効率のサイクル

カルノーサイクル

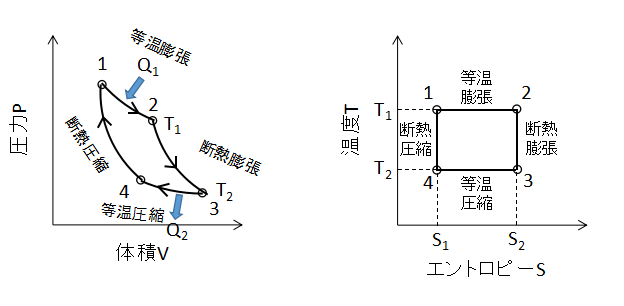
上図にカルノーサイクルのPV線図、TS線図を示します。

2つの等温変化と2つの断熱変化を組み合わせたサイクルで、理論上最も熱効率が良いとされています。

等温膨張で加えられる熱量をQ₁、等温圧縮で放出される熱量をQ₂とすると、

$$Q_{1}=mRT_{1}{\rm{ln}}\frac{P_{1}}{P_{2}}・・・(19)$$

$$Q_{2}=mRT_{1}{\rm{ln}}\frac{P_{4}}{P_{3}}・・・(20)$$

(19)、(20)式となります。

ここで、理想気体の状態方程式(1)式と、断熱変化の関係式(16)式から、

$$\frac{P_{1}}{P_{2}}=\frac{P_{4}}{P_{3}}・・・(21)$$

(21)式を導くことができます。

(19)、(20)、(21)式から、

$$\frac{Q_{1}}{Q_{2}}=\frac{T_{1}}{T_{2}}・・・(22)$$

(22)式となります。

したがって、サイクルの熱効率ηは、

$$η=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}・・・(23)$$

(23)式で表されます。

(23)式から、カルノーサイクルの熱効率は高温側熱源と低温側熱源の温度のみで決定されることがわかります。

ガスサイクル

オットーサイクル

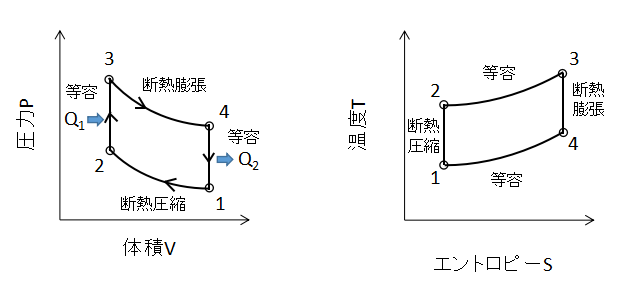
上図にオットーサイクルのPV線図、TS線図を示します。

2つの等容変化と2つの断熱変化を組み合わせたサイクルです。

等容変化で加えられる熱量をQ₁、放出される熱量をQ₂とすると(5)式から、

$$Q_{1}=mC_{v}(T_{3}-T_{2})・・・(24)$$

$$Q_{2}=mC_{v}(T_{4}-T_{1})・・・(25)$$

(24)、(25)式となります。

したがって、サイクルの熱効率ηは、

$$η=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{4}-T_{1}}{T_{3}-T_{2}}・・・(26)$$

(26)式で表されます。

また、オットーサイクルは圧縮比εで熱効率ηを表わすことがあります。

1→2の変化は断熱変化であるため、(16)式とボイル・シャルルの法則から、

$$T_{2}=T_{1}(\frac{V_{1}}{V_{2}})^{κ-1}・・・(27)$$

(27)式で表されます。

ここで圧縮比εは、

$$ε=\frac{V_{1}}{V_{2}}=\frac{V_{4}}{V_{3}}・・・(28)$$

(28)式で表されるため、(27)式は

$$T_{2}=T_{1}ε^{κ-1}・・・(29)$$

(29)式となります。

次に、2→3は等容変化であるため(4)式から、

$$T_{3}=T_{2}\frac{P_{3}}{P_{2}}=T_{1}ε^{κ-1}\frac{P_{3}}{P_{2}}・・・(30)$$

(30)式となります。

次に、3→4は断熱変化であるため同様に、

$$T_{4}=T_{3}(\frac{V_{3}}{V_{4}})^{κ-1}=T_{3}(\frac{1}{ε})^{κ-1}・・・(31)$$

(31)式となります。これに(30)式を代入して、

$$T_{4}=T_{1}\frac{P_{3}}{P_{2}}・・・(32)$$

(32)式となります。

最後に(29)、(30)、(32)式を(26)式に代入すると、

$$η=1-\frac{T_{1}\frac{P_{3}}{P_{2}}-T_{1}}{T_{1}ε^{κ-1}\frac{P_{3}}{P_{2}}-T_{1}ε^{κ-1}}=1-\frac{1}{ε^{κ-1}}・・・(33)$$

(33)式となり、圧縮比εで表すことができました。

したがって、オットーサイクルの熱効率は圧縮比εと比熱比κから決定されます。

圧縮比εを大きくするほど熱効率が向上しますが、あまりにも極端に圧縮比を大きくし過ぎると異常燃焼が発生する可能性があるので注意です。

ブレイトンサイクル

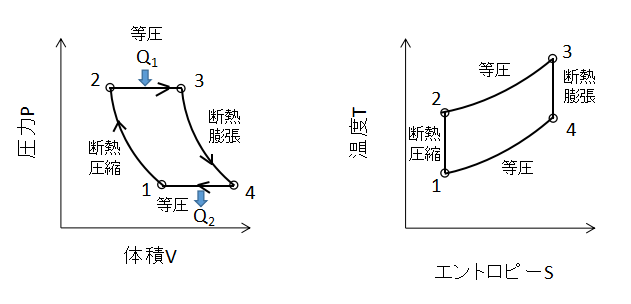
上図にブレイトンサイクルのPV線図、TS線図を示します。

2つの等圧変化と2つの断熱変化を組み合わせたサイクルです。

等圧変化で加えられる熱量をQ₁、放出される熱量をQ₂とすると(9)式から、

$$Q_{1}=mC_{p}(T_{3}-T_{2})・・・(34)$$

$$Q_{2}=mC_{p}(T_{4}-T_{1})・・・(35)$$

(34)、(35)式となります。

したがって、サイクルの熱効率ηは、

$$η=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{4}-T_{1}}{T_{3}-T_{2}}・・・(36)$$

(36)式で表されます。

また、ブレイトンサイクルは圧力比φで熱効率ηを表わすことがあります。

1→2、3→4の変化は断熱変化であるため、(16)式とボイル・シャルルの法則から、

$$\frac{T_{1}}{T_{2}}=(\frac{P_{1}}{P_{2}})^{\frac{κ-1}{κ}}・・・(37)$$

$$\frac{T_{4}}{T_{3}}=(\frac{P_{4}}{P_{3}})^{\frac{κ-1}{κ}}・・・(38)$$

(37)、(38)式で表されます。

ここで圧力比φは、

$$φ=\frac{P_{2}}{P_{1}}=\frac{P_{3}}{P_{4}}・・・(39)$$

(39)式で表されるため、(37)、(38)式は

$$T_{1}=T_{2}(\frac{1}{φ})^{\frac{κ-1}{κ}}・・・(40)$$

$$T_{4}=T_{3}(\frac{1}{φ})^{\frac{κ-1}{κ}}・・・(41)$$

(40)、(41)式となります。

最後に(40)、(41)式を(36)式に代入すると、

$$η=1-\frac{T_{3}(\frac{1}{φ})^{\frac{κ-1}{κ}}-T_{2}(\frac{1}{φ})^{\frac{κ-1}{κ}}}{T_{3}-T_{2}}=1-(\frac{1}{φ})^{\frac{κ-1}{κ}}・・・(42)$$

(42)式となり、圧力比φで表すことができました。

したがって、ブレイトンサイクルの熱効率は圧力比φと比熱比κから決定されます。

蒸気サイクル

ランキンサイクル

熱機関の分野では出題頻度の高いサイクルですので、ぜひ覚えておきましょう。

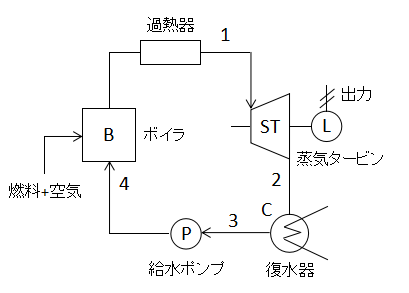
上図にランキンサイクルの構成要素を示します。各要素と後述する線図を照らし合わせて覚えるのがよいでしょう。

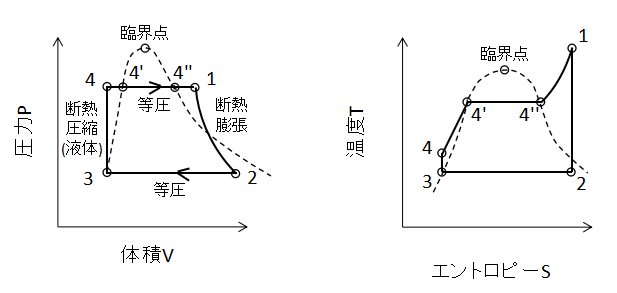
上図にランキンサイクルのPV線図、TS線図を示します。

1→2(蒸気タービンでの可逆断熱膨張)

1の過熱蒸気が可逆断熱膨張してタービンを回すことで仕事をし、2の湿り蒸気となります。このときの仕事W_t[kW]は、

$$W_{t}=m'(h_{1}-h_{2})・・・(43)$$

m'：質量流量[kg/s]、h₁,h₂：状態1,2での比エンタルピー[kJ/kg]

(43)式で表されます。

2→3(復水器での等圧冷却)

2の湿り蒸気を冷却し、蒸気を完全に凝縮させます。このときの交換熱量Q₂[kW]は、

$$Q_{2}=m'(h_{2}-h_{3})・・・(44)$$

(44)式で表されます。

3→4(給水ポンプでの可逆断熱圧縮)

3の飽和水をポンプで加圧します。このときの仕事W_p[kW]は、

$$W_{p}=m'(h_{4}-h_{3})・・・(45)$$

(45)式で表されます。

4→1(ボイラ・過熱器での等圧加熱)

4の加圧水をボイラー及び過熱器で加熱して過熱蒸気とします。このときの交換熱量Q₁[kW]は、

$$Q_{1}=m'(h_{1}-h_{4})・・・(46)$$

(46)式で表されます。

このランキンサイクルの熱効率ηは、

$$η=1-\frac{Q_{2}}{Q_{1}}=\frac{(h_{1}-h_{2})-(h_{4}-h_{3})}{h_{1}-h_{4}}$$

となります。

ただ、ランキンサイクルでは1→2でタービンから取り出せる仕事に比べて、3→4でポンプで加圧する仕事は無視できるほど小さいため、h₄≒h₃とすることができます。

したがって熱効率は、

$$η≒\frac{h_{1}-h_{2}}{h_{1}-h_{3}}・・・(47)$$

(47)式で表されます。

この熱効率の計算は出題頻度が高いので覚えておきましょう。

また、他に出題頻度が高いのが、2の湿り蒸気の乾き度から比エンタルピーを計算し、タービンの出力を計算する問題です。

乾き度は比エントロピーから計算することが多いです。

1→2は可逆断熱過程で、TS線図からエントロピーが一定であることがわかります。したがって、

$$s_{1}=s_{2}・・・(48)$$

s₁,s₂：状態1,2の比エントロピー[kJ/(kg・K)]

(48)式が成り立ちます。

また、2の湿り蒸気の比エントロピーは、

$$s_{2}=s'+x_{ad}(s''-s')・・・(49)$$

s'：状態2の圧力での飽和水の比エントロピー[kJ/(kg・K)]

s''：状態2の圧力での飽和蒸気の比エントロピー[kJ/(kg・K)]

x_ad：乾き度[-]

(49)式となります。

(48)、(49)式からs₂を消去することで、

$$x_{ad}=\frac{s_{1}-s'}{s''-s'}・・・(50)$$

(50)式となり、乾き度x_adを算出することができます。

次に湿り蒸気の比エンタルピーh₂は、

$$h_{2}=h'+x_{ad}(h''-h')・・・(51)$$

h'：状態2の圧力での飽和水の比エンタルピー[kJ/kg]

h''：状態2の圧力での飽和蒸気の比エンタルピー[kJ/kg]

(51)式で計算できます。

最後にタービンの出力W_t[kW]は(43)式から計算することができます。

$$W_{t}=m'(h_{1}-h_{2})・・・(43)$$

再生サイクル

広義的にはランキンサイクルの一種ですが、この記事では前述した基本的なランキンサイクルと区別して再生サイクルと呼んでいます。

ランキンサイクルでは復水器で冷却水に捨てる熱量が多いという課題が挙げられます。

そこで、タービンで膨張途中の蒸気を一部取り出し、ボイラ前の給水を予熱することで熱効率の向上を図ったのが再生サイクルです。

出題頻度は数年に1度といったところで高くはないですが、全く勉強していないと解くのが難しいと思います。他の分野の勉強時間との兼ね合いで余裕があれば勉強しておきましょう。

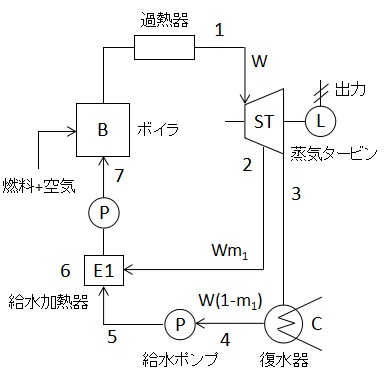
上図に1段再生サイクルの構成要素を示します。

給水加熱器を新たに設置し、2でタービンから一部取り出した蒸気と5の給水を混合して加熱しているのがポイントです。

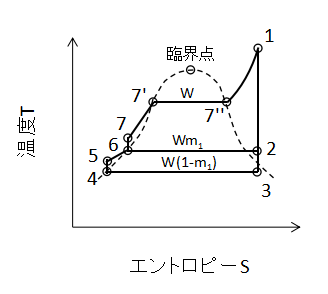
上図に1段再生サイクルのTS線図を示します。

2からWm₁[kg/s]の蒸気を6の給水加熱器に戻し混合することで3の復水器に捨てる熱量が削減できます。

出題されるとすれば、再生サイクルの熱効率を求める問題でしょう。

ランキンサイクルと同様にポンプの仕事が無視できるとすると、ボイラー及び過熱器で与える加熱量の合計Q₁は、

$$Q_{1}=W(h_{1}-h_{6})・・・(52)$$

W：質量流量[kg/s]、h₁,h₆：状態1,6での比エンタルピー[kJ/kg]

(52)式で表されます。

また、復水器に捨てる熱量Q₂は、

$$Q_{2}=W(1-m_{1})(h_{3}-h_{4})・・・(53)$$

m₁：抽気蒸気割合[-]、h₃,h₄：状態3,4での比エンタルピー[kJ/kg]

(53)式となります。

したがって、熱効率ηは、

$$η=1-\frac{Q_{2}}{Q_{1}}=1-\frac{(1-m_{1})(h_{3}-h_{4})}{h_{1}-h_{6}}・・・(54)$$

(54)式となります。

再熱サイクル

同様にランキンサイクルと区別して再熱サイクルと呼んでいます。

ランキンサイクルの熱効率は初圧を上げるほど向上しますが、タービン出口での湿り蒸気の乾き度が低下する課題が挙げられます。

そこで、タービンで膨張途中の蒸気を取り出し、再加熱したあとにタービンに戻すことで乾き度の低下を抑制したのが再生サイクルです。

再生サイクルと同様に出題頻度は数年に1度といったところで、余裕があれば勉強しておきましょう。

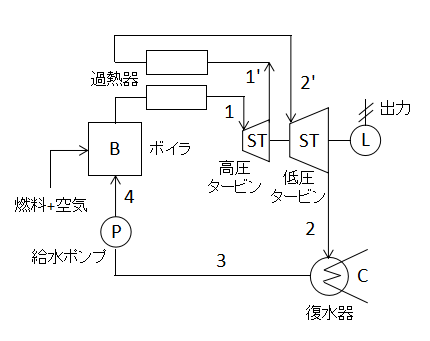
上図に1段再熱サイクルの構成要素を示します。

高圧タービンから蒸気を取り出し、再加熱してから低圧タービンに戻しているのがポイントです。

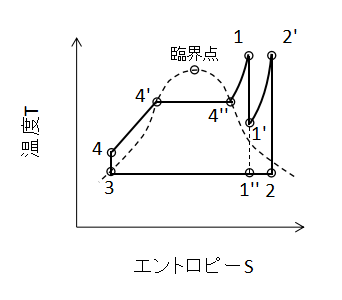
上図に1段再生サイクルのTS線図を示します。

再熱しない場合は湿り蒸気の乾き度は1''となりますが、再熱した場合は2となり、乾き度が増加していることがわかります。

試験には同様に、サイクルの熱効率を求める問題が出題されるでしょう。

同様にポンプの仕事が無視できるとすると、ボイラー及び過熱器で与える加熱量の合計Q₁は、

$$Q_{1}=W((h_{1}-h_{3})+(h_{2'}-h_{1'}))・・・(55)$$

(55)式で表されます。

また、タービンで発生する仕事W_tは、

$$W_{t}=W((h_{1}-h_{1'})+(h_{2'}-h_{2}))・・・(56)$$

(56)式となります。

したがって、熱効率ηは、

$$η=\frac{W_{t}}{Q_{1}}=\frac{(h_{1}-h_{1'})+(h_{2'}-h_{2})}{(h_{1}-h_{3})+(h_{2'}-h_{1'})}・・・(57)$$

(57)式となります。

冷凍サイクル・ヒートポンプサイクル

冷凍サイクル・ヒートポンプサイクルは外部から仕事を加えることにより熱を移動させるサイクルです。

冷凍機とヒートポンプは基本的に同一の装置・サイクルですが、目的によって呼び方が異なります。

• 冷凍機：低温部から熱を奪うことが目的。
• ヒートポンプ：高温部に熱を供給することが目的。

また、冷凍機とヒートポンプのサイクルはランキンサイクルと全く同じで、サイクルの方向が反対となっています。

そのため、逆ランキンサイクルとも呼ばれます。

逆ランキンサイクルは、圧縮過程の手法によっていくつかの種類に分けられます。

蒸気圧縮冷凍サイクル

圧縮機を使用する冷凍サイクルを蒸気圧縮冷凍サイクルといいます。

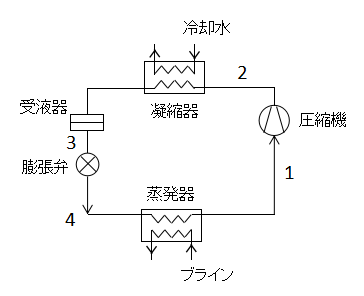
上図に蒸気圧縮冷凍サイクルの構成要素を示します。

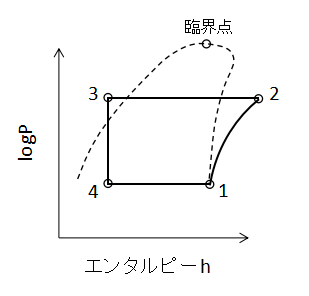
上図に蒸気圧縮冷凍サイクルのPh線図を示します。

冷凍サイクルではTs線図よりはPh線図が出題されることが多いので覚えておきましょう。

1→2(圧縮機での断熱圧縮)

蒸発器で発生した蒸気を断熱圧縮し高温高圧の過熱蒸気にします。この操作は等エントロピー変化となります。

このときの仕事W_c[kW]は、

$$W_{c}=m'(h_{2}-h_{1})・・・(58)$$

m'：質量流量[kg/s]、h₁,h₂：状態1,2での比エンタルピー[kJ/kg]

(58)式で表されます。

2→3(凝縮器での等圧放熱)

凝縮器で過熱蒸気が冷却水に熱を与え、蒸気は液化します。このときの交換熱量Q_c[kW]は、

$$Q_{c}=m'(h_{2}-h_{3})・・・(59)$$

(59)式で表されます。

3→4(膨張弁での絞り膨張)

膨張弁で減圧され、液体が膨張し湿り蒸気となります。

この過程では仕事も熱も加えていませんので、W=Q=0となります。

4→1(蒸発器での蒸発)

蒸発器で冷却媒体から熱を奪って冷却し、サイクル流体は奪った熱によって蒸発します。

このときの交換熱量Q_e[kW]は、

$$Q_{e}=m'(h_{1}-h_{4})・・・(60)$$

(60)式で表されます。

冷凍サイクルでは冷凍機の成績係数ε_rについて問われることが多いです。

$$ε_{r}=\frac{Q_{e}}{W_{c}}=\frac{h_{1}-h_{4}}{h_{2}-h_{1}}・・・(61)$$

成績係数ε_rは(61)式となります。

吸収冷凍サイクル

冷凍サイクルの圧縮過程を冷媒吸収溶液の濃度の違いにより行なうサイクルを吸収冷凍サイクルといいます。

吸収材としては、

• アンモニア(冷媒)-アンモニア水溶液(吸収剤)
• 水(冷媒)-臭化リチウム水溶液(吸収剤)

などが一般的に使用されています。

ただ、試験への出題頻度は低く、ここではサイクルの説明は割愛します。

おわりに

課目Ⅱ"熱と流体の流れの基礎"の出題分野である、熱力学の基礎について解説しました。

課目Ⅱの中では配点が高いため、ぜひとも力を入れて勉強しましょう。