概要
含じんガスを旋回運動させて粒子に遠心力を作用させることで分離する機構を遠心力集塵といい、その代表的な装置をサイクロンといいます。
重力よりも大きい加速度(数百~数千倍)を粒子に与えることができるため、重力集塵よりも小さい粒子を多く捕集することができます。
一般に、分離限界粒子径は3~10μm程度とされていますが、工場で生じる粉じんはこれより小さい粒子も多いです。
したがって、サイクロンは大きめの粒子を捕集する前処理装置として採用されることが多く、小さい粒子は後段に別の装置を設置し除去します。
サイクロン内の流れ
流れの概要
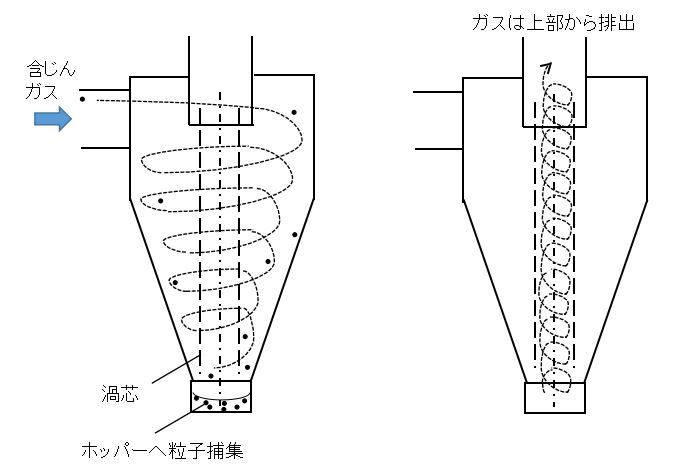
サイクロン内の流れを上図に示します。
通常は外筒上部に入口があり、そこから含じんガスが流入します。
その後、外筒内を旋回しながら下降し、渦芯と呼ばれる中心部に到達します。
ガスは渦芯を旋回しながら上昇し、上部から排出されます。
一方で、粒子は遠心力により壁面に衝突するか、もしくは渦芯で反転上昇する過程で下のホッパーに沈降して分離されます。
このように、外側の下降する旋回流と内側の上昇する旋回流がサイクロン内の流れの特徴です。
渦流れの特徴
また、旋回流(渦流れ)は接線方向のガス流速uθによって渦の特徴が区別されます。
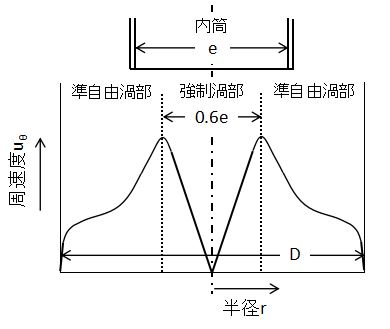
上図にサイクロン内のuθの半径方向分布を示します。
渦芯内でのuθは半径rに比例して大きくなっており、(1)式で表されます。
$$渦芯:u_{θ}=rω・・・(1)$$
ω:角速度[1/s]
(1)式のように角速度ω一定となる渦流れを強制渦といいます。
強制渦部の最も外側でサイクロン内におけるuθの最大値を示し、この距離は内筒直径eの0.6倍程度になることが知られています。
また強制渦部の外側では、半径が大きくなるにつれてuθが小さくなっています。
このときのuθは(2)式で表されます。
$$外環部:u_{θ}r^{n}={\rm{const.}}・・・(2)$$
n:旋回速度指数[-]
n=1となる渦流れを自由渦といいます。
実際のサイクロンではn=0.5~0.9程度の値を取るため、準自由渦または半自由渦といいます。
ちなみに、サイクロンのような強制渦と自由渦が組み合わさった渦をランキン渦といいます。
遠心加速度
粒子は遠心力によってサイクロン内を旋回しながら外側へと移動していきます。
粒子の半径方向へと遠心沈降する速度utcは、遠心力と流体の抗力のつり合いから導かれます。
ストークス則が成り立つとすると、
$$3πμu_{tc}d_{p}=\frac{π}{6}{d_{p}}^{3}(ρ_{P}-ρ)rω^{2}・・・(3)$$
μ:流体粘度[Pa・s]、dp:粒子径[m]、ρp:粒子密度[kg/m3]
ρ:流体密度[kg/m3]、r:半径方向の位置[m]、ω:角速度[1/s]
(3)式となります。(3)式を変形すると、utcは(4)式となります。
$$u_{tc}=\frac{(ρ_{p}-ρ){d_{p}}^{2}}{18μ}rω^{2}=\frac{(ρ_{p}-ρ){d_{p}}^{2}}{18μ}\frac{{u_{θ}}^{2}}{r}・・・(4)$$
uθ:接線方向の流速[m/s]
また、重力沈降速度utは
$$u_{t}=\frac{(ρ_{p}-ρ){d_{p}}^{2}}{18μ}g・・・(5)$$
(5)式となります。
ここで、遠心加速度の重力加速度に対する比をZとすると、(4)、(5)式の比較から、
$$Z=\frac{{u_{θ}}^{2}/r}{g}・・・(6)$$
(6)式となります。
通常、uθ=7~20m/s程度となることから、Zは数百~数千の値となり、重力集塵に比べて大きな加速度が得られることがわかります。
分離限界粒子径
サイクロンの分離限界粒子径は仮定をおいて導出された式がいくつか発表されています。
本記事ではその一部を紹介します。
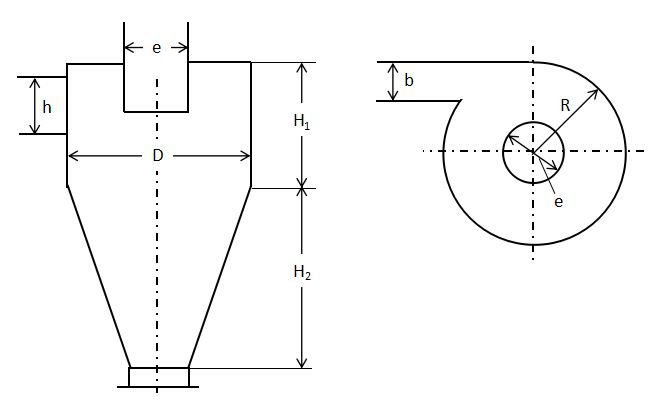
まず、サイクロンの寸法図を以下に示します。
Rosinらの式
簡易式
Rosinらはサイクロン入口から流入した気流が、入口形状(矩形、幅b×高さh)を保ったままN回転して排出されると仮定しました。
この間に粒子は幅bを沈降すると考えます。
このとき、遠心力による沈降速度utcは前述した(4)式となります。
$$u_{tc}=\frac{(ρ_{p}-ρ){d_{p}}^{2}{u_{θ}}^{2}}{18μR}・・・(4)$$
R:サイクロンの半径[m]
次にN回転するのに要する時間t[s]は、
$$t=\frac{2πRN}{u_{θ}}・・・(7)$$
(7)式となります。
粒子の分離が完全に起こるためには(8)式であることが必要です。
$$t≧\frac{b}{u_{tc}}・・・(8)$$
完全に分離される最小粒子では、(8)式の等号が成立します。
$$t=\frac{b}{u_{tc}}・・・(9)$$
(4)、(7)、(9)式から、分離限界粒子径dminは、
$$d_{min}=\sqrt{\frac{9μb}{πNu_{θ}(ρ_{p}-ρ)}}・・・(10)$$
(10)式となります。
遠心沈降速度式による導出
より厳密には遠心沈降速度式を解くことで分離限界粒子径dminが導かれます。
半径rの位置にある直径dpの粒子について、半径方向へと遠心沈降する速度utcは
$$\frac{dr}{dt}=\frac{(ρ_{p}-ρ){d_{p}}^{2}}{18μ}\frac{{u_{θ}}^{2}}{r}・・・(11)$$
(11)式で表されます。
サイクロンの直径をDとし、t=0のときに(D/2)-bの位置にある粒子が壁に到達する時間tまで積分します。
t=0のときr=(D/2)-b、t=tのときr=(D/2)となりますから、
$$\int_{(D/2)-b}^{(D/2)}rdr=\frac{(ρ_{p}-ρ){d_{p}}^{2}{u_{θ}}^{2}}{18μ}\int_{0}^{t}dt・・・(12)$$
$$\frac{(D/2)^{2}}{2}-\frac{[(D/2)-b]^{2}}{2}=\frac{(ρ_{p}-ρ){d_{p}}^{2}{u_{θ}}^{2}t}{18μ}・・・(13)$$
積分すると(13)式となります。
また、時間tの間にN回転しますから、
$$t=\frac{2π(D/2)N}{u_{θ}}=\frac{πDN}{u_{θ}}・・・(14)$$
(14)式となります。
(14)式を(13)式に代入し整理すると、
$$d_{p}=d_{min}=3\sqrt{\frac{μb(D-b)}{πNDu_{θ}(ρ_{p}-ρ)}}・・・(15)$$
分離限界粒子径dminは(15)式となります。
回転数は一般にN=5程度で設計するのがよいと言われていますが、簡易的にNを求める式もあります。
$$N=\frac{2H_{1}+H_{2}}{h}・・・(16)$$
H1:円筒上部の長さ[m]、H2:円錐部の長さ[m]、h:気流入口高さ[m]
池森の式
回転数Nを含まない式として、池森の式があります。
サイクロンから排出される最大粒子径dmaxは、
$$d_{max}=\sqrt{\frac{18μ}{πu_{θ}(ρ_{p}-ρ)}}×\frac{e}{2.26\sqrt{H_{1}+H_{2}}}・・・(17)$$
e:内筒直径[m]
(17)式で表されます。
サイクロンから排出される最大粒子径dmaxは、サイクロンで捕集される最小粒子径dminと同義となります。
圧力損失
サイクロンの圧力損失ΔP[Pa]は、入口ダクトのガスの動圧の何倍となるかで表すことが一般的です。
$$ΔP=F\frac{ρ_{g}{u_{1}}^{2}}{2}・・・(18)$$
F:圧力損失係数[-]、ρg:ガス密度[kg/m3]、u1:入口流速[m/s]
圧力損失係数Fの計算式はいくつかありますが、(19)式が比較的よく使用されます。
$$F=\frac{30bh\sqrt{D}}{e^{2}\sqrt{H_{1}+H_{2}}}・・・(19)$$
ちなみにサイクロンの圧力損失は一般に0.1~0.2kPa程度で設計することが多いです。
まとめ
遠心力集塵装置について解説しました。
サイクロンがどのような原理で粒子を分離するかくらいは知っておきましょう。
