概要
ミストエリミネーターの中でも主要な形式の1つがワイヤーメッシュです。
細いワイヤーを編み込んでメッシュ状のシートとし、このシートを複数重ね合わせてミストの捕集効率を増加させています。
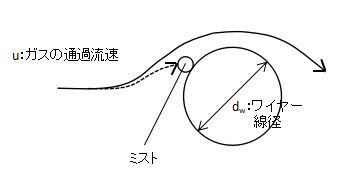
ガスはワイヤーメッシュの網目を通過しますが、ミストは慣性力によりワイヤーに衝突することで捕集されます。
捕集されたミストはいったんワイヤーメッシュに保持され、ガス流速に抗える大きさまで凝集成長すると落下します。
したがってガス流速が速すぎるといったん捕集したミストが再飛散する可能性があり、ワイヤーメッシュの制約条件の1つになります。
主要特性
許容流速
ワイヤーメッシュの許容流速は、Sounders-Brownの関係から(1)式で計算されます。
$$u_{max}=k・\sqrt{\frac{ρ_{L}-ρ_{G}}{ρ_{G}}}・・・(1)$$
umax:最大許容流速[m/s]、k:係数
ρL:ミスト密度[kg/m3]、ρG:ガス密度[kg/m3]
kがワイヤーメッシュの種類に依存する係数で、各メーカーが開示していることがあります。
この(1)式から計算される最大流速は2~3m/s程度となることが多いです。
捕集効率
ワイヤーメッシュによる捕集は慣性衝突機構であるため、粒子半径基準のストークス数Stkに依存します。
$$Stk=\frac{ρ_{L}u{d_{p}}^{2}}{9μd_{w}}・・・(2)$$
ρL:ミスト密度[kg/m3]、u:流速[m/s]、dp:ミスト径[m]
μ:流体粘度{Pa・s]、dw:ワイヤーメッシュの線径[m]
基本的にストークス数が大きい方が、ミストに働く慣性効果が大きくなり捕集されやすくなります。
また、(2)式のストークス数Stkは衝突係数Kとして表されることもあります。
次に、単一繊維捕集効率ηtはストークス数Stkの関数で表されます。
$$η_{t}=f(Stk)・・・(3)$$
ηt:単一繊維捕集効率[-]
(3)式は各メーカーで相関式や相関図が作成されています。
捕集効率ηnは、CarpenterとOthmerが発表した(4)式が使用されることが多いです。
$$η_{n}=1-(1-C・η_{t})^{N}・・・(4)$$
$$C=\frac{2}{3}a_{e}\frac{z}{π}・・・(5)$$
C:係数、N:ワイヤーメッシュの層数[-]
ae:ワイヤーメッシュの比表面積[m2/m3]、z:2層間の距離[m]
係数Cもワイヤーメッシュの種類に依存し、定数で与えられることもあります。
(2)~(5)式から、ワイヤーメッシュの捕集効率を向上させるためには、
- ワイヤーメッシュの線径を細くする
- ワイヤーメッシュの層数を増加する
等が有効であることがわかります。
まとめ
ワイヤーメッシュについてまとめました。
メーカー仕様のバックチェックで計算できる程度に理解しておくとよいでしょう。
