【課目Ⅱ：伝熱工学の基礎】エネルギー管理士(熱分野)の出題分野を解説

概要

この記事ではエネルギー管理士(熱分野)の出題分野である、伝熱工学の基礎について解説します。

伝熱工学の基礎は課目Ⅱ"熱と流体の流れの基礎"の中で、大問4問中1問出題されています。

流体工学の基礎と同様に計算問題が少なく、かつ難易度も比較的簡単です。特に普段実務で扱っている伝熱形態が計算問題として出題されれば確実に点が取れるでしょう。

無次元数

無次元数は頻出で、ほぼ毎年関連する問題が出題されています。

単に無次元数の名前を選択肢から回答する問題や、あるいは対流伝熱等で無次元数を使用した相関式を計算する問題が多いです。

レイノルズ数Re

慣性力と粘性力の比を表わす無次元数です。

$$Re=\frac{ρuL}{μ}=\frac{ud}{ν}・・・(1)$$

ρ：流体密度[kg/m3]、u：代表流速[m/s]、L：代表長さ[m]

μ：流体粘度[Pa・s]、ν：動粘度(動粘性係数)[m²/s]

最も有名な無次元数の1つであるため、名前を答える問題としてはほぼ出題されず、計算問題で出題されることが多いです。

対流伝熱の相関式と合わせて覚えましょう。

 

配管内流れにおいては、代表流速を断面平均流速、代表長さを管内径とします。

以下の記事で別途解説しています。

【レイノルズ数】について解説：流れの無次元数

流れの状態を表わす無次元数をレイノルズ数Reといいます。レイノルズ数の計算を行ない値を知ることで、その流れが層流か乱流かを判別することができます。

続きを見る

ヌセルト数Nu

対流による熱伝達と熱伝導の比を表わす無次元数です。

$$Nu=\frac{hL}{k}・・・(2)$$

h：熱伝達率(境膜伝熱係数)[W/(m²K)]、L：代表長さ[m]

k：流体の熱伝導度[W/(m・K)]

対流伝熱の相関式はヌセルト数、レイノルズ数、プラントル数で表されることが多く、ヌセルト数から対流伝熱の熱伝達率hを算出します。

以下の記事で別途解説しています。

【ヌセルト数】について解説：熱伝達と熱伝導の比

対流熱伝達と熱伝導の比を表わす無次元数をヌセルト数Nuといいます。実用的には、熱伝達率hを算出するのにヌセルト数は使用されます。熱交換器や撹拌槽等の伝熱計算において非常に重要な無次元数です。

続きを見る

プラントル数Pr

速度境界層と温度境界層の厚みの比を表わす無次元数です。

$$Pr=\frac{C_{p}μ}{k}=\frac{ν}{α}・・・(3)$$

C_p：流体の比熱[J/(kg・K)]、μ：流体粘度[Pa・s]、k：流体の熱伝導度[W/(m・K)]

ν：動粘度(動粘性係数)[m²/s]、α：熱拡散係数[m²/s]

流体の物性値のみで表される無次元数であり、流体固有の値となります。

以下の記事で別途解説しています。

【プラントル数】について解説：速度境界層と温度境界層の厚みの比

速度境界層と温度境界層の厚みの比を表わす無次元数をプラントル数Prといいます。プラントル数を表わすパラメータは全て物質に固有な物性値となっており、レイノルズ数やヌセルト数と違って流れに依存しないのが特徴です。

続きを見る

グラスホフ数Gr

浮力と粘性力の比を表わす無次元数です。

$$Gr=\frac{gβΔTL^{3}}{ν^{2}}・・・(4)$$

g：重力加速度[m/s²]、β：体膨張係数[1/K]、ΔT：温度差[K]、L：代表長さ[m]

ν：動粘度(動粘性係数)[m²/s]

自然対流において、流れが層流になるか乱流になるかを示す指標で、Gr=10⁸～10⁹程度で乱流に遷移します。

以下の記事で別途解説しています。

【グラスホフ数】について解説：自然対流における浮力と粘性力の比

浮力と粘性力の比を表わす無次元数をグラスホフ数Grといいます。自然対流においては、流体の温度差によって密度差が生じ、その密度差で生じる浮力が流体の流れの駆動力となります。実用上は、自然対流における熱伝達率hを算出するのにグラスホフ数がGrが使用されます。

続きを見る

レイリー数Ra

浮力と温度拡散率の比を表わす無次元数です。

$$Ra=\frac{gβΔTL^{3}}{να}=Gr・Pr・・・(5)$$

g：重力加速度[m/s²]、β：体膨張係数[1/K]、ΔT：温度差[K]、L：代表長さ[m]

ν：動粘度(動粘性係数)[m²/s]、α：熱拡散係数[m²/s]

グラスホフ数Grとプラントル数Prの積で表されます。

自然対流における熱伝達の形態を表わします。臨界レイリー数以下では熱伝導によって伝熱し、臨界レイリー数以上では対流によって伝熱します。

シュミット数Sc

流体の速度境界層と濃度境界層の厚みの比を表わす無次元数です。

$$Sc=\frac{μ}{ρD}=\frac{ν}{D}・・・(6)$$

μ：流体粘度[Pa・s]、ρ：流体密度[kg/m3]、D：拡散係数[m²/s]

ν：動粘度(動粘性係数)[m²/s]

伝熱におけるプラントル数Prと対応する無次元数です。

以下の記事で別途解説しています。

【シュミット数】について解説：速度境界層と濃度境界層の厚みの比

速度境界層の厚みと濃度境界層の厚みの比を表わす無次元数をシュミット数Scといいます。実用上は、シャーウッド数Shがシュミット数、レイノルズ数の関数となっており、シャーウッド数に含まれる物質移動係数kを算出するのにシュミット数が使用されます。

続きを見る

シャーウッド数Sh

代表長さと境膜の厚みの比を表わす無次元数です。

$$Sh=\frac{h_{D}L}{D}≒\frac{L}{δ}・・・(7)$$

h_D：物質移動係数[m/s]、L：代表長さ[m]、D：拡散係数[m²/s]

伝熱におけるヌセルト数Nuと対応する無次元数です。

以下の記事で別途解説しています。

【シャーウッド数】について解説：対流物質移動と分子拡散の比

対流による物質移動流束と分子拡散による物質移動流束の比を表わす無次元数をシャーウッド数Shといいます。実用上は、シャーウッド数に含まれる物質移動係数kを算出するのに使用することが多いです。

続きを見る

ビオ数Bi

固体内部の熱伝導と固体表面の熱伝導の比を表わす無次元数です。

$$Bi=\frac{hL}{k}・・・(8)$$

h：熱伝達率(境膜伝熱係数)[W/(m²K)]、L：代表長さ[m]

k：固体の熱伝導度[W/(m・K)]

ビオ数が1を超えると固体内部の熱伝導が遅く、固体内部の温度勾配が無視できなくなります。

以下の記事で別途解説しています。

【ビオ数】について解説：固体表面の熱伝達と固体内部の熱伝導の比

固体表面の熱伝達と固体内部の熱伝導の比を表わす無次元数をビオ数Biといいます。ビオ数が小さいと固体表面の熱伝達より固体内部の熱伝導が支配的となり、固体表面から固体内部まで一瞬で熱が伝わります。

続きを見る

伝導伝熱

フーリエの法則

伝導伝熱に関する問題は基本的にフーリエの法則を覚えていれば解けます。

$$q=-k\frac{dT}{dx}・・・(9)$$

q：熱流束[W/m²]、k：熱伝導度[W/(m・K)]

T：温度[K]、x：物質の厚み[m]

フーリエの法則については以下の記事で解説しています。

【フーリエの法則】を解説：伝導伝熱の基本法則

同一物質内、あるいは密接した物体間に温度差がある場合、物質の移動を伴わない熱エネルギーのみの移動現象が発生します。この現象を伝導伝熱といい、伝導伝熱における伝熱量の関係をフーリエの法則といいます。

続きを見る

熱流束q[W/m²]から伝熱量Q[W]を求める場合は、熱が通過する断面積A[m²]をかけましょう。

$$Q=q×A・・・(10)$$

対流伝熱

ニュートンの冷却法則

対流伝熱はニュートンの冷却法則から、

$$q=h(T_{w}-T_{bulk})・・・(11)$$

q：熱流束[W/m²]、h：熱伝達率(境膜伝熱係数)[W/(m²K)]

T_w：壁面温度[K]、T_bulk：流体のバルク温度[K]

(11)式で表されます。

計算問題で出題されることがあるので、覚えておきましょう。

熱伝達率の概略値

熱伝達率の概略値が過去に出題されたことがあります。

熱伝達率hはヌセルト数の相関式などから推算しますが、だいたいどのくらいの値となるのか知っておくのは実務でも非常に重要です。

流体	伝熱形態	熱伝達率 の概略値[W/(m2K)]	備考
水	自然対流	500～550	20℃の水中に50℃の鉛直平板
	強制対流	5,000	内径0.05m、壁温130℃の円管内を40℃の水が1m/sで流れる
	沸騰	約1,500～60,000	0.1MPa、熱流束1MW/m2付近 （バーンアウト付近）
	凝縮	約10,000～230,000
空気	自然対流	5～10	0.1MPa、20℃の空気中に500℃の鉛直平板
	強制対流	40	内径0.05m、壁温130℃の円管内を40℃の空気が10m/sで流れる

伝熱形態として、自然対流がよりも強制対流の方が伝熱が良いことは覚えておきましょう。

熱伝達率の相関式

熱伝達率の相関式を使用してヌセルト数Nuや熱伝達率hを算出する問題が出題されています。

相関式自体は問題文中で与えられることが多く、覚える必要性は低いです。レイノルズ数とプラントル数等の無次元数を覚えておけば計算できます。

コルバーンの式

円管内乱流を計算する場合の代表的な式がコルバーンの式です。

$$Nu=0.023Re^{0.8}Pr^{\frac{1}{3}}・・・(12)$$

試験では関数電卓が使用できないので、代わりに指数表が問題文中に記載されており、値を読み取って計算します。

相変化を伴う熱伝達

沸騰伝熱及び凝縮伝熱に関する語句が問われることがあります。

沸騰伝熱

容器内の静止した液体中に白金線等の熱源を設置し加熱する場合において、加熱面と液の温度差T_w-T_sと熱流束qの関係を下図に示します。

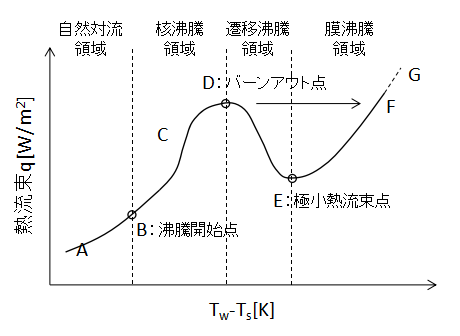
この図のような沸騰を伴う熱伝達の特性を表わしたものを沸騰曲線と呼びます。

 

A-B領域

この領域はまだ沸騰せず自然対流伝熱による顕熱増加が起こっています。

 

B-C-D領域

B点が沸騰開始点で、この点を超えると伝熱表面で沸騰が開始して蒸気の気泡が発生します。

このような個々の気泡が分離して発生する状態を核沸騰といいます。

核沸領域では過熱度を増加させると熱流束は急激に増大し、最終的にD点で極大に達します。

 

D-F-G領域

D点からさらに過熱度を上げると、伝熱面温度が急激に上昇し突然F点に移行します。

一般にF点の温度は非常に高く、金属の融点以上であることが多いので加熱体が融解することが多いです。

そのような理由から、D点をバーンアウト点と呼びます。

F点に移行しても加熱体が融解せず、さらに過熱度を上げることが出来れば、G点へとさらに熱流束が増大していきます。

F点やG点の領域では加熱面の表面を薄くて安定した蒸気の膜が覆い、この膜と液体との気液界面で蒸発が生じるようになります。

この状態を膜沸騰といいます。

 

D-E-F領域

F点やG点に達した後、過熱度を下げると、いきなりD点には戻らずE点に向かいます。

E-F領域では膜沸騰状態が続き、E点で熱流束が極小値となります。

D-E領域は核沸騰と膜沸騰の遷移領域で、大きな気泡が発生したり蒸気の膜が形成されたり不安定な状態となっています。

凝縮伝熱

蒸気が飽和温度以下の冷却面に接触すると、蒸気はその面上で凝縮します。

その際に2つの伝熱形態に分類できます。

 

膜状凝縮

冷却面が濡れやすい場合、凝縮液は冷却面上に膜状に広がって流れ落ちます。

これを膜状凝縮といいます。

 

滴状凝縮

冷却面が濡れにくい場合、凝縮液は冷却面上で膜状に広がらず、表面張力の作用で多数の液滴となります。

液滴は引き続く凝縮で成長したり、合一して大きくなり、ある大きさに達すると流れ落ちます。

これを滴状凝縮といいます。

放射伝熱

放射伝熱はほぼ毎年出題されており、非常に重要です。

ただし、語句を問う問題から計算問題まで出題形式は様々で広く勉強する必要があります。

吸収率・反射率・透過率

物体に熱放射線が当たると、その一部は吸収され、一部は反射され、残りは透過します。この関係を式で表すと、

$$α+ρ+τ=1・・・(13)$$

α：吸収率、ρ：反射率、τ：透過率

(13)式となります。

黒体

熱放射を考えるうえでの理想的な物質として、反射率ρ=透過率τ=0、吸収率α=1となるものを黒体といいます。

黒体に到達した熱放射線は全波長にわたって完全に吸収されます。

プランクの法則

黒体の単色放射能に関する法則をプランクの法則といいます。

$$E_{bλ}=\frac{C_{1}}{λ^{5}({\rm{exp}}(\frac{C_{2}}{λT})-1)}・・・(14)$$

E_bλ：微小波長範囲当たりの放射能[(W/m²)/m]、λ：波長[m]

C₁=3.74×10^-16[W・m⁴/m²]

C₂=1.44×10^-2[m・K]

(14)式そのものを使って計算することはあまりないと思いますが、法則の名前くらいは覚えておきましょう。

ウィーンの変位則

温度の上昇につれて、単色放射能の極大値を与える波長が短くなっていく性質をウィーンの変位則といいます。

これもとりあえず語句だけ覚えておきましょう。

ステファン・ボルツマンの法則

黒体の全放射能に関する法則をステファン・ボルツマンの法則といいます。

(14)式を全波長にわたって積分することで(15)式が得られます。細かい導出は割愛します。

$$E_{b}=σT^{4}・・・(15)$$

T：温度[K]、σ：ステファン・ボルツマン定数(5.67×10^-8)[W/(m²K⁴)]

放射伝熱の計算では(15)式を使用する問題が最も多いでしょう。

灰色体

通常の物質は、波長によって放射能が変化するため複雑です。

そこで、理論的な取り扱いを簡単にするために、灰色体という概念が導入されました。

灰色体の放射能は黒体放射を基準として、物体からの放射能をその物体と同じ温度の黒体の放射能に対する割合εで表しています。

式で表すと、

$$E=εσT^{4}・・・(16)$$

ε：(全)放射率[-]

(16)式となります。

放射率εの値は、波長や温度によらず一定と定義されています。

キルヒホッフの法則

どのような物質でも、その単色放射率と単色吸収率は同じ値であるとする法則をキルヒホッフの法則といいます。

$$ε=α・・・(17)$$

式で書くと(17)式となります。

黒体表面間の放射伝熱

黒体1から黒体2への放射伝熱量Q₁₂[W]は、

$$Q_{12}=σ({T_{1}}^{4}-{T_{2}}^{4})A_{1}F_{12}=σ({T_{1}}^{4}-{T_{2}}^{4})A_{2}F_{21}・・・(18)$$

σ：ステファン・ボルツマン定数[W/(m²K⁴)]

T₁：黒体1の表面温度[K]、T₂：黒体2の表面温度[K]

A₁：黒体1の表面積[m²]、A₂：黒体2の表面積[m²]

F₁₂：A1面を基準にしてA2面を見た場合の形態係数[-]

F₂₁：A2面を基準にしてA1面を見た場合の形態係数[-]

(18)式で表されます。

過去には式の形や計算問題として出題されたことがありますので覚えておきましょう。

灰色体表面間の放射伝熱

灰色体は黒体と違って放射エネルギーを全て吸収せず、一部を反射しますから計算は複雑化します。

式の導出から理解しておいた方がよいでしょう。

灰色体1、灰色体2の間のみの放射伝熱を考えます。

 

まず、灰色体1から発するエネルギーQ₁'は、灰色体1自身から放射されるエネルギーと、灰色体2から灰色体1に入射するエネルギーにうち反射するものとの和で表されるので、

$$Q_{1}'=ε_{1}σ{T_{1}}^{4}A_{1}+ρ_{1}Q_{2}'F_{21}・・・(19)$$

ε₁：灰色体1の放射率[-]、ρ₁：灰色体2の反射率[-]

Q₁'：灰色体1から発するエネルギー[W]、Q₂'：灰色体2から発するエネルギー[W]

(19)式となります。

次に灰色体1から発するエネルギーQ₂'は同様に、

$$Q_{2}'=ε_{2}σ{T_{2}}^{4}A_{2}+ρ_{2}Q_{2}''・・・(20)$$

Q₂''：灰色体2に入射するエネルギー[W]

(20)式で表されます。

 

放射伝熱は灰色体1,2の間のみで行われ、外界に散逸しないため、灰色体1が失うエネルギーと灰色体2が得るエネルギーは等しくなります。

したがって、灰色体1から2への放射伝熱量Q₁₂は、

$$Q_{12}=Q_{1}'-Q_{1}''=Q_{2}''-Q_{1}'・・・(21)$$

Q₁'：灰色体1から発するエネルギー[W]、Q₂'：灰色体2から発するエネルギー[W]

Q₁''：灰色体1に入射するエネルギー[W]、Q₂''：灰色体2に入射するエネルギー[W]

(21)式となります。

また、Q'とQ''は、

$$Q_{1}''=Q_{2}'F_{21}・・・(22)$$

$$Q_{2}''=Q_{1}'F_{12}・・・(23)$$

(22)、(23)式の関係が成り立ちます。

ここで、(21)式に(19)、(22)式を代入すると、

$$Q_{12}=ε_{1}σ{T_{1}}^{4}A_{1}+ρ_{1}Q_{2}'F_{21}-Q_{2}'F_{21}$$

(13)式について透過率τ=0なので、ε₁=1-ρ₁となり、

$$Q_{12}=ε_{1}σ{T_{1}}^{4}A_{1}-ε_{1}Q_{2}'F_{21}・・・(24)$$

(24)式となります。

続いてQ₂'について、(20)式に(21)式、(24)式を代入し、

$$\begin{align}Q_{2}'&=ε_{2}σ{T_{2}}^{4}A_{2}+ρ_{2}(Q_{1}'-Q_{1}''+Q_{2}')\\&=ε_{2}σ{T_{2}}^{4}A_{2}+ρ_{2}(ε_{1}σ{T_{1}}^{4}A_{1}-ε_{1}Q_{2}'F_{21}+Q_{2}')\end{align}$$

ε₂=1-ρ₂の関係を使用しつつ、Q2'=の形に変形すると、

$$Q_{2}'=\frac{ε_{2}σ{T_{2}}^{4}A_{2}+ε_{1}ρ_{2}σ{T_{1}}^{4}A_{1}}{ε_{2}+ρ_{2}ε_{1}F_{21}}・・・(25)$$

(25)式となります。

あとは(25)式を(24)式に代入してε₂=1-ρ₂の関係を使用しつつ整理します。

$$\begin{align}Q_{12}&=ε_{1}σ{T_{1}}^{4}A_{1}-ε_{1}F_{21}・\frac{ε_{2}σ{T_{2}}^{4}A_{2}+ε_{1}ρ_{2}σ{T_{1}}^{4}A_{1}}{ε_{2}+ρ_{2}ε_{1}F_{21}}\\&=\frac{ε_{1}ε_{2}σ{T_{1}}^{4}A_{1}-ε_{1}ε_{2}σ{T_{2}}^{4}A_{2}F_{21}}{ε_{2}+ρ_{2}ε_{1}F_{21}}\\&=\frac{σ({T_{1}}^{4}A_{1}-{T_{2}}^{4}A_{2}F_{21})}{\frac{1}{ε_{1}}+(\frac{1}{ε_{2}}-1)F_{21}}・・・(26)\end{align}$$

(26)式となります。

(26)式の両辺をA₁で割ると、

$$\frac{Q_{12}}{A_{1}}=\frac{σ({T_{1}}^{4}-{T_{2}}^{4}\frac{A_{2}}{A_{1}}F_{21})}{\frac{1}{ε_{1}}+(\frac{1}{ε_{2}}-1)F_{21}}・・・(27)$$

(27)式となります。

(27)式が最終的な灰色体間の放射伝熱式となりますが、形態係数Fの値次第では簡略化できます。

 

十分に広く面積の等しい平行平面の場合

$$F_{12}=F_{21}=1・・・(28)$$

$$A_{1}=A_{2}・・・(29)$$

(28)、(29)式から(27)式は

$$\frac{Q_{12}}{A_{1}}=\frac{σ({T_{1}}^{4}-{T_{2}}^{4})}{\frac{1}{ε_{1}}+(\frac{1}{ε_{2}}-1)}・・・(30)$$

(30)式に簡略化できます。

 

凹部のない灰色体表面1が表面2に完全に囲まれている場合

$$F_{21}=\frac{A_{1}}{A_{2}}・・・(31)$$

(31)式から(27)式は

$$\frac{Q_{12}}{A_{1}}=\frac{σ({T_{1}}^{4}-{T_{2}}^{4})}{\frac{1}{ε_{1}}+(\frac{1}{ε_{2}}-1)\frac{A_{1}}{A_{2}}}・・・(32)$$

(32)式に簡略化できます。

熱交換

試験では熱交換器の伝熱計算について出題されることが多いです。

熱交換器では、伝導伝熱と対流伝熱が複合した伝熱形態となっており、これまでの分野の応用的な位置付けです。

熱通過抵抗・熱通過率

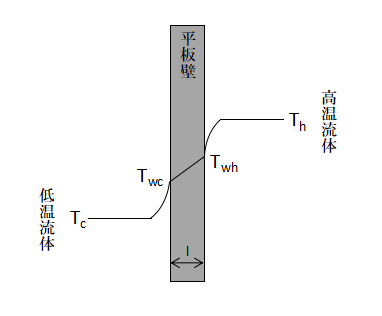
上図のように平板を通じて高温流体から低温流体へと伝熱する系について考えます。

流体が流れている領域ではニュートンの冷却法則、平板ではフーリエの法則が成り立つことから、

$$Q=h_{1}A(T_{h}-T_{wh})・・・(33)$$

$$Q=\frac{kA}{l}(T_{wh}-T_{wc})・・・(34)$$

$$Q=h_{2}A(T_{wc}-T_{c})・・・(35)$$

(33)～(35)式が成り立ちます。

3つの式について、辺々足し合わせて整理すると、

$$Q=\frac{T_{h}-T_{c}}{R}・・・(36)$$

$$R=\frac{1}{h_{1}A}+\frac{l}{kA}+\frac{1}{h_{1}A}・・・(37)$$

(36)、(37)式となります。

Rを熱通過抵抗といいます。

また、(36)、(37)式は、

$$Q=KA(T_{h}-T_{c})・・・(38)$$

$$K=\frac{1}{RA}=\frac{1}{\frac{1}{h_{1}}+\frac{l}{k}+\frac{1}{h_{1}}}・・・(39)$$

(38)、(39)式の形でも表すことができます。

Kを熱通過率といいます。私の職場ではKを総括伝熱係数Uと呼ぶことが多いです。

熱交換器の種類

熱交換器の種類に関しては、以下の記事で解説しています。

【熱交換器】を目的や構造ごとに解説：プラントの重要な伝熱装置

温度の異なる流体を流し、熱交換させる装置のことを熱交換器といいます。
化学プラントではそれぞれの工程や装置ごとに様々な温度で運転しているため、所定の温度まで加熱、あるいは冷却する装置が必須です。

続きを見る

 

また、流体の流れる向きによって、並流形、向流形、直交流形、多重パス形などに分類されます。

特に試験で出題されやすいのが並流形と向流形です。

向流形の方が流体の温度差を大きく取れるので、並流形の熱交換器よりもよく使用されます。

対数平均温度差

対数平均温度差を算出する式の形を問われたことがあります。

以下の記事で解説しています。

【対数平均温度差(LMTD)】を解説：熱交換器の代表温度差

交換熱量の計算にあたって温度差を求める必要がありますが、入口と出口で温度が異なる場合はどの区間で温度差を取るべきか判断が難しいです。そこで高温流体、低温流体の入口、出口の温度からその装置の温度差を代表的に計算した値を交換熱量の計算に使用します。この温度差のことを対数平均温度差ΔTlmといいます。

続きを見る

 

また、対数平均温度差と比較されるような形で、算術平均温度差が出題されることがあります。

$$ΔT_{av}=\frac{ΔT_{1}+ΔT_{2}}{2}・・・(40)$$

$$ΔT_{1}=T_{h1}-T_{c1}・・・(41)$$

$$ΔT_{1}=T_{h2}-T_{c2}・・・(42)$$

T_h1：高温側流体の入口温度[K]、T_h2：高温側流体の出口温度[K]

T_c1：低温側流体の出口温度[K]、T_c2：低温側流体の入口温度[K]

熱交換器の各々の入口側、出口側の流体の温度差がそれほど変わらない場合には、算術平均としても差し支えないとされています。

ただ、正直実務で算術平均温度差を使う必要性を感じないので、対数平均温度差をちゃんと覚えた方がよいでしょう。

温度効率

熱交換器の性能を評価する指標の1つです。

温度効率ηとは、熱交換器における高温・低温流体の温度差の最大値に対して、実際に高温流体の温度がどのくらい減少したか、あるいは低温流体の温度がどのくらい増加したかを表わしています。

$$η_{h}=\frac{T_{h,in}-T_{h,out}}{T_{h,in}-T_{c,in}}・・・(43)$$

$$η_{c}=\frac{T_{c,out}-T_{c,in}}{T_{h,in}-T_{c,in}}・・・(44)$$

高温流体の温度効率η_h、低温流体の温度効率η_cは(43)、(44)式で表されます。

エネルギー効率

同様に熱交換器の性能を評価する指標の1つです。

エネルギー効率εとは、熱力学的に達成可能な最大交換熱量に対して、実際にどのくらい熱交換したかを表わしています。

$$ε=\frac{C_{h}(T_{h,in}-T_{h,out})}{C_{min}(T_{h,in}-T_{c,in})}=\frac{C_{c}(T_{c,out}-T_{c,in})}{C_{min}(T_{h,in}-T_{c,in})}・・・(45)$$

$$C_{h}=m_{h}C_{ph}・・・(46)$$

$$C_{c}=m_{c}C_{pc}・・・(47)$$

C_h：高温流体の熱容量[W/K]、C_c：低温流体の熱容量[W/K]

C_min：高温流体、低温流体の熱容量のうち、小さい方の熱容量[W/K]

m_h：高温流体の質量流量[kg/s]、m_c：低温流体の質量流量[kg/s]

C_ph：高温流体の定圧比熱[J/(kg・K)]、C_pc：低温流体の定圧比熱[J/(kg・K)]

エネルギー効率εは(45)式で表されます。

また、関連して、熱容量の大きい方と小さい方の比を水当量比Λといいます。

$$Λ=\frac{C_{min}}{C_{max}}・・・(48)$$

伝熱単位数(NTU)

同様に熱交換器の性能を評価する指標の1つです。

伝熱単位数(Number of Heat Transfer Unit)は熱交換器の特性を評価するための無次元数です。

$$NTU=\frac{KA}{C_{min}}・・・(49)$$

K：熱通過率[W/(m²K)]、A：伝熱面積[m2]

C_min：高温流体、低温流体の熱容量のうち、小さい方の熱容量[W/K]

NTUはエネルギー効率εとの関係式で主に使用されます。導出は省きますが、

並流形の場合

$$ε=\frac{1-{\rm{exp}}(-(1+Λ)・NTU)}{1+Λ}・・・(50)$$

向流形の場合

$$ε=\frac{1-{\rm{exp}}(-(1-Λ)・NTU)}{1-Λ{\rm{exp}}(-(1-Λ)・NTU)}・・・(51)$$

並流形、向流形の関係式は(50)、(51)式となります。

これらの式をもとに、縦軸にε、横軸にNTUをプロットしたものをε-NTU線図といいます。

熱交換器の参考書には様々な型式についてのε-NTU線図が記載されており、熱交換器の設計に役立ちます。

おわりに

課目Ⅱの伝熱工学の基礎について解説しました。

公式の丸暗記だと対応できないこともあるので、導出から理解しておいた方がよいでしょう。