概要
蒸留塔の塔頂から流出した蒸気を凝縮させて液にし、塔内へ戻す操作のことを還流といいます。
精留塔においては還流をすることが必須条件になっています。
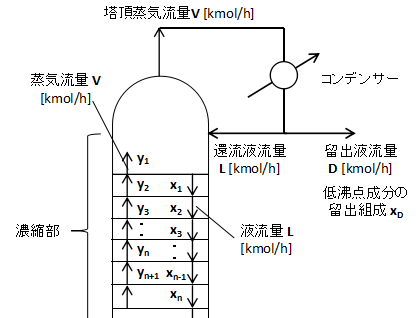
上図に塔頂付近の液とガスの流れを示します。
精留塔では各段で気液接触することで低沸点成分が濃縮されて塔頂に集まります。
もし還流をしなければ、原料供給段から蒸発するガスは液と接触せずにそのまま塔頂まで上がってしまいます。
このような状態はいわゆるフラッシュ蒸留と同じで、気液平衡1回分の濃縮効果しかありません。
そのため塔頂蒸気を冷却し液として戻すことで気液平衡の回数を稼ぎ濃縮効果を高めている、というわけです。
また、塔頂に戻す液はなんでもよいというわけではありません。
塔頂蒸気に近い組成の液を戻すのが低沸点成分の濃縮効率が良いです。
低沸点成分の組成が少ない液を塔頂に戻してしまうと、せっかく濃縮した低沸点成分の純度が悪くなってしまいます。
逆に最も濃縮効果が高い還流液は低沸点成分の純度100%の液です。
しかし低沸点成分の純度を上げたくてやっている蒸留で、純度100%の液をわざわざ塔へ戻すのはナンセンスです。
したがって、塔頂から出るガスを冷やして塔へ戻すのが最も経済的だということになります。
還流比
塔頂から抜き出す量に対して、どのくらいの割合で塔内に戻すのかは塔の設計、運転上で非常に重要です。
この割合のことを還流比といいます。
還流比に関しては様々な用語がありますので、ざっと紹介します。
外部還流比
塔頂蒸気を凝縮後に、液として系外へ抜き出す量をD、塔内へ還流する量をLとすると
$$外部還流比R=\frac{L}{D}$$
外部還流比Rは上式で表されます。
一般に還流比と言えば、この外部還流比を指します。
外部還流比は0~∞の範囲で変化します。
R=0だと還流をかけず、全て抜き出す状態を表わします。
R=∞は塔頂から液を全く抜き出さず(D=0)、全ての凝縮液を塔内に戻すことを意味します。
この状態を特に全還流と呼びます。
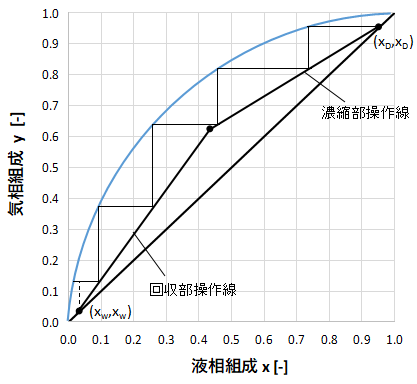
上図にはxy線図を示します。
2成分の気液平衡曲線及び、McCabe-Thiele法より濃縮部操作線、回収部操作線及び階段作図をしています。
通常の蒸留塔の運転では上図のように濃縮部操作線と回収部操作線が、気液平衡曲線とy=xの間を通っています。
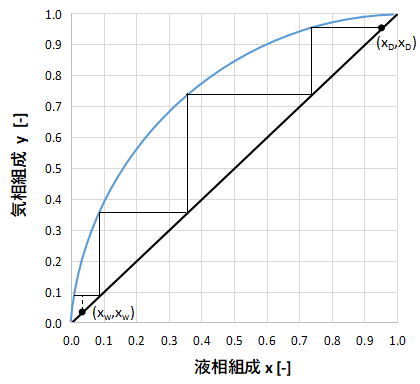
一方で、全還流の状態になると2つの操作線の傾きがy=xと一致し、上図のようになります。
全還流の状態で階段作図すると、最も階段の段数が小さくなりますね。
したがって全還流の状態は、理論上最も塔の濃縮効果が高くなります。
ただし塔から液を抜き出さないため、連続式精留塔では全還流で運転することはできません。
しかし、回分式精留塔の場合は全還流運転で一時的に塔の濃縮効果を高める運転をすることがあります。
また、連続式精留塔の場合でも運転立ち上げ時には、塔内温度が安定するまで全還流運転をすることもあります。
内部還流比
精留塔のある断面において、流下する液量をL、上昇するガス流量をVとすると
$$内部還流比r=\frac{L}{V}$$
内部還流比rは上式で表されます。
一般には外部還流比を制御して液ガス比を決めることが多く、内部還流比はあまり意識されません。
ただ、塔内で部分的に内部還流比が大きすぎたり小さすぎる場合は注意しましょう。
濃縮部と回収部で塔径やインターナルを変えたり、液のフィード段が適切でないと内部還流比に大きな差が出る可能性があります。
最小還流比
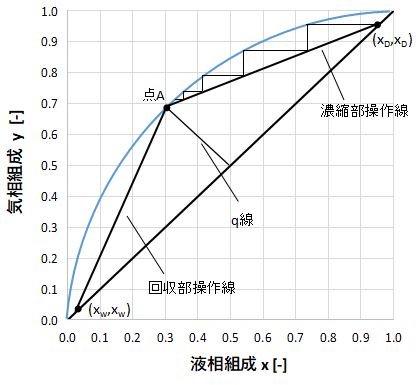
上図にxy線図を示します。
同様に2成分の気液平衡曲線及び、McCabe-Thiele法より濃縮部操作線、回収部操作線及び階段作図をしています。
濃縮部操作線と回収部操作線の交わる点はq線上にあり、塔の運転条件によって変化します。
上図のように気液平衡曲線と濃縮部操作線、回収部操作線が交わった場合の還流比を特に最小還流比Rmといいます。
最小還流の状態となると、点Aを超えて濃縮部から回収部へ蒸留操作をすることができなくなり、理論上は無限の段数が必要になります。
したがって、最小還流比で蒸留塔の運転をすることはできません。
しかし蒸留塔の運転還流比を決定するうえで目安になるため重要な指標となります。
おおよそ、最小還流比Rmの1.2~2.0倍で運転還流比が決定されます。
最小還流比の計算方法
2成分でラウールの法則に従う理想溶液系の場合、最小還流比を比較的簡便に計算できる式があります。
原料の熱的状態を表わすq値で場合分けされ、
q=1のとき
$$R_{m}=\frac{1}{α-1}(\frac{x_{D}}{x_{F}}-α\frac{1-x_{D}}{1-x_{F}})$$
q=0のとき
$$R_{m}=\frac{1}{α-1}(\frac{x_{D}}{x_{F}}-\frac{1-x_{D}}{1-x_{F}})-1$$
Rm:最小還流比、α:相対揮発度
xD:低沸分の留出組成、xF:低沸分のフィード組成
でそれぞれ計算できます。
