撹拌槽の伝熱は
・槽壁を覆っているジャケットで熱交換させる
・槽内部に設置したコイルで熱交換させる
・プロセス液を外部循環させる
大まかに上の三種類に分かれます。
この記事ではジャケットでの境膜伝熱係数についてまとめています。
概要
撹拌槽内の流動は撹拌翼のフローパターンによって変化するため、槽壁の境膜伝熱係数もそれに応じて変化します。
撹拌槽内の厳密な流れはナビエ・ストークスの式という偏微分方程式を解かなければ知ることはできません。
したがって境膜伝熱係数も厳密に求めようとすると複雑な式を解かなければなりません。
撹拌槽の設計のたびにそのようなことをするのは非常に時間がかかるため、先人達は境膜伝熱係数を比較的簡単な相関式で求められるよう研究してきました。
その結果、汎用的な撹拌翼に関してはいくつかの相関式が発表されています。
以下ではその相関式について紹介します。
無次元数による相関式
境膜伝熱係数の相関式で知名度が高いのはヌセルト数Nu、レイノルズ数Re、プラントル数Prの相関式でしょう。
$$Nu=\frac{h_{j}D}{λ}=KRe^{a}Pr^{b}(\frac{μ}{μ_{w}})^{c}$$
Nu:ヌセルト数[-]、Re:撹拌レイノルズ数[-]、Pr:プラントル数[-]
hj:槽壁の境膜伝熱係数[W/(m2 K)]、D:槽直径[m]、λ:流体の熱伝導率[J/(m s K)]
K,a,b,c:定数
K,a,b,cは撹拌翼の種類や寸法などの撹拌条件によって変化します。
※文献によって同じ撹拌翼の相関式でも定数が異なる場合がありますので、よく確認することを推奨します。
※また、撹拌条件に関して細かく適用範囲が指定されていることがあります。これについてもよく確認し、外挿となってしまう場合はある程度安全率を多めにとることを心掛けましょう。
| 適用範囲 | K | a | b | c | |
| ①パドル翼、傾斜パドル翼、タービン翼 | 乱流 バッフル有り | 以下参照 | 2/3 | 1/3 | 0.14 |
| ②パドル翼、傾斜パドル翼、タービン翼 | 乱流 バッフル無し | 以下参照 | 2/3 | 1/3 | 0.14 |
| ③プロペラ翼 | 乱流 バッフル有り | 以下参照 | 2/3 | 1/3 | 0.14 |
| ④アンカー翼 | 乱流 | 以下参照 | 2/3 | 1/3 | 0.14 |
| ⑤ヘリカルリボン翼 | 10<Re<1000 Re<0.1 | K=0.45 以下参照 | 0.6 0.17 | 1/3 1/3 | 1/5 1/5 |
定数Kについては各翼で様々な形をとるため、以下に示します。
①パドル翼、傾斜パドル翼、タービン翼(バッフル有り)
$$K=1.40×(\frac{Σbi}{D})^{0.45}(\frac{d}{D})^{-0.3}n_{p}^{0.2}(\frac{ΣCi}{iH})^{0.2}(sinθ)^{0.5}(\frac{H}{D})^{-0.6}$$
d:翼直径[m]、D:槽直径[m]、i:撹拌翼段数[-]、bi:i段目撹拌翼の翼幅[-]、np:翼枚数[-]
H:液高さ[m]、Ci:i段目撹拌翼の槽底部からの高さ[m]、θ:翼角度[rad.]
"熱計算ハンドブック, 日本能率協会,(1988)"を参照
多段翼に対応できるよう撹拌翼の段数がiで与えられています。
②パドル翼、傾斜パドル翼、タービン翼(バッフル無し)
$$K=0.54×(\frac{Σbi}{D})^{0.15}(\frac{d}{D})^{-0.25}n_{p}^{0.15}(\frac{ΣCi}{iH})^{0.15}(sinθ)^{0.5}$$
"熱計算ハンドブック, 日本能率協会,(1988)"を参照
ベースはバッフル有りと同じ式ですが、ところどころ定数が変わっています。
③プロペラ翼
$$K=0.505×{\rm{exp}}(0.3{\rm{ln}}(Z)-0.0144 Z)\\
×[\frac{0.278 {\rm{exp}}[0.0469 {\rm{exp}}(0.923 {\rm{ln}}(Z))]}{(\frac{S}{d_{R}})}+1]^{-1}$$
Z:プロペラ羽根枚数[-]、S/dR:プロペラピッチ比[-]
"熱計算ハンドブック, 日本能率協会,(1988)"を参照
④アンカー翼
$$K=0.46×(\frac{d}{D})^{-0.1}n_{p}^{0.15}(\frac{b sinθ}{H})^{0.15}[1-0.211(0.63-\frac{bn_{p} sinθ}{H})]$$
"ニュートン流体の撹拌槽壁側伝熱係数に関する実験的研究, 水科ら,(1966)"を参照
この式はパドル翼の算出にも兼用できる式のようで、角度θの項が入っています。
アンカー翼の場合はθ=90°とします。
⑤ヘリカルリボン翼
Re<0.1のとき
$$K=[n_{p}/(p/d)(c/d)^{2}]^{0.22}/6$$
np:リボンの羽根枚数[-]、p:翼ピッチ[-]、d:翼直径[m]、c:翼と槽のクリアランス[m]
"撹拌技術, 佐竹化学機械工業,(1992)"を参照
Pvによる相関式
個人的にオススメしたいのがこちらのPvによる相関式です。
$$\frac{h_{j}}{ρC_{p}}=0.13×(\frac{P_{V}μ}{ρ^{2}})^{\frac{1}{4}}Pr^{-\frac{2}{3}}(\frac{μ}{μ_{w}})^{0.14}$$
ρ:液密度[kg/m3]、Cp:液比熱[J/(kg K)]、PV:単位液量当たりの所要動力[kW/m3]
"撹拌技術, 佐竹化学機械工業,(1992)"を参照
この式の意味するところは撹拌翼の種類や寸法が違っても、Pvが同じであれば境膜伝熱係数は同じになるということです。
もちろんフローパターンが違えば局所的な境膜伝熱係数は異なると思いますが、槽全体で平均すると結局同じくらいの伝熱性能になるだろう、ということです。
この式のメリットはPvさえわかれば境膜伝熱係数が計算できるという点です。
無次元数の相関式は撹拌翼の種類や寸法によって式を使い分けする必要があり、式の適用範囲も細かく決まっていることが多いです。
計算したい撹拌槽に限って適用範囲から外れている、ということがありがちなのでPvによる相関式は使い勝手が良いです。
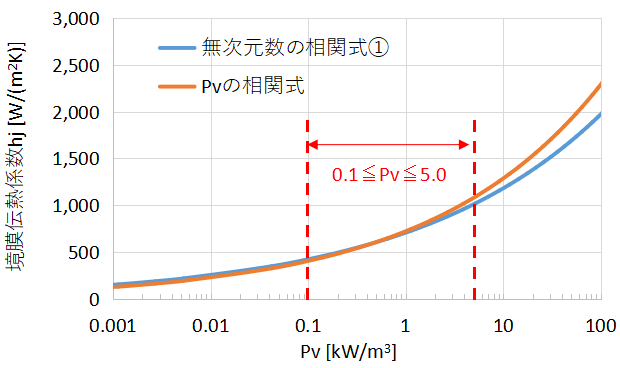
上に同条件で二つの相関式を計算して比較したグラフを示します。
槽径2.0m、翼径1.0m、6枚タービン翼1段の撹拌槽を計算例として使用しました。
結果としてどちらの相関式でも境膜伝熱係数が非常に近い値となり、Pvの相関式でも十分に伝熱能力を推算できることがわかりました。
Pv=10以上ではずれが大きくなりますが、Pv値の記事で述べたように現実的なPv値は0.1~5.0の間であることが多いのでそれほど問題にはなりません。
一方、注意点としてPvの相関式はなるべく乱流領域で使用するのが良いです。
そもそも層流の場合にはアンカー翼やヘリカルリボン翼、メーカー特有の大型翼などの少し特殊な翼を使うことが多いので、その場合にはその翼の相関式を使用するのが良いでしょう。
メーカー特有の翼の場合は相関式がわからないと思いますので、必要があればメーカーに計算を依頼しましょう。
関連記事
攪拌槽の伝熱能力改善手法を解説しました。
-

【撹拌槽伝熱】総括伝熱係数U・伝熱面積A・温度差ΔTそれぞれの改善手法を徹底解説
この記事では撹拌槽の伝熱能力についての考え方や計算方法、どのようにすれば伝熱性能を改善させることができるのか、について解説しています。
続きを見る

