概要
Wegstein法は非線形方程式を解く手法の1つです。Direct法(逐次代入法)をベースとして定数qで補正することで収束性を改善しています。
化学工学計算シミュレータでよく使用される収束計算手法ですので、ぜひ覚えておきましょう。
原理
方程式f(x)=0の解を求めることを考えます。
Direct法ではf(x)=0を変形して、
$$x=g(x)・・・(1)$$
(1)式の形とし、y=xとy=g(x)の交点を算出していました。
Wegstein法では(1)式の右辺を、
$$右辺=qx+(1-q)g(x)$$
q:定数
と変形し、y=xとy=qx+(1-q)g(x)の交点を計算します。
文献等では次のステップのxの値は、
$$x_{k+1}=qx_{k}+(1-q)g(x_{k})・・・(2)$$
(2)式のような形で記述されることが多いです。
qはacceleration parameterと呼ばれる定数で、関数g(x)の形次第で取る値が変化します。
定数qの物理的意味は収束仮定を図で示すとわかりやすいです。
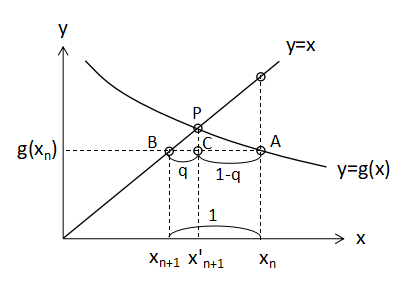
まず、Direct法で任意の値xnをxn+1へ更新する場合は点Aから点Bに移ります。
ここでy=xとy=g(x)との交点をPとし、点Pから線分ABに下した垂線と線分ABとの交点をCとします。
点Cのx座標がWegstein法で更新する値x'n+1とすると、
$$x'_{n+1}=x_{n+1}+\frac{BC}{BA}(x_{n}-x_{n+1})・・・(3)$$
(3)式で表せます。
このときの線分BCの長さをq、線分BAの長さを1とすると、
$$x'_{n+1}=x_{n+1}+q(x_{n}-x_{n+1})・・・(4)$$
(4)式となります。
あとはxn+1=g(xn)なので、
$$x'_{n+1}=g(x_{n})+q(x_{n}-g(x_{n}))=qx_{n}+(1-q)g(x_{n})・・・(2)$$
となり(2)式となります。
したがって、定数qとはxの値を更新するときにDirect法に対してWegstein法がどの程度の比率でx座標を更新するかを表わしているパラメータだと言えます。
また、導出は省きますがqに関しては
$$q=\frac{s}{s-1}・・・(5)$$
$$s=g'(x)≒\frac{g(x_{n})-g(x_{n-1})}{x_{n}-x_{n-1}}・・・(6)$$
(5),(6)式から算出することができます。sは関数g(x)の微分値を示しています。
初期値x0からスタートする場合、x1の値はDirect法で求め、x2の値から定数qを求めWegstein法を使用することができます。
また、算出される定数qの値によって収束計算の傾向が場合分けされており、以下に示します。
q<0のとき
q<0の場合、0<g'(x)<1となります。
Direct法でも容易に収束するケースです。
しかし収束するのに繰り返し計算回数が多くなる場合があります。この場合、Wegstein法ではqをマイナスの値とすることでより交点に近づけることができます。
0<q<1のとき
0<q<1の場合、g'(x)<0となります。
このときは解が振動しがちであることで知られており、うまく初期値を選ぶことで収束させることができます。
q>1のとき
q>1の場合、g'(x)>1となります。
この場合はDirect法では収束しないことで知られており、qを1より大きい値とすることでWegstein法で収束させることができます。
q=0のとき
q=0のとき(2)式から、
$$x_{k+1}=g(x_{k})$$
となりDirect法と一致します。
q=1のとき
q=1のとき(2)式から、
$$x_{k+1}=x_{k}$$
となり前のステップのxの値がそのまま次のステップに使用され、値が更新されません。
なので、あえてq=1で計算する意味はありません。
まとめ
非線形方程式を解く手法の1つであるWegstein法について解説しました。
大学ではあまり習わない割に実務レベルでよく使用される手法です。収束計算をよく行なう場合はよく理解しておきましょう。
