概要
この記事では配管や熱交換器の伝熱管内を流れる流体の境膜伝熱係数についてまとめています。
配管内の流動は他の流れに比べると単純で、種々の相関式が発表されています。
各相関式
コルバーンの実験式
私が学生のころ、授業で習った式で非常にシンプルです。
$$Nu=\frac{h_{i}D}{λ}=0.023Re^{0.8}Pr^{0.4}$$
適用範囲
$$10,000≦Re≦120,000$$
$$0.7≦Pr≦120$$
$$\frac{L}{D}≧60$$
Nu:ヌセルト数[-]、hi:管内側境膜伝熱係数[W/(m2K)]、D:管内径[m]、
λ:流体の熱伝導度[W/mK]、Re:レイノルズ数[-]、Pr:プラントル数[-]
"化学工学便覧改訂六版, 化学工学会,(1999)"を参照
シンプルであるがゆえに適用範囲が少し狭いです。
Siederの式
$$Nu=\frac{h_{i}D}{λ}=j_{H}Pr^{\frac{1}{3}}(\frac{μ}{μ_{w}})^{0.14}$$
適用範囲
$$Pr≧0.7$$
Nu:ヌセルト数[-]、hi:管内側境膜伝熱係数[W/(m2K)]、D:管内径[m]、
λ:流体の熱伝導度[W/mK]、jH:因子[-]、Pr:プラントル数[-]
μ:流体粘度[cp]、μw:壁面での流体粘度[cp]
"熱交換器設計ハンドブック, 尾花英明 ,(2000)"を参照
jH因子は下の計算図表から読み取った値を使用します。

この式の適用範囲はかなり広く、レイノルズ数に関しては図表の範囲であれば適用できます。
層流にも乱流にも適用できる数少ない式だと思います。
Hausenの式
$$Nu=\frac{h_{i}D}{λ}=0.116[Re^{\frac{2}{3}}-125]Pr^{\frac{1}{3}}[1+(\frac{D}{L})^{\frac{2}{3}}](\frac{μ}{μ_{w}})^{0.14}$$
適用範囲
$$2,320≦Re≦100,000$$
$$0.6≦Pr≦500$$
$$\frac{L}{D}≧1$$
Nu:ヌセルト数[-]、hi:管内側境膜伝熱係数[W/(m2K)]、D:管内径[m]、
λ:流体の熱伝導度[W/mK]、Re:レイノルズ数[-]、Pr:プラントル数[-]
L:配管長[m]、μ:流体粘度[cp]、μw:壁面での流体粘度[cp]
"熱交換器設計ハンドブック, 尾花英明 ,(2000)"を参照
遷移域から乱流までのそこそこ広い範囲に適用できる式です。
各式の計算比較
上で紹介した3種類の式とaspentech社がリリースしている熱交換器設計ソフト"Aspen Exchanger Design and Rating"(以下EDR)で試しに計算して境膜伝熱係数を比較してみました。
伝熱管径20A、伝熱管長さ5m、流体は水で、配管内の平均流速を変化させて計算しました。
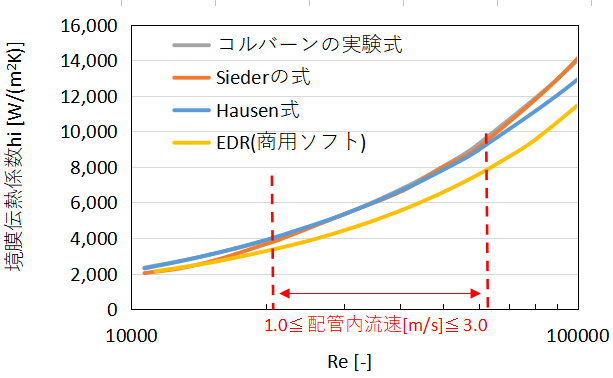
上のグラフに結果を示します。
どの計算手法でも似たような境膜伝熱係数の推移になっています。
コルバーンの実験式とSiederの式はほぼ同じ値を示しています。
Siederの式は対数グラフからjHを読み取るのが地味に難しかったです。
EDRはチューブ長5mを細かく分割して各区間で厳密に計算している点、ソフトの仕様上単管ではなく二重管のような形状で計算したため、他の式とは前提条件が少し違う点はご容赦ください。
EDRの境膜伝熱係数は全体的に少し小さめとなっています。
設計者としては伝熱係数を過剰に見積もるよりは少なめに見積もる方が後々のトラブルは少ないかなと思います。
また、上のグラフに示していますが冷却水等の液体の配管内流速はだいたい1.0~3.0m/sの間で設計することが多いです。レイノルズ数でいうと赤点線の間です。
流速が遅いと伝熱性能が悪化しますし、かつ配管内に汚れが付着しやすくなります。
逆に流速が速いと圧力損失が無駄にかかり過ぎるので良くありません。
