概要
化学反応速度を求めるためには、その反応の次数を知ることが必要です。
有名な反応ですでに反応次数が知られていればよいですが、そうでない場合は実験データから反応次数を決定する必要があります。
この記事では反応次数の決定手法について解説しています。
反応次数の算出方法
ここでは主要な算出方法である微分法と積分法について解説します。
微分法
微分法は実験データを図微分、もしくは数値微分することで反応次数を決定する手法です。
例えば、
$$-\frac{d[A]}{dt}=k[A]^{m}[B]^{n}・・・(1)$$
(1)式のような反応の次数mを算出することを考えます。
(1)式の両辺対数を取ると、
$${\rm{ln}}(-\frac{d[A]}{dt})={\rm{ln}}k+m{\rm{ln}}[A]+n{\rm{ln}}[B]・・・(2)$$
(2)式となります。
(2)式について縦軸ln(-d[A]/dt)、横軸ln[A]でプロットすれば直線が得られ、この傾きが反応次数mとなります。
同様に反応次数nについて求める場合は、
$${\rm{ln}}(-\frac{d[B]}{dt})={\rm{ln}}k+m{\rm{ln}}[A]+n{\rm{ln}}[B]・・・(3)$$
(3)式について縦軸ln(-d[B]/dt)、横軸ln[B]でプロットすればよいですね。
したがって、あとは左辺の反応速度であるd[A]/dtやd[B]/dtをどう算出するか、という話になります。
実験データとして普通得られるのは濃度[A]、[B]とデータを取得した時間のみなので、これらの値から反応速度を算出する必要があります。
手法は様々ありますが、ここでは3つ挙げます。
接線の作図による算出
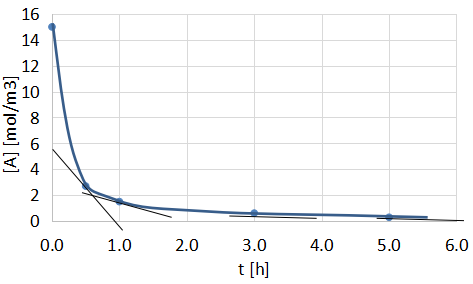
縦軸に注目成分の濃度、横軸に反応時間をプロットし、各点を通るように曲線を引きます。
その後各点で接線を引き、傾きを求めます。この接線の傾きがその時間における反応速度となります。
あとは(2)式にしたがって縦軸ln(-d[A]/dt)、横軸ln[A]でプロットし、直線の傾きを求めれば反応次数が得られます。
メリット
- 作図で求められるため簡便でわかりやすい
デメリット
- 作図の精度で誤差がかなり出やすい
- 傾きが極端に大きい(もしくは小さい)点は、誤差が出やすいため使用しづらい(上図でいうとt=0.0, 3.0, 5.0の点)
今回はt=0.5, 1.0の2点が頼りになりそうです。
ただし、本来はプロットの数が少ないのは好ましくありません。実験データを取り直せる場合は、作図しやすい時間のデータを追加で取得すべきでしょう。
曲線の微分による算出
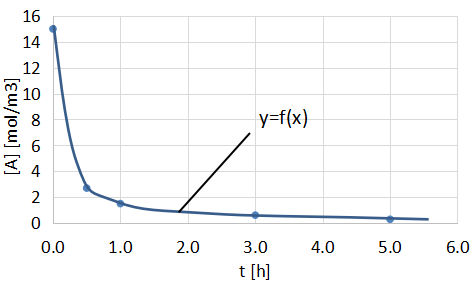
各点を通るような曲線を引き、その曲線を多項式等で近似します。
その多項式を微分することで任意の時間の反応速度を得ることができます。
後は同様に(2)式について直線プロットすることで反応次数が得られます。
メリット
- データをうまく表現できる近似曲線の式が得られれば、任意の時間における反応速度が得られるため算出精度が高くなる。
デメリット
- 近似曲線を得ることが難しい。フィッティングには数学的な知識が必要な場合もある。
中点による算出
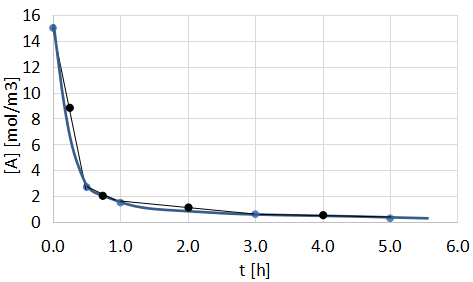
各実験データの中点の反応速度を算出して反応次数を求める手法です。
メリット
- 表計算ソフト等で簡単に中点の反応速度を計算できる。
- 作図がいらない。
デメリット
- 2点のデータを取得した時間が離れている場合、誤差が大きくなる。
- n個のプロットに対してn-1個の反応速度しか得られないため、取得データ数が少ない場合は誤差が大きくなる。
積分法
実測データと積分形速度式を比較して、相関が一致する次数を見極める手法です。
各反応次数で濃度と時間がどのような関係式になるか知っておく必要があります。
0次反応
0次反応の場合、
$$-\frac{d[A]}{dt}=k[A]^{0}=k・・・(4)$$
(4)式となります。
(4)式をt=0~t,[A]=[A]0~[A]まで積分すると、
$$[A]=[A]_{0}-kt・・・(5)$$
(5)式となります。
したがって、縦軸に[A]、横軸に時間tをプロットして直線が得られれば0次反応であることがわかります。
1次反応
1次反応の場合、
$$-\frac{d[A]}{dt}=k[A]^{1}・・・(6)$$
(6)式となります。
(6)式をt=0~t,[A]=[A]0~[A]まで積分すると、
$${\rm{ln}}(\frac{[A]}{A_{0}})=-kt・・・(7)$$
(7)式となります。
したがって、縦軸にln[A]、横軸に時間tをプロットして直線が得られれば1次反応であることがわかります。
2次反応
2次反応の場合、
$$-\frac{d[A]}{dt}=k[A]^{2}・・・(8)$$
(8)式となります。
(8)式をt=0~t,[A]=[A]0~[A]まで積分すると、
$$\frac{1}{[A]}=\frac{1}{[A]_{0}}+2kt・・・(9)$$
(9)式となります。
したがって、縦軸に1/[A]、横軸に時間tをプロットして直線が得られれば2次反応であることがわかります。
おわりに
反応次数の決定手法について解説しました。どの手法も一長一短で、使い分けが必要です。
ただ、実務では反応次数が整数ではないこともあるため、微分法を使用することが多いでしょうか。
