概要
化学プラントの装置設計をするうえで、正しい物性を使用して計算することは非常に重要です。
プラントの主要な装置である蒸留塔や熱交換器の設計には、特に気液平衡データの精度が重要になってきます。
気液平衡データの取得は、
- 実験してデータを取得する
- 文献データを参照する
主に上の方法が挙げられますが、どちらもデータの精度が気になるところです。
本記事では気液平衡データの熱力学的健全性を確認するテストについて紹介します。
このテストに合格すれば、そのデータは熱力学的な整合性の必要条件を満たしていると判断でき、精度が高いと予想されます。
基礎理論
熱力学的健全性評価の基礎となるのはギブス・デュエムの式です。
まず過剰ギブス自由エネルギーを温度T、圧力P、組成nの関数として全微分します。
$$\begin{align}\frac{dG^E}{RT}&=\Bigl(\frac{∂G^E/(RT)}{∂T}\Bigr)_{P,n_{i}}dT+\Bigl(\frac{∂G^E/(RT)}{∂P}\Bigr)_{T,n_{i}}dP\\&+\sum \Bigl(\frac{∂G^E/(RT)}{∂n_{i}}\Bigr)_{T,P,n_{j}}dn_{i}・・・(1)\end{align}$$
(1)式をギブス・デュエムの式といい、詳細は以下の記事で解説しています。
-

【ギブス・デュエムの式】を解説:熱力学的健全性評価の基礎式
任意の状態量mについて成り立つ(1)式のような熱力学的な関係をギブス・デュエム(Gibbs–Duhem)の式といいます。応用的には熱力学的測定データの健全性の確認に使用されています。
続きを見る
次に、ギブス自由エネルギーの関係式を過剰ギブス自由エネルギーに適用すると、
$$dG^{E}=-S^{E}dT+V^{E}dP・・・(2)$$
(2)式が成り立ちます。
温度、組成一定条件下では、
$$\Bigl(\frac{∂G^E}{∂P}\Bigr)_{T,n_{i}}=V^{E}・・・(3)$$
(3)式となります。
次に、ギブス-ヘルムホルツの式を過剰ギブス自由エネルギーに適用すると、
$$\Bigl(\frac{∂G^E/T}{∂T}\Bigr)_{T,n_{i}}=-\frac{H^{E}}{T^2}・・・(4)$$
(4)式となります。
次に、活量係数の定義から、
$$\Bigl(\frac{∂G^E/(RT)}{∂n_{i}}\Bigr)_{T,P,n_{j}}={\rm{ln}}γ・・・(5)$$
(5)式となります。
ここで2成分系を前提とし、(3)、(4)、(5)式を(1)式に代入すると、
$$\frac{dG^E}{RT}=-\frac{H^{E}}{RT^2}dT+\frac{V^{E}}{RT}dP+({\rm{ln}}γ_{1})dn_{1}+({\rm{ln}}γ_{2})dn_{2}・・・(6)$$
(6)式となります。両辺をモル数nで割り、dx2=-dx1の関係を使用し整理すると、
$$\frac{dg^E}{RT}=-\frac{h^{E}}{RT^2}dT+\frac{v^{E}}{RT}dP+{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}・・・(7)$$
(7)式となります。
(7)式をx1=0~1まで積分すると、熱力学的健全性評価に使用できる基礎式(8)が得られます。
$$\int_{x_{1}=0}^{x_{1}=1}\frac{dg^E}{RT}=\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}-\int_{x_{1}=0}^{x_{1}=1}\frac{h^{E}}{RT^2}dT+\int_{x_{1}=0}^{x_{1}=1}\frac{v^{E}}{RT}dP=0・・・(8)$$
熱力学的健全性テスト
まず、熱力学的健全性テストに合格したからといって、必ずしも健全で精度が良いデータであるとは言い切れないことを知っておくべきです。
熱力学的健全性テストでは、主に2成分の過剰ギブス自由エネルギーgEあるいは活量係数γの実測値を使用して評価します。
このとき、うまい具合に成分1と成分2の測定値の誤差が打ち消し合うことで、本来全く健全ではないデータが合格と判断されることがあります。
したがって、テストに合格したデータは熱力学的健全性の必要条件を満たしていますが、十分条件を満たしていないことに留意すべきです。
Redlich-Kister test
数ある熱力学的健全性テストの中でも、比較的簡単なものがRedlich-Kister testです。
定温・定圧
(8)式から、
$$\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}=\int_{T(x_{1}=0)}^{T(x_{1}=1)}\frac{h^{E}}{RT^2}dT-\int_{P(x_{1}=0)}^{P(x_{1}=1)}\frac{v^{E}}{RT}dP・・・(9)$$
(9)式となります。
定温・定圧条件下では、右辺の項が全てゼロになるため、
$$\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}=0・・・(10)$$
(10)式が成立すれば熱力学的健全性を満たすことになります。
(10)式が具体的に意味するところは、グラフを書いてみればわかります。
縦軸lnγ1/γ2、横軸x1としてグラフを書くと、
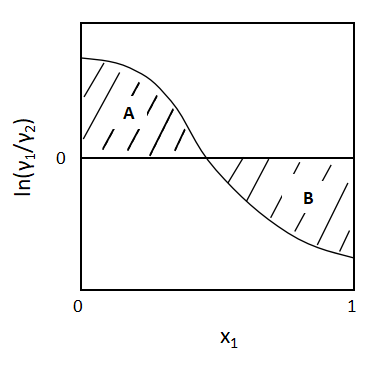
上図のようなグラフになります。
このグラフのx1軸の上下に面積A、Bができ、これらの面積が等しくなる、つまりA=Bとなると(10)式が成立します。
ただし、実際のデータではぴったりとA=Bとなることはなく、ある程度の偏差を生じるはずです。
この偏差の許容基準として、
$$D=100\frac{\left|A-B\right|}{A+B}<10・・・(11)$$
(11)式のようにD<10、つまり偏差が10%以下であればテストに合格したとみなします。
一方で、定温・定圧データを気液平衡で扱うことはほとんどないため、定温・定圧の仮定はあまり意味がありません。
定温
定温では(9)式において右辺の第一項がゼロとみなせるため、
$$\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}=-\int_{P(x_{1}=0)}^{P(x_{1}=1)}\frac{v^{E}}{RT}dP・・・(12)$$
(12)式が成り立ちます。
そのため、厳密には混合による体積変化を考慮する必要があります。
しかし、一般に右辺の体積変化の項は左辺に比べて微小で、無視してもそれほど差し支えありません。
したがって、定温データでは簡易的に、
$$\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}=0・・・(10)$$
(10)式で計算してよいでしょう。
ここでは例として、エタノール-水の2成分系における定温データで計算してみましょう。
| 温度[K] | 圧力[Pa] | エタノール 液相組成x1[-] | エタノール 気相組成y1[-] |
| 423.7 | 532,800 | 0.0137 | 0.1100 |
| 423.7 | 582,500 | 0.0256 | 0.2017 |
| 423.7 | 622,900 | 0.0415 | 0.2390 |
| 423.7 | 629,700 | 0.0427 | 0.2587 |
| 423.7 | 760,800 | 0.1204 | 0.4009 |
| 423.7 | 845,900 | 0.2507 | 0.4881 |
| 423.7 | 855,000 | 0.2825 | 0.4975 |
| 423.7 | 898,700 | 0.3926 | 0.5603 |
| 423.7 | 948,800 | 0.5669 | 0.6430 |
| 423.7 | 964,600 | 0.6417 | 0.6960 |
| 423.7 | 972,100 | 0.7094 | 0.7390 |
| 423.7 | 987,900 | 0.7947 | 0.8071 |
| 423.7 | 986,300 | 0.9980 | 0.9981 |
"Cristino, A. F.; Rosa, S.; Morgado, P.; Galindo, A.; Filipe, E. J. M.; Palavra, A. M. F.; Nieto de Castro, C. A. Fluid Phase Equilib., 2013, 341, 48-53"
まず実測データから活量係数γを求めます。
$$Py_{1}=P_{1}^{0}x_{1}γ_{1}・・・(13)$$
$$Py_{2}=P_{2}^{0}x_{2}γ_{2}・・・(14)$$
P:全圧[Pa]、P10、P20:成分1,2の純物質蒸気圧[Pa]
y1、y2:成分1,2の気相のモル分率[-]、x1、x2:成分1,2の液相のモル分率[-]
(13)、(14)式を使用すれば活量係数γを求めることができます。
求めたγ1、γ2を使用して、縦軸ln(γ1/γ2)、横軸x1のグラフを作成すると以下のようになります。
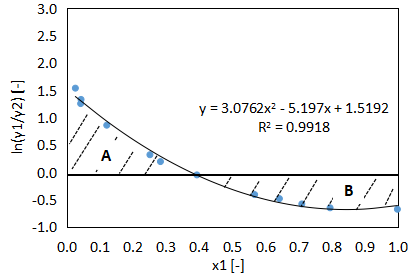
次にこのグラフのA、Bの面積を算出します。
面積を求められれば手法は何でもよいですが、
- 近似曲線を作成し積分する。
- 区間分割し、台形近似等を利用する。
以上のような方法が比較的簡便でしょう。
本記事では、近似曲線を作成し積分する手法でやってみます。
エクセルの近似曲線作成機能を使用し、なるべく積分しやすい関数を作ります。
簡易的にグラフの縦軸をy、横軸をxと表現すると、
$$y=3.0762x^{2}-5.197x+1.5192・・・(15)$$
今回は二次関数でそれなりに良いR2乗値が得られました。
次に、積分するには関数とx軸との交点の情報が必要です。
(15)式でy=0として解きますが、解が2つあるため0<x<1の間にある方を選びましょう。
$$x=0.376・・・(16)$$
(16)式から積分区間がわかりますので積分できるようになります。
まず、Aの面積は、
$$\begin{align}A&=\int_{0}^{0.376}(3.0762x^{2}-5.197x+1.5192)dx\\&≒0.258・・・(17)\end{align}$$
となります。
続いて、Bの面積は、
$$\begin{align}B&=-\int_{0.376}^{1}(3.0762x^{2}-5.197x+1.5192)dx\\&≒0.312・・・(18)\end{align}$$
となります。
A、Bの面積の値がわかれば、あとは(11)式を使用して健全性を確認できます。
$$D=100\frac{\left|0.258-0.312\right|}{0.258+0.312}≒9.45<10・・・(11)$$
Dの計算値が10未満となりましたので、今回使用したデータはRedlich-Kisterのテストに合格しました。
定圧
定圧データの場合、混合による体積変化がゼロになるため、(9)式の第二項がゼロとなります。
よって定圧では
$$\int_{x_{1}=0}^{x_{1}=1}{\rm{ln}}\frac{γ_{1}}{γ_{2}}dx_{1}=\int_{T(x_{1}=0)}^{T(x_{1}=1)}\frac{h^{E}}{RT^2}dT・・・(19)$$
(19)式が成立します。
したがって、定圧データでは混合熱の影響も考慮する必要があります。
混合熱がほとんど発生しない系であれば、右辺をゼロと近似することも可能ですが、非理想性がそれなりに確認される系では混合熱が少なからず発生し、無視できない影響を与えます。
そのため(19)式で評価するためには使用するデータの各気液平衡状態における混合熱データが必要となりますが、そのようなデータが文献にあることはほとんどなく、実測するのも難しい作業となります。
このような背景から、定圧データを(19)式でテストすることは実質的に困難で、定圧データの評価には別のテスト手法を使用した方がよいでしょう。
Herington test
定圧データを評価するための手法の1つとして、Herington testが挙げられます。
まずRedlich-Kister testと同様に縦軸ln(γ1/γ2)、横軸x1のグラフを作成し、面積A、Bを求めます。
次にA、Bの値及び系の最高温度Tmax[K]、最低温度Tmin[K]を使用して、
$$D=100\left|\frac{A-B}{A+B}\right|・・・(20)$$
$$J=150\left|\frac{θ}{T_{min}}\right|・・・(21)$$
$$θ=T_{max}-T_{min}・・・(22)$$
D、Jの値を求めます。
ちなみに、非共沸系であれば最高温度Tmax、最低温度Tminはそれぞれ純物質の沸点となります。
最終的に、(23)式が成立すればHerington testに合格したとみなします。
$$\left|D-J\right|<10・・・(23)$$
ここでは、エタノール-水の2成分系における定圧データで計算してみましょう。
| 温度[K] | 圧力[Pa] | エタノール 液相組成x1[-] | エタノール 気相組成y1[-] |
| 373.15 | 101320 | 0.000 | 0.000 |
| 368.38 | 101320 | 0.018 | 0.165 |
| 367.05 | 101320 | 0.028 | 0.221 |
| 363.90 | 101320 | 0.051 | 0.321 |
| 360.69 | 101320 | 0.081 | 0.403 |
| 358.51 | 101320 | 0.125 | 0.474 |
| 357.03 | 101320 | 0.169 | 0.513 |
| 355.92 | 101320 | 0.228 | 0.551 |
| 354.25 | 101320 | 0.335 | 0.609 |
| 353.07 | 101320 | 0.474 | 0.646 |
| 352.51 | 101320 | 0.556 | 0.683 |
| 351.87 | 101320 | 0.664 | 0.732 |
| 351.48 | 101320 | 0.756 | 0.792 |
| 351.31 | 101320 | 0.893 | 0.892 |
| 351.40 | 101320 | 0.922 | 0.911 |
| 351.41 | 101320 | 0.961 | 0.954 |
| 351.45 | 101320 | 1.000 | 1.000 |
"Peng, Yong; Lu, Xiuyang; Liu, Baojian; Zhu, Ju Fluid Phase Equilib., 2017, 448, 128-134 Separation of azeotropic mixtures (ethanol and water) enhanced by deep eutectic solvents"
Redlich-Kister testと同様に活量係数を算出し、縦軸ln(γ1/γ2)、横軸x1のグラフを作成し、A、Bの面積を求めます。
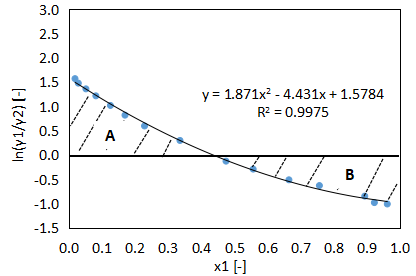
面積計算の詳細は割愛しますが、
- A=0.319
- B=0.332
となりました。
(20)、(21)、(23)式から、
$$D=100\left|\frac{0.319-0.332}{0.319+0.3332}\right|≒2.064・・・(20)$$
$$J=150\left|\frac{373.15-351.45}{351.45}\right|≒9.262・・・(21)$$
$$\left|2.064-9.262\right|=7.198<10・・・(23)$$
となり、今回使用したデータはHerington testに合格しました。
Van Ness test
Redlich-Kister testとHerington testは面積テストをベースとした手法ですが、それ以外のテスト手法もあります。
Van Ness testは実測値と推算値の誤差を比較する手法で、Area test(面積テスト)に対してpoint-to-point testと呼ばれています。
まず、(13)、(14)式から実測値の活量係数γ*を算出します。
$$Py_{1}=P_{1}^{0}x_{1}γ_{1}^{*}・・・(13)$$
$$Py_{2}=P_{2}^{0}x_{2}γ_{2}^{*}・・・(14)$$
次に推算値の活量係数γを求めます。
推算では活量係数モデルを使用するのが一般的です。
ここでは、NRTLを例に挙げます。
$${\rm{ln}}γ_{1}=x_{2}^{2}\biggl(τ_{21}\biggl(\frac{G_{21}}{x_{1}+x_{2}G_{21}}\biggr)^{2}+\frac{τ_{12}G_{12}}{(x_{2}+x_{1}G_{12})^{2}}\biggr)・・・(24)$$
$${\rm{ln}}γ_{2}=x_{1}^{2}\biggl(τ_{12}\biggl(\frac{G_{12}}{x_{2}+x_{1}G_{12}}\biggr)^{2}+\frac{τ_{21}G_{21}}{(x_{1}+x_{2}G_{21})^{2}}\biggr)・・・(25)$$
(25)式がNRTLを使用した場合の活量係数γの推算式です。
(24)、(25)式においてτ12、τ21、G12、G21は実測値からフィッティングして決定します。
このフィッティングは最小二乗法等を使用しますが、本記事の主題ではないので過程は省略します。
次に求めた実測値γ*と推算値γを使用し、
$$δ{\rm{ln}}\frac{γ_{1}}{γ_{2}}={\rm{ln}}\frac{γ_{1}^{*}}{γ_{2}^{*}}-{\rm{ln}}\frac{γ_{1}}{γ_{2}}・・・(25)$$
各データの差分を求めます。
最後にδln(γ1/γ2)の二乗平均平方根(RMS)を求めます。
このRMSの値により健全性の程度を評価します。
Van Nessは熱力学的健全性を10段階に分けており、以下の表に示します。
| 指標 | RMS |
| 1 | >0 |
| 2 | >0.025 |
| 3 | >0.050 |
| 4 | >0.075 |
| 5 | >0.100 |
| 6 | >0.125 |
| 7 | >0.150 |
| 8 | >0.175 |
| 9 | >0.200 |
| 10 | >0.225 |
指標1が最も健全性が良く、指標10が最も悪いデータとなります。
少なくともRMSが指標10より大きくなる場合は、健全性がかなり悪いと判断できます。
またモデルの特徴として、Van Ness testは熱力学的健全性を評価する指標というよりは、データが使用した活量係数モデルに適合しているかを判断していると言えます。
したがって、あるモデルで健全性が悪くても、別のモデルで健全性が良くなる可能性もあります。
健全性テストの扱いについて
熱力学的健全性テストを実施し、合格したデータのみを使用して装置設計するのが最も合理的です。
しかし、世の中には健全性の悪い文献データが数多く存在するため、理想通りにはいきません。
個人的に、熱力学的健全性テストが意味を持つのは、何回もデータ取得をやり直せる環境がある場合のみだと考えています。
自分でデータを取るにしろ、誰かにデータを取ってもらうにしろ、時間とコストがかかるものです。
特に時間的制約があるなかでデータの再取得にスケジュールを割くのはかなり困難です。
また、実際には実験してデータを取ることすらできないことも多々あります。その場合には、手持ちにあるデータでなんとか気液平衡を計算するしかありません。
手持ちのデータが健全性テストで不合格であった場合の対応としては、
大きく3つに分けられます。
個人的な経験として、3つ目の不合格なデータを使用する場合が実際の気液平衡に最も近いことが多いです。
ということで、データを再取得できない環境の場合は、健全性テストの合否に関わらず手持ちのデータを使用するのがベターであるため、健全性テストを実施する意味が薄いのでは、と考えています。
おわりに
熱力学的健全性テストについて解説しました。
使用するデータの精度が疑われる場合にはぜひ試してみましょう。
