概要
Runge-Kutta法(ルンゲクッタ法)は常微分方程式を解く手法の1つです。
同じく常微分方程式を解く手法としてEuler法がありますが、その手法よりも計算精度が優れていることから数値計算ソフトのデフォルトの解法として採用されていることもあります。
Euler法では曲線の傾きの変化が大きい場合には予測精度が落ちる、あるいは刻み幅を相当細かくしないと精度を維持できない等の問題があります。
しかしRunge-Kutta法ではそのような曲線の計算にも強く、そこまで刻み幅を細かくしなくとも良い精度が出ます。
本記事ではRunge-Kutta法の計算手法について解説します。加えて、回分式反応器の一次反応に関する例題を解いてみて、Euler法とRunge-Kutta法の計算精度を比較してみました。
Runge-Kutta法の計算手法
原理と計算式
$$\frac{dy}{dx}=f(x,y)・・・(1)$$
Euler法を(1)式に適用すると、
$$y(x_{n+1})=y(x_{n})+hf(x_{n},y(x_{n}))・・・(2)$$
(2)式のような形で逐次計算することができます。
Runge-Kutta法はEuler法をさらに発展させた計算手法となっています。
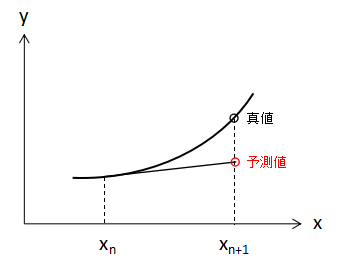
Euler法では上図のように初期値xnの値のみを使用して次のxn+1の値を予測しています。
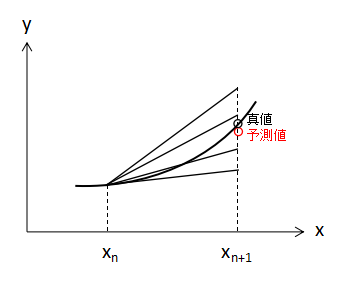
これに対してRunge-Kutta法ではEuler法で算出した傾きを含めて合計4つの手法で傾きを算出し、重みづけして平均を取ることで最終的な予測値としています。
1つ目の傾き
まず1つ目の傾きはEuler法と全く同様の手法で計算します。
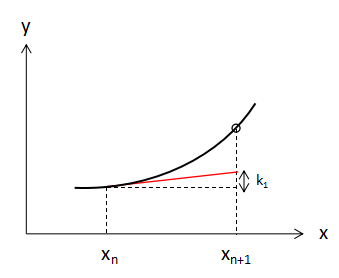
上図のようにxnからxn+1へ変化したときのf(x,y)の増加量をk1とすると、
$$k_{1}=hf(x_{n},y_{n}) ・・・(3) $$
(3)式となります。
2つ目の傾き
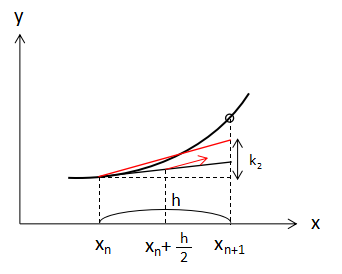
次にk1の値を利用して、x=xn+h/2、y=yn+k1/2の点から傾きを求めると、
$$f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{1}}{2})$$
となります。
この傾きで、初期値である点(xn,yn)から線を引いたときの f(x,y) の増加量をk2とすると、
$$k_{2}=h×f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{1}}{2})・・・(4) $$
(4)式となります。
3つ目の傾き

次も同じ要領でk2の値を利用して、 x=xn+h/2、y=yn+k2/2の点から傾きを求めると、
$$f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{2}}{2})$$
となります。
この傾きで、初期値である点(xn,yn)から線を引いたときの f(x,y) の増加量をk3とすると、
$$k_{3}=h×f(x_{n}+\frac{h}{2},y_{n}+\frac{k_{2}}{2})・・・(5) $$
(5)式となります。
4つ目の傾き
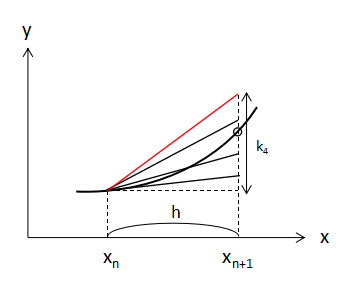
最後はk3の値を利用して、初期値である点(xn,yn)から線を引いたときの f(x,y) の増加量をk4とすると、
$$k_{4}=h×f(x_{n}+h,y_{n}+k_{3})・・・(6) $$
(6)式となります。
4つの傾きの重みづけ平均
これまで求めてきた増加量k1~k4の重みづけ平均を取ることで、最終的な増加量kを決定します。
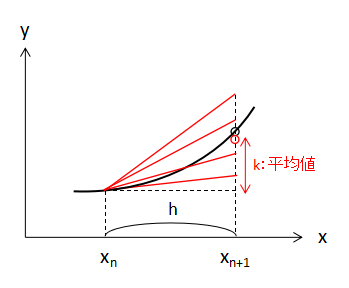
計算式は、
$$ k=\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}・・・(7) $$
(7)式となります。
k2とk3が2倍の重みづけとなっているのは、一般的にk2とk3の値が真の値に近いと考えられるためです。
したがって、Runge-Kutta法における逐次計算式は、
$$ y_{n+1}=y_{n}+\frac{k_{1}+2k_{2}+2k_{3}+k_{4}}{6}・・・(8) $$
(8)式となります。
例題:回分式反応器の一次反応
計算条件
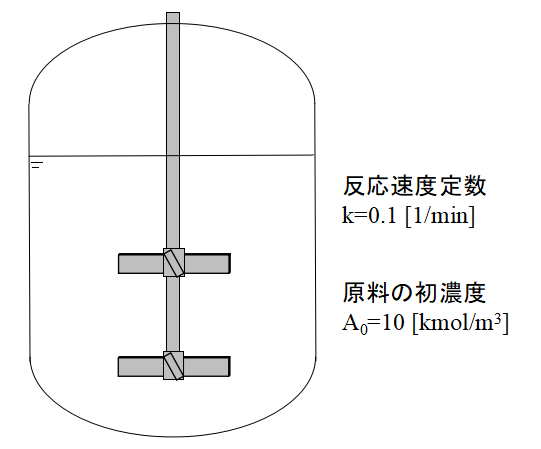
例題では上図に示すような回分式反応器内の反応による原料濃度Aの変化を計算してみます。
バッチ反応器であるため流体の流入流出はないものとします。
反応は一次反応とします。
なお、その他の条件として、
- 反応速度定数k:0.1 1/min
- 原料の初濃度:10mol/L
以上の条件がわかっているものとします。
基礎式の導出
タンク内の原料濃度Aについて物質収支を取ると、
$$\frac{dA}{dt}=-kA・・・(9)$$
(9)式となります。
簡単ですが、これで基礎式の導出は終了です。
(9)式は手計算で積分することができるので、今回の例題を解くだけならRunge-Kutta法は必要ありません。
しかし実務では単なる一次反応を扱うことはあまりなく、複雑な反応を複数扱うことが多いためRunge-Kutta法等による数値解法はほぼ必須です。
Runge-Kutta法の適用
今回もExcelで計算してみます。
まず時間刻みhを決定します。とりあえずh=1minと設定します。
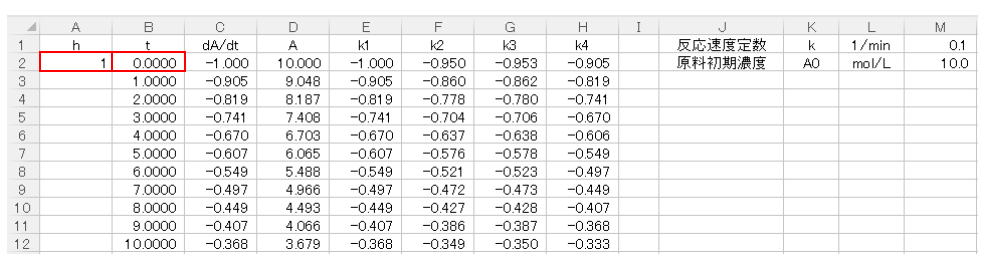
B2セルには時間の初期値としてt=0を入力し、B3セルはB2セル+$A$2セルと入力して時間変化を表わします。
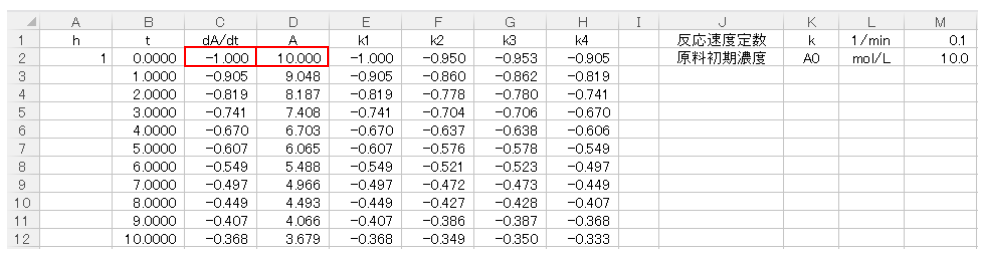
続いてC2セルに(9)式の右辺を入力します。原料濃度AはDの列に入力していき、D2セルにはAの初濃度10mol/Lを入力します。
次に原料濃度AをRunge-Kutta法で表すために、k1,k2,k3,k4を算出します。
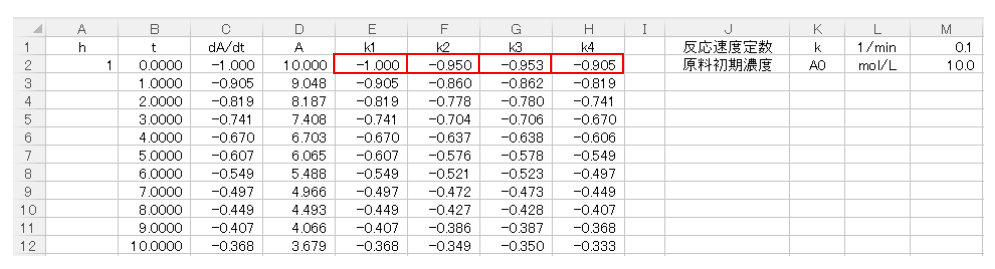
k1は(3)式から求まりますのでE2セルに
$$E2セル=A2セル×C2セル$$
と入力します。
続いてk2も(4)式から算出できますので、F2セルに
$$F2セル=A2セル×(-M1セル×(D2セル+E2セル/2))$$
と入力します。
後は同様にk3,k4も(5),(6)式に従って、
$$G2セル=A2セル×(-M1セル×(D2セル+F2セル/2))$$
$$H2セル=A2セル×(-M1セル×(D2セル+G2セル))$$
と入力します。
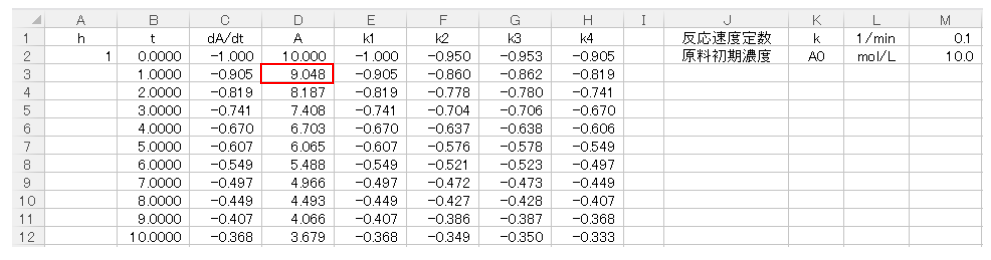
次にD3セルに(8)式を入力して1ステップ目の計算が終わります。D3セルには、
$$D3セル=D2セル+(E2セル+2×F2セル+2×G2セル+H2セル)/6$$
と入力します。
後は同じ計算をコピーして下の行に張り付ければ繰り返し計算が可能です。
今回はとりあえずt=10minまでで計算しました。
結果の比較
今回のRunge-Kutta法による計算結果を、Euler法による計算結果、解析解と比較してみました。
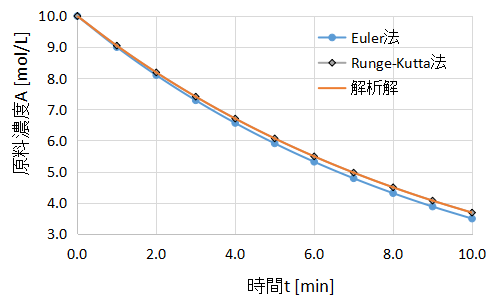
上図に比較結果を示します。
Euler法と解析解には少しずれがある一方で、Runge-Kutta法と解析解はぴったり一致していますね。
Runge-Kutta法の計算精度の高さがよく表れています。
まとめ
常微分方程式の解法の1つであるRunge-Kutta法について解説しました。
Euler法と比較して計算手法は少し複雑になりますが、一度理解してしまえば2回目からはほぼコピペで使えるようになると思います。
化学工学はそれほどシビアに精度を要求されない分野ではあるものの、可能な限り計算精度は上げたいですね。
