概要
多変数Newton-Raphson法の原理は1変数の場合と同じで、以下の記事で1変数の場合の解説や計算例を出しています。
とは言っても、実際に計算するとなると1変数と多変数では勝手が違います。
本記事では気液フラッシュ計算を例としてPythonで多変数のNewton-Raphson法を解いてみました。
多変数のNewton-Raphon法
計算式
わかりやすさ重視で2変数の場合の計算式を紹介します。
$$f(x,y)=0・・・(1)$$
$$g(x,y)=0・・・(2)$$
(1),(2)式を連立させて変数x,yを求めます。
この連立方程式を初期値x0、y0として繰り返し計算を行なったとき、i回目の近似解をxi、yiとします。
このとき、(1)式をxi、yiの周りでTaylor展開すると、
$$f(x_{i}+Δx,y_{i}+Δy)=f(x_{i},y_{i})+\frac{Δx}{1!}\frac{∂f}{∂x}+ \frac{Δy}{1!}\frac{∂f}{∂y}+・・・ =0・・・(3)$$
(3)式のようになります。
(3)式の・・・以降の微小量Δx,Δyの2乗の項は切り捨てて1乗までの項のみで整理します。
$$Δx\frac{∂f}{∂x}+ Δy\frac{∂f}{∂y}=-f(x_{i},y_{i})・・・(4)$$
(2)式も同じ操作を行なうと、
$$Δx\frac{∂g}{∂x}+ Δy\frac{∂g}{∂y}=-g(x_{i},y_{i})・・・(5)$$
それぞれ(4),(5)式となります。(4),(5)式をΔx、Δyを解とするように行列式へと変形すると、
\(\begin{pmatrix}\frac{∂f}{∂x}& \frac{∂f}{∂y}\\\frac{∂g}{∂x}& \frac{∂g}{∂y}\end{pmatrix}
\begin{pmatrix}Δx\\Δy\end{pmatrix}
=\begin{pmatrix}-f(x_{i},y_{i})\\-g(x_{i},y_{i})\end{pmatrix}\) ・・・(6)
(6)式となります。ちなみに(6)式の偏微分で表される行列をヤコビ行列といいます。
あとはこの(6)式を解いてΔx,Δyを算出し、
$$x_{i+1}=x_{i}+Δx・・・(7)$$
$$y_{i+1}=y_{i}+Δy・・・(8)$$
(7),(8)式に代入することでxとyの繰り返し計算をすることができ、Newton-Raphson法を行なえます。
行列式の計算法
多変数Newton-Raphson法は(6)式をどうやって解くかが重要です。
上の例のように2変数であれば2×2のヤコビ行列で済むので手計算でもやれる範囲ですが、3変数なら3×3行列、4変数なら4×4行列と計算量が増大します。
今回Pythonで計算するにあたって多変数Newton-Raphson法について他の記事を調査しましたが、ヤコビ行列を自分の頭で計算して微分結果をPythonに入力しているような記事が多かったです。
せっかくパソコンに計算させるならヤコビ行列含めて自動で計算できるようにしないと意味がないでしょう。
本記事ではヤコビ行列を自動で計算できるようなコードを書いています。
また、(6)式の解法は逆行列を算出して解いています。変数の数が多くなると逆行列の計算負荷が高くなりますが、今回の例で挙げるフラッシュ計算程度なら問題ありませんでした。
Pythonでの計算法
計算条件
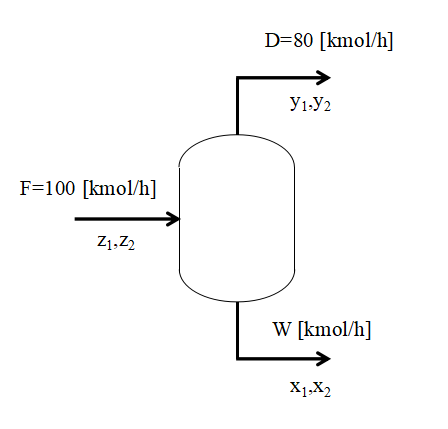
上図に示すようなフラッシュドラムに原料をフィードしてフラッシュさせる系を考えます。
前提条件を以下に示します。
- フィード流量F:100[kmol/h]
- 出口ガス流量D:80[kmol/h]
- フィード中の成分1組成z1:0.2[-]
- ドラム内圧力P:101.3[kPaA]
成分1,2のAntoine式は、
$${\rm{ln}}P_{10}=A_{1}-\frac{B_{1}}{C_{1}+T}・・・(9)$$
A1=20.7936、B1=2788.51、C1=-52.36
$${\rm{ln}}P_{20}=A_{2}-\frac{B_{2}}{C_{2}+T}・・・(10)$$
A2=20.9065、B2=3096.52、C2=-53.67
(9)、(10)式を使用します。温度Tはケルビンです。
計算式
まず成分1,2について物質収支を取ります。
$$Fz_{1}=Dy_{1}+Wx_{1}・・・(11)$$
$$Fz_{2}=Dy_{2}+Wx_{2}・・・(12)$$
次に各ストリームでの組成について式を立てます。
$$x_{1}+x_{2}=1・・・(13)$$
$$y_{1}+y_{2}=1・・・(14)$$
$$z_{1}+z_{2}=1・・・(15)$$
次に気液平衡の計算式を立てます。Raoultの法則が成り立つとして、
$$Py_{1}=P_{10}x_{1}・・・(16)$$
$$Py_{2}=P_{20}x_{2}・・・(17)$$
後は計算条件で与えられた条件を加えます。
Antoine式から、
$${\rm{ln}}P_{10}=A_{1}-\frac{B_{1}}{C_{1}+T}・・・(9)$$
$${\rm{ln}}P_{20}=A_{2}-\frac{B_{2}}{C_{2}+T}・・・(10)$$
計算条件から、
$$F=100・・・(18)$$
$$D=80・・・(19)$$
$$z_{1}=0.2・・・(20)$$
$$P=101300・・・(21)$$
となり、全部で13式となりました。
変数は、x1、x2、y1、y2、z1、z2、F、D、W、P10、P20、P、Tで式の数と同じ13変数ですね。これで理論上は解くことが可能です。
ただし、実際に手計算でやってみると大変だと思います。Antoine式は温度が与えられていると簡単に各成分の蒸気圧P10、P20が求まるのですが、今回は与えられていませんので収束計算で解く必要があります。
Excelのソルバー機能であれば初期値と変数の範囲を正確に指定すれば解くことができます。ただし、かなり収束しづらいです。
今回はPythonを使用して13変数のNewton-Raphson法で解いてみます。
ライブラリ・モジュールのインポート
行列式を利用するのでNumpyをインポートします。
また、自動で微分してヤコビ行列を求めるためにautogradというモジュールをインポートします。
#モジュールインポート
import autograd.numpy as np
from autograd import jacobian連立方程式の入力
立式した13個の方程式を入力します。
#連立方程式
#x[0]=x1
#x[1]=x2
#x[2]=y1
#x[3]=y2
#x[4]=z1
#x[5]=z2
#x[6]=F
#x[7]=D
#x[8]=W
#x[9]=P10
#x[10]=P20
#x[11]=P
#x[12]=T
func1=lambda x: x[6]-100
func2=lambda x: x[4]-0.2
func3=lambda x: x[11]-101300
func4=lambda x: x[7]-80
func5=lambda x: x[0]+x[1]-1
func6=lambda x: x[2]+x[3]-1
func7=lambda x: x[4]+x[5]-1
func8=lambda x: x[6]*x[4]-x[7]*x[2]-x[8]*x[0]
func9=lambda x: x[6]*x[5]-x[7]*x[3]-x[8]*x[1]
func10=lambda x: x[11]*x[2]-x[9]*x[0]
func11=lambda x: x[11]*x[3]-x[10]*x[1]
func12=lambda x: np.log(x[9])-20.7936+2788.51/(x[12]-52.36)
func13=lambda x: np.log(x[10])-20.9065+3096.52/(x[12]-53.67)def文を使用して方程式を定義してもよいのですが、行数が多くなってしまいます。
そこでlambda式を使用することで1行で簡潔に記述することができます。
また、def文やlambda式で記述するときは方程式をイコールゼロの形にしなければなりません。
今回は左辺-右辺=0の形にして記述しました。
加えて def文やlambda式で連立方程式を定義する際に、変数をx、y、z・・・という複数のアルファベットで定義してしまうとうまく連立計算できない事象が発生します。
私が無知なだけでうまく変数を定義するやり方もあるかもしれません。
代替案として、変数をx[0]、x[1]、x[2]として記述してx[0]=x1、x[1]=x2と割り当てる手法でうまく計算できます。
ここでは
- x[0]=x1
- x[1]=x2
- x[2]=y1
- x[3]=y2
- x[4]=z1
- x[5]=z2
- x[6]=F
- x[7]=D
- x[8]=W
- x[9]=P10
- x[10]=P20
- x[11]=P
- x[12]=T
以上のように変数を割り当てました。Pythonでは数字は0からカウントされるので、x[0]~x[12]までで13変数です。
ヤコビ行列の入力
次にNewton-Raphson法の計算に必要なヤコビ行列の要素を入力しています。
#ヤコビ行列
jac_func1=jacobian(func1)
jac_func2=jacobian(func2)
jac_func3=jacobian(func3)
jac_func4=jacobian(func4)
jac_func5=jacobian(func5)
jac_func6=jacobian(func6)
jac_func7=jacobian(func7)
jac_func8=jacobian(func8)
jac_func9=jacobian(func9)
jac_func10=jacobian(func10)
jac_func11=jacobian(func11)
jac_func12=jacobian(func12)
jac_func13=jacobian(func13)autogradのjacobian関数を使用することで各式を全微分しています。
これらの式は後の記述で行列式とします。
その他計算条件の入力
主にNewton-Raphson法の収束計算に必要な条件を入力しています。
#その他計算条件
i=0 #繰り返し計算回数
error=100 #誤差初期値
tol=10.**(-5) #許容誤差
maxiter=100 #最大繰り返し計算回数
M=13 #行列サイズ指定
N=13 #行列サイズ指定特に今回は行列サイズを指定して記述しています。行列サイズを指定しないとエラーになることが多い気がします。
初期値の入力
Newton-Raphson法には初期値が必要ですので入力します。
初期値
x_0=np.array([0.5,0.5,0.5,0.5,0.2,0.8,100,80,20,100000,100000,101300,150],dtype=float).reshape(N,1)np.arrayの括弧内は左から順に(x[0],x[1],・・・x[12])の初期値となっています。
できる限り解に近い初期値を入力することが望ましいです。今回は計算条件から簡単に値がわかるものは初期値として利用しています。(z1=0.2、z2=0.8など)
少なくとも初期値には取りえる可能性のある値をいれましょう。例えばx1、x2のような組成なのに1以上の値を入れると収束しづらくなります。
多変数Newton-Raphson法の入力
メインのNewton-Raphson法を入力しています。
#多変数Newton-Raphson法
while np.any(abs(error)>tol) and i < maxiter:
fun_evaluate=np.array([func1(x_0),
func2(x_0),
func3(x_0),
func4(x_0),
func5(x_0),
func6(x_0),
func7(x_0),
func8(x_0),
func9(x_0),
func10(x_0),
func11(x_0),
func12(x_0),
func13(x_0)]).reshape(M,1)
jac=np.array([jac_func1(x_0),
jac_func2(x_0),
jac_func3(x_0),
jac_func4(x_0),
jac_func5(x_0),
jac_func6(x_0),
jac_func7(x_0),
jac_func8(x_0),
jac_func9(x_0),
jac_func10(x_0),
jac_func11(x_0),
jac_func12(x_0),
jac_func13(x_0)])
jac=jac.reshape(N,M)
x_new=x_0-np.linalg.pinv(jac)@fun_evaluate
error=x_new-x_0
x_0=x_new
print(i)
print(error)
i=i+12行目でwhile文により繰り返し計算条件を入力しています。今回は条件を2つ入力しています。
まずany関数を使用して繰り返し計算の許容誤差に関する設定を行なっています。any関数は括弧内の条件を満たせばTrueを返す関数です。したがって、許容誤差よりも繰り返し計算のerror値の方が大きければTrueを返します。
次に繰り返し計算回数iが最大繰り返し計算回数より小さいことを条件として入力しています。
まとめると、繰り返し計算のerror値が十分に小さくなり許容誤差より小さくなるか、最大繰り返し計算回数に達するとwhile文がFalseとなり繰り返し計算が終了します。
3~15行目で(6)式の
\begin{pmatrix}-f(x_{i},y_{i})\\-g(x_{i},y_{i})\end{pmatrix}
の部分の行列を入力しています。
17~29行目でヤコビ行列の要素を入力しています。
30行目で定義したjacをN×M行列に変換しています。N=M=13なので13×13のヤコビ行列ができました。
32行目でNewton-Raphson法のメインの計算式を入力しています。
33行目で繰り返し計算の誤差であるerror値の計算をしています。
34行目で解の更新、35,36行目で繰り返し計算回数iとerror値の出力をしています。
出力
print関数を使用して以下のように出力します。
#出力
print("The solution is")
print(x_new)計算結果の確認
特に入力ミス等がなければ以下のように結果が表示されます。
0
[[-4.43893659e-01]
[ 4.43893659e-01]
[-2.64026585e-01]
[ 2.64026585e-01]
[-5.21166443e-13]
[-4.75175455e-14]
[-1.32871492e-11]
[ 8.52651283e-14]
[-2.22364349e-11]
[ 3.65869456e+04]
[-3.39869456e+04]
[ 1.45519152e-11]
[ 6.71613879e+01]]
1
[[ 7.86377890e-02]
[-7.86377890e-02]
[-1.96594472e-02]
[ 1.96594472e-02]
[ 1.61548552e-12]
[-4.99267294e-13]
[ 1.01607611e-11]
[-6.39488462e-13]
[ 1.15569776e-11]
[ 6.25297550e+04]
[ 2.35929250e+04]
[-1.45519152e-11]
[ 8.19052547e+01]]
2
[[-2.77865126e-02]
[ 2.77865126e-02]
[ 6.94662814e-03]
[-6.94662814e-03]
[-1.10891851e-12]
[ 5.71098724e-13]
[ 4.05009359e-12]
[ 7.10542736e-13]
[ 8.37019343e-12]
[ 9.79078239e+03]
[-1.54663573e+03]
[ 0.00000000e+00]
[ 6.02452893e+01]]
3
[[ 6.10765510e-04]
[-6.10765510e-04]
[-1.52691377e-04]
[ 1.52691377e-04]
[ 6.99440506e-15]
[-1.72084569e-14]
[-9.09494702e-13]
[-1.27897692e-13]
[ 1.69819714e-12]
[ 1.20599709e+03]
[ 1.25668011e+02]
[ 0.00000000e+00]
[ 1.84598750e+01]]
4
[[-1.61938735e-05]
[ 1.61938736e-05]
[ 4.04846840e-06]
[-4.04846841e-06]
[ 7.63278329e-15]
[-7.10542736e-15]
[-1.42108547e-14]
[-2.84217094e-14]
[ 6.07514039e-13]
[ 2.85965026e+01]
[-1.97372332e+00]
[ 0.00000000e+00]
[ 1.18146651e+00]]
5
[[-3.80530639e-08]
[ 3.80530639e-08]
[ 9.51326593e-09]
[-9.51326617e-09]
[-2.77555756e-17]
[ 0.00000000e+00]
[ 0.00000000e+00]
[ 0.00000000e+00]
[ 1.42108547e-14]
[ 8.76163650e-02]
[-4.80405279e-03]
[ 0.00000000e+00]
[ 4.32069615e-03]]
6
[[-5.09273179e-13]
[ 5.09259301e-13]
[ 1.27287070e-13]
[-1.27231559e-13]
[ 0.00000000e+00]
[ 0.00000000e+00]
[ 0.00000000e+00]
[ 0.00000000e+00]
[-1.42108547e-14]
[ 1.14590512e-06]
[-6.45668479e-08]
[ 0.00000000e+00]
[ 5.73670036e-08]]
The solution is
[[1.07552151e-01]
[8.92447849e-01]
[2.23111962e-01]
[7.76888038e-01]
[2.00000000e-01]
[8.00000000e-01]
[1.00000000e+02]
[8.00000000e+01]
[2.00000000e+01]
[2.10142164e+05]
[8.81830331e+04]
[1.01300000e+05]
[3.78957594e+02]]各計算ステップでのx[0]~x[12]の誤差が表示されています。6回目の計算で全ての変数の誤差が設定した10-5を下回ったので収束したことがわかります。
最終的な解はThe solution isの下に表示されています。
- x1=0.108
- x2=0.892
- y1=0.223
- y2=0.777
- z1=0.2
- z2=0.8
- F=100
- D=80
- W=20
- P10=210,142
- P20=88,183
- P=101,300
- T=379
となりました。
全体のコードを下に載せておきます。
#モジュールインポート
import autograd.numpy as np
from autograd import jacobian
#連立方程式
#x[0]=x1
#x[1]=x2
#x[2]=y1
#x[3]=y2
#x[4]=z1
#x[5]=z2
#x[6]=F
#x[7]=D
#x[8]=W
#x[9]=P10
#x[10]=P20
#x[11]=P
#x[12]=T
func1=lambda x: x[6]-100
func2=lambda x: x[4]-0.2
func3=lambda x: x[11]-101300
func4=lambda x: x[7]-80
func5=lambda x: x[0]+x[1]-1
func6=lambda x: x[2]+x[3]-1
func7=lambda x: x[4]+x[5]-1
func8=lambda x: x[6]*x[4]-x[7]*x[2]-x[8]*x[0]
func9=lambda x: x[6]*x[5]-x[7]*x[3]-x[8]*x[1]
func10=lambda x: x[11]*x[2]-x[9]*x[0]
func11=lambda x: x[11]*x[3]-x[10]*x[1]
func12=lambda x: np.log(x[9])-20.7936+2788.51/(x[12]-52.36)
func13=lambda x: np.log(x[10])-20.9065+3096.52/(x[12]-53.67)
#ヤコビ行列
jac_func1=jacobian(func1)
jac_func2=jacobian(func2)
jac_func3=jacobian(func3)
jac_func4=jacobian(func4)
jac_func5=jacobian(func5)
jac_func6=jacobian(func6)
jac_func7=jacobian(func7)
jac_func8=jacobian(func8)
jac_func9=jacobian(func9)
jac_func10=jacobian(func10)
jac_func11=jacobian(func11)
jac_func12=jacobian(func12)
jac_func13=jacobian(func13)
#その他計算条件
i=0 #繰り返し計算回数
error=100 #誤差初期値
tol=10.**(-5) #許容誤差
maxiter=100 #最大繰り返し計算回数
M=13 #行列サイズ指定
N=13 #行列サイズ指定
#初期値
x_0=np.array([0.5,0.5,0.5,0.5,0.2,0.8,100,80,20,100000,100000,101300,150],dtype=float).reshape(N,1)
#多変数Newton-Raphson法
while np.any(abs(error)>tol) and i < maxiter:
fun_evaluate=np.array([func1(x_0),
func2(x_0),
func3(x_0),
func4(x_0),
func5(x_0),
func6(x_0),
func7(x_0),
func8(x_0),
func9(x_0),
func10(x_0),
func11(x_0),
func12(x_0),
func13(x_0)]).reshape(M,1)
jac=np.array([jac_func1(x_0),
jac_func2(x_0),
jac_func3(x_0),
jac_func4(x_0),
jac_func5(x_0),
jac_func6(x_0),
jac_func7(x_0),
jac_func8(x_0),
jac_func9(x_0),
jac_func10(x_0),
jac_func11(x_0),
jac_func12(x_0),
jac_func13(x_0)])
jac=jac.reshape(N,M)
x_new=x_0-np.linalg.pinv(jac)@fun_evaluate
error=x_new-x_0
x_0=x_new
print(i)
print(error)
i=i+1
#出力
print("The solution is")
print(x_new)Scipyによる計算
Scipyのoptimize.root関数を使用すればより簡単に非線形方程式を解くことができます。
#モジュールインポート
import scipy.optimize as scopt
#連立方程式定義
def func(x):
return [x[6]-100,
x[4]-0.2,
x[11]-101300,
x[7]-80,
x[0]+x[1]-1,
x[2]+x[3]-1,
x[4]+x[5]-1,
x[6]*x[4]-x[7]*x[2]-x[8]*x[0],
x[6]*x[5]-x[7]*x[3]-x[8]*x[1],
x[11]*x[2]-x[9]*x[0],
x[11]*x[3]-x[10]*x[1],
np.log(x[9])-20.7936+2788.51/(x[12]-52.36),
np.log(x[10])-20.9065+3096.52/(x[12]-53.67)]
x0=[0.5,0.5,0.5,0.5,0.2,0.8,100,80,20,100000,100000,101300,150]
#Scipy関数
xnew=scopt.root(func,x0)
#出力
print(xnew)上のコードで計算させると、下のように計算が成功したと表示されます。
success: True
x: array([1.07552151e-01, 8.92447849e-01, 2.23111962e-01, 7.76888038e-01,
2.00000000e-01, 8.00000000e-01, 1.00000000e+02, 8.00000000e+01,
2.00000000e+01, 2.10142164e+05, 8.81830331e+04, 1.01300000e+05,
3.78957594e+02])自分でNewton-Raphson法のコードを書いて計算した結果と全く同じになりました。
このようにoptimize.root関数を使用すれば連立非線形方程式でも簡単に解くことができます。
ただし、変数が多くなると解が収束しづらくなる傾向があるようです。試しに100変数程度の計算をしてみたら収束しませんでした。
化学工学の実務では数百~数千変数の計算をしますから、optimize.root関数をそのまま使用して楽することはできないようです。計算の順序を工夫してより収束しやすいアルゴリズムを考える必要があります。
まとめ
多変数のNewton-Raphson法について解説しました。
商用の化工シミュレータでも使用される手法なので必ず理解しておきたいところです。


