概要
蒸留操作や吸収操作で棚段塔を使用する場合を考えます。
理想的な条件を考えると、トレイの各段では気液平衡に達しています。
このときに、要求される塔出口のスペックを満たすために必要なトレイ段数のことを理論段数といいます。
実際にはトレイ上の気液は平衡状態に達していないため、理想的な条件と比べると棚段塔の性能は低くなっています。
したがってトレイの実段数は理論段数よりも多くして、確実に所定の出口スペックを満たすように設計するのが普通です。
理論段数の推算方法
実務で使用する化工シミュレータでは理論段数はユーザーが指定する入力値となります。
何も情報がないと当てずっぽうで理論段数を入力しがちですが、これは本来良くありません。
下で紹介するような方法で簡易的にでもよいので理論段数のあたりをつけておくと、シミュレータで試行錯誤する回数が減り時間短縮になります。
McCabe-Thieleの階段作図
最も簡便に理論段数を求める方法です。
2成分系でラウールの法則が成り立つ理想溶液に近い系であれば、比較的精度良く計算できます。
-

【McCabe-Thieleの階段作図】を徹底解説:蒸留塔理論段数の簡易計算法
理論段数を作図で簡便に求める方法のことを、McCabe-Thiele(マッケーブ-シール)の階段作図といいます。この方法は蒸留塔の操作を図で表すことで、蒸留操作を直感的に理解できる点が非常に優れています。
続きを見る
Fenskeの式(最小理論段数)
同様に理想溶液に近い場合に成り立つ式です。
$$N_{m}=\frac{{\rm{log}}(\frac{x_{D}}{1-x_{D}})(\frac{1-x_{W}}{x_{W}})}{{\rm{log}}α}-1$$
Nm:最小理論段数、α:相対揮発度
xD:低沸分の留出組成、xw:低沸分の缶出組成
全還流のときの理論段数、つまり最小理論段数を算出することができます。
最小理論段数は次に紹介するGillilandの相関で理論段数を算出するのに使用します。
Gillilandの相関(必要理論段数)
縦軸に(N-Nm)/(N+2)、横軸に(R-Rm)/(R+1)をプロットしたグラフを下に示します。
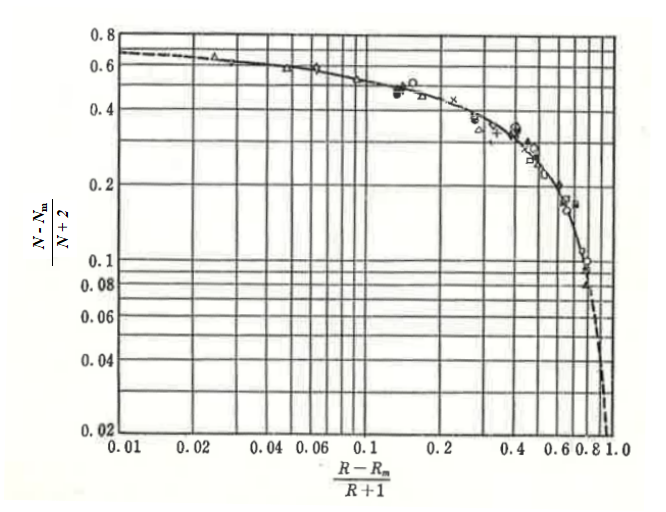
N:理論段数、Nm:最小理論段数
R:還流比、Rm:最小還流比
横軸の値を計算しこのグラフから縦軸の値を読み取ることで、理論段数を計算できます。
また、後に平田氏がGillilandの相関を片対数を取ることで線形的な式にしました。
$${\rm{log}}\frac{N-N_{m}}{N+2}=-0.9(\frac{R-R_{m}}{R+1})-0.17$$
上式の適用範囲は、(R-Rm)/(R+1)<0.7です。
この式はメタノール-水系のような非理想系にもよく合うと言われています。
