概要
Newton-Raphson法(単にNewton法ともいいます)は非線型方程式を解く手法の中でもかなり有名です。
Excelのゴールシーク機能のアルゴリズムがNewton-Raphson法、もしくはその改良版だと言われていますし、その他の数値計算ソフトでもNewton-Raphson法が採用されている例は多いです。
Newton-Raphson法はある関数f(x)について、f(x)=0となるような解xを繰り返し計算で求める手法です。
f(x)=0が解析的に計算できる場合にはわざわざこの手法を使用する必要はないかもしれません。
ただし、関数f(x)に指数や対数が含まれていて非線形となっていると、解析的に解くことができません。
そのような場合に、このNewton-Raphson法は役に立ちます。
本記事ではNewton-Raphson法の計算手法の解説及び、実際にExcelを使用して例題を解いています。化学工学では非線形方程式の解を求める機会が多いと思いますので、ご参考になれば幸いです。
Newton-Raphson法の計算手法
原理
関数f(x)=0の解を求めてみましょう。
Newton-Raphson法はある値x0において、関数f(x)の接線のx切片の値が元のx0の値より真の解に近くなることを利用しています。
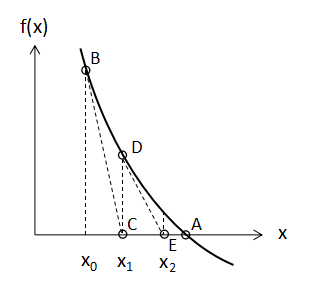
字面だけだとわかりづらいので上に図を示します。
求めたいのはf(x)=0となる点Aの値です。
ある初期値x=x0の点Bから接線を引き、x=0と交わる点をCとします。
点Cにおける値x1はもとのx0よりも点Aに近い値となっていますね。
あとは同様にx=x1となる点Dで接線を引き、x切片である点Eを算出する・・・という操作を繰り返していけば、いずれは点Aとほとんど変わらない値を得ることができます。
これらの操作がNewton-Raphson法の原理です。
計算式
収束計算式
関数f(x)を初期値x0の近傍x0+ΔxでTaylor展開します。
$$f(x_{0}+Δx)=f(x_{0})+\frac{Δx}{1!}f'(x_{0})+\frac{Δx^{2}}{2!}f''(x_{0})+・・・=0 ・・・(1)$$
(1)式の2次以上の項は微小であり無視できますので、
$$f(x_{0})+\frac{Δx}{1!}f'(x_{0})=0$$
$$Δx=-\frac{f(x_{0})}{f'(x_{0})}・・・(2)$$
Δxは(2)式で表すことができます。
したがってx1は
$$x_{1}=x_{0}+Δx=x_{0}-\frac{f(x_{0})}{f'(x_{0})}・・・(3)$$
(3)式となります。
この操作をn回繰り返すと、
$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}・・・(4)$$
(4)式となり、Newton-Raphson法を任意の回数繰り返すことができます。
収束判定
(4)式をx0,x1,x2・・・と繰り返すことでf(x)=0の解に収束していきますが、やろうと思えば何回でも繰り返すことができます。
そのため、どこかで計算を打ち切る必要があります。
通常は何回目かの計算でほとんどxの値が変わらなくなってくるので、そのタイミングで打ち切るのが望ましいです。
定量的には、計算誤差δが
$$\left| x_{n+1}-x_{n}\right|<δ・・・(5)$$
(5)式を満たせば計算が収束したとみなせます。
δの値は十分小さければなんでもよいのですが、計算する式の分野や背景によって許容される誤差は変わってくると思います。
化学工学ではδ=10-4程度で設定すれば十分な精度でしょう。
初期値に関する注意点
Newton-Raphson法を使用するときの注意点は、初期値x0をなるべく解に近い値で設定することです。
もし解とは全く異なる値を初期値として設定してしまうと、計算が収束しなかったり、あるいはf(x)=0の解が複数ある場合は異なる解に収束する可能性があります。
例えば上図のようにf(x)=0の解が2つある場合を考えます。
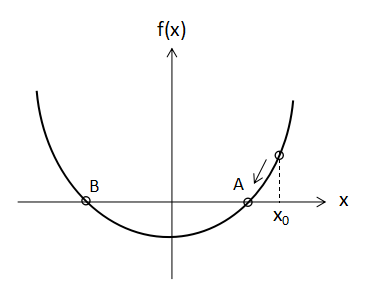
ほしい解が点Aの解だとすると、初期値x0は正の値でなるべく点Aに近い値を予想して入力する必要があります。
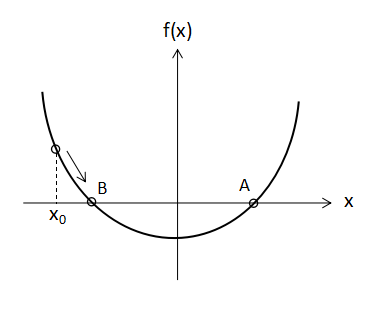
もし初期値x0を負の値にしてしまうと点Bの方に計算が収束する可能性があります。
点Bの値でもf(x)=0の解ではあるのだから、別にこちらに収束してもよいのではないかと思われるかもしれませんが、それはあくまでも数学の考え方です。
私たちが普段計算している化学工学では、流量、温度、圧力、濃度等のパラメータを扱いますが、これらは基本的に正の値です。
(温度、圧力は負の値で表す方法もありますが、この手の化学工学計算では温度は℃ではなくKで、圧力はゲージ圧ではなく絶対圧で計算するのが普通です。)
そのため負の値で解が収束した場合には、基本的に間違った計算をしていると判断すべきです。
加えて、計算しているパラメータが常識的に取りうる値の範囲というのも決まっていますから、それを考慮したうえで初期値を設定すべきです。
例えば流量は前後の物質収支の関係から取りうる値が制限されますし、濃度はかならず0~100%の間の値を取ります。
優秀なケミカルエンジニアほど初期値の設定が上手だと思います。
例題:対数平均温度差の伝熱計算
計算条件
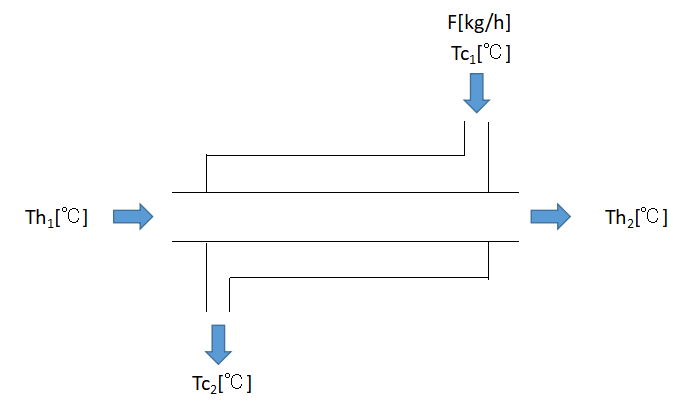
例題では上図に示すような熱交換器の伝熱計算をやってみます。
以下の条件がわかっているものとします。
- 低温側流体流量F:45,000kg/h
- 低温側流体比熱Cp:1.0kcal/(kg・℃)
- 熱交換器の総括伝熱係数U:550kcal/(m2・h・℃)
- 熱交換器の伝熱面積A:20m2
- 高温側流体の入口温度Th1:78℃
- 低温側流体の入口温度Tc1:31℃
- 低温側流体の出口温度Tc2:38℃
以上の条件から、高温側流体の出口温度Th2を求めます。
基礎式の導出
まずは、低温側流体の流量や入出口の温度から交換熱量Qについて式を立てると、
$$Q=FCp(Tc2-Tc1)・・・(6)$$
(6)式のようになります。
続いて熱交換器の総括伝熱係数Uや伝熱面積から、同じく交換熱量Qについて式を立てます。
$$Q=UAΔT_{lm}=UA\frac{(Th1-Tc2)-(Th2-Tc1)}{{\rm{ln}}(\frac{Th1-Tc2}{Th2-Tc1})}・・・(7)$$
(6)式と(7)式の交換熱量Qは等しくなりますから、
$$FCp(Tc2-Tc1)=UA\frac{(Th1-Tc2)-(Th2-Tc1)}{{\rm{ln}}(\frac{Th1-Tc2}{Th2-Tc1})}$$
となります。
この式が式変形のみで解析的に解ける場合はわざわざNewton-Raphson法を使う必要はないかもしれません。
今回は対数項が含まれており、Th2について解くのは困難ですね。
このような場合は方程式を近似的に解く必要があり、その手法の1つとしてNewton-Raphson法は非常に有効です。
Newton-Raphson法の適用
Newton-Raphson法を適用するために、f(Th2)=左辺-右辺=0の形にすると、
$$f(Th2)=FCp(Tc2-Tc1)-UA\frac{(Th1-Tc2)-(Th2-Tc1)}{{\rm{ln}}(\frac{Th1-Tc2}{Th2-Tc1})}・・・(8)$$
(8)式となります。
この(8)式を温度Th2の関数としてf(Th2)=0となるTh2を算出します。
今回はExcelに式を入力して計算しました。
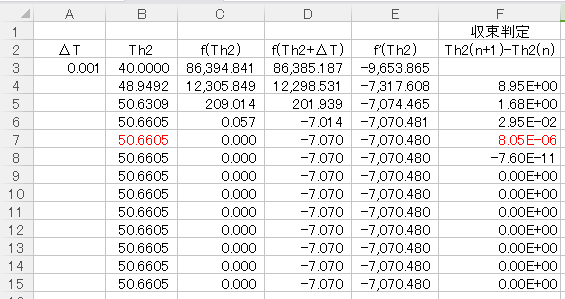
まず初期値を適当に決定します。
78℃で流入する高温流体を31~38℃の低温流体で冷却するわけですから、高温側の出口温度Th2の解は38~78℃の間にありそうだということがわかります。
加えて熱交換器の設計面で考えると、高温側と低温側の温度差ΔTlmが小さくなると効率が悪くなります。
したがって、高温側の出口温度Th2が低温流体の温度38℃に近い温度まで冷えるような設計にすることはほとんどないでしょう。仮に40℃以下まで冷却したければ他のもっと温度の低い冷媒を使うべきです。
よって、現実的には高温側の出口温度Th2は45~70℃くらいの範囲に入ることが多いと思います。
このように化学工学の知識や装置設計の知見を活かしてなるべく妥当な初期値を決めましょう。
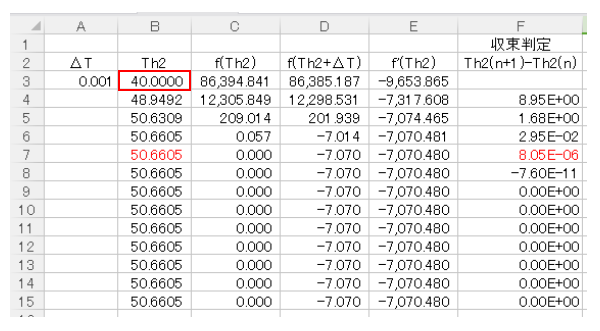
今回は例題ということで、あまりに早く収束するとやりがいがないので初期値は40℃とし、上図のB3セルに入力します。
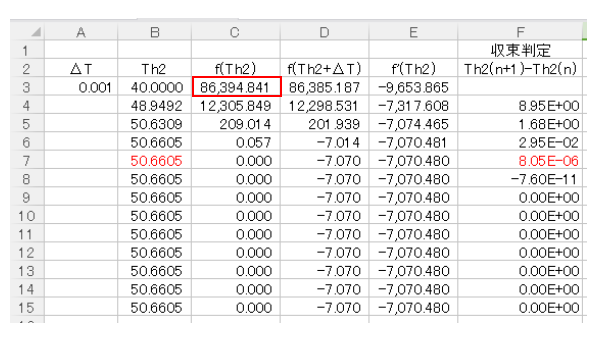
続いて(8)式から関数f(Th2)をC3セルに入力します。流量や比熱等の変化しない値は他のセルに入力し、$を付けて固定しておくとよいでしょう。
変数Th2はB3セルを選択しておきます。
続いてf'(Th2)を算出します。
本来は(8)式の関数f(Th2)を微分してf'(Th2)を算出するのがよいと思います。ただ今回は対数平均温度差の項が複雑で、微分するのが難しい、あるいは面倒くさいですね。
そこで少し工夫をします。要は初期値f(Th2(0))での接線の傾きf'(Th2(1))が算出できればよいのです。
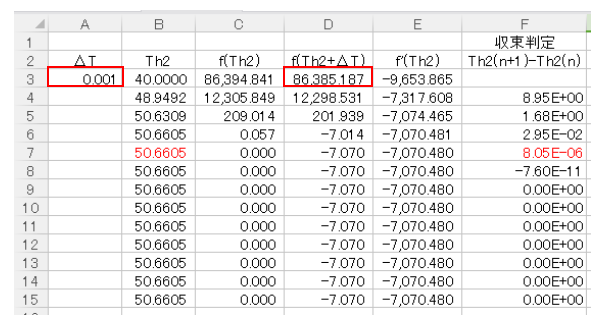
初期値Th2(0)から微小な温度ΔTだけ変化した点f(Th2(0)+ΔT)の値をD3セルに入力します。
ΔTの刻みは十分小さければなんでもよいです。今回はΔT=0.001とし、A3セルに入力しておきます。
これらの値からf'(Th2(1))は、
$$f'(Th2(1))=\frac{f(Th2(0)+ΔT)-f(Th2(0))}{ΔT}・・・(9)$$
(9)式で表すことができます。

この式をE3セルに入力します。
ΔTは変化しないため$で固定しておくとよいでしょう。
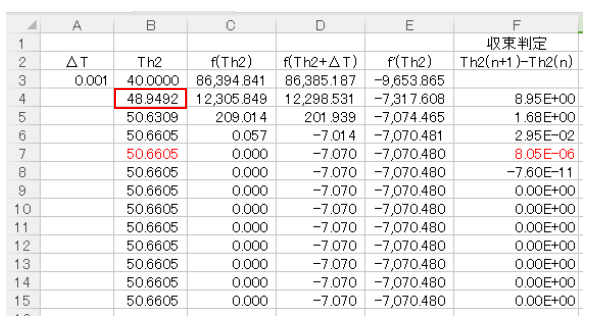
続いてB4セルに(4)式を入力します。
$$B4セル=B3セル-\frac{C3セル}{E3セル}・・・(10)$$
B4セルは(10)式のような参照セルになります。
これでNewton-Raphson法の1回目の計算が終了し、Th2(1)=48.9492℃となりました。
B4セルの計算結果が出れば、収束判定をしましょう。

F4セルにTh2(n+1)-Th2(n)の値を入力します。F4セルは
$$F4セル=B4セル-B3セル=48.9492-40.0000=8.95E+00$$
となっています。収束判定値δ=10-4よりも大きな値なので、収束していないと判断し繰り返し計算を続行します。
あとは同様の計算を繰り返すだけです。
計算の結果、
Th2(2)=50.6309℃
Th2(3)=50.6605℃
Th2(4)=50.6605℃
・・・
となり、Th2(3)以降は値が変わらなくなりました。
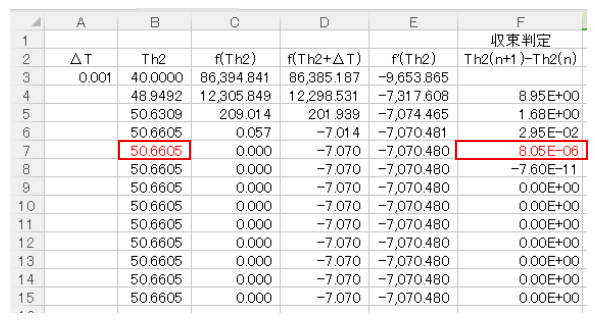
収束判定をみると、Th2(4)の計算終了時の判定値が8.05E-06で10-4よりも小さい値となっています。
したがって、今回のNewton-Raphson法は4回の繰り返しで収束しました。
f(Th2)=0の近似解は50.6605℃となりました。
汎用シミュレータやプログラミング言語の利用
ちなみに、今回の例題程度の簡単な計算であれば、Excelのゴールシークやソルバー機能を使用すると自分でRewton-Raphson法の計算式を書かなくても似たような計算をしてくれます。
非常に便利ですね。
ただし、実務ではこの例題のような方程式をいくつも連立させて解くことが多く、その場合にはExcelのゴールシークやソルバーでは収束しないことが多いです。
そのため、Aspen Plusのような汎用の化工計算シミュレータを利用したり、VBAやFortran、Pythonといった自分で計算プログラムを書いて計算する手法を取ります。
弊社ではAspen Plusで化工計算をする人がほとんどですが、汎用シミュレータに慣れてしまうと収束計算のメカニズムを勉強しなくなるのがデメリットだと思います。
そのソフトが使用できない環境に移ってしまうと今までできていた化工計算ができなくなるため、本当の意味で実力が付いたとは言えません。
また、汎用シミュレータも万能ではなく、非理想性の高い系やリサイクルが多い系では収束しないことがよくあります。
したがって、どのようなアルゴリズムが収束計算に使用されており、どう設定すれば収束しやすくなるかを勉強することは非常に重要です。
まとめ
非線形方程式の代表的な解法の1つであるNewton-Raphson法について解説しました。
この手法では解に近いところで初期値を取り、(4)式で繰り返し計算をすることでf(x)=0の解を得ることができます。
