概要
熱交換器等の交換熱量の計算にあたって温度差を求める必要がありますが、装置内で流体が伝熱により温度変化し、入口と出口で温度が異なる場合はどの区間で温度差を取るべきか判断が難しいです。
そこで高温流体、低温流体の入口、出口の温度からその装置の温度差を代表的に計算した値を交換熱量の計算に使用します。この温度差のことを対数平均温度差ΔTlmといいます。
英語ではLogarithmic Mean Temperature Differenceといい、頭文字を取ってLMTDと表されます。
一般に高温流体と低温流体がワンパスで向流接触する伝熱における対数平均温度差は
$$ΔT_{lm}=\frac{(T_{h1}-T_{c2})-(T_{h2}-T_{c1})}{{\rm{ln}}[\frac{(T_{h1}-T_{c2})}{(T_{h2}-T_{c1})}]}$$
Th1:高温流体の入口温度、Th2:高温流体の出口温度
Tc1:低温流体の入口温度、Tc2:低温流体の出口温度
上式で表されます。
対数平均温度差の導出
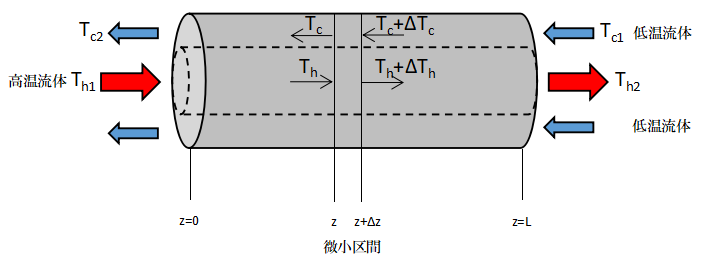
上図のような二重管で高温流体と低温流体がワンパスで向流接触する伝熱を考えます。
化学工学系の式の導出でありがちなのが、最初は微小区間について収支式を取り、後で積分して系全体の収支を出すというやり方です。
対数平均温度差もそのやり方で導出していきます。
長さLの伝熱管において任意の微小区間Δz(z=z~z+Δz)について高温流体と低温流体それぞれの熱収支を取ります。
高温流体はこの微小区間でΔThだけ温度変化すると考えると
$$ΔQ=-W_{h}C_{ph}ΔT_{h}・・・(1)$$
ΔQ:微小区間における交換熱量[W]、Wh:高温流体の質量流量[kg/s]
Cph:高温流体の比熱[J/(kg K)]
となります。
高温流体はThからTh+ΔThへ温度が下がりΔTh<0となるため、右辺にマイナスをつけてΔQをプラスの値に調整します。
質量流量や比熱はこの後の導出仮定で消えてなくなるのでどんな値や単位をとってもかまいません。
低温流体も同様に微小区間でΔTcだけ温度変化すると考えると
$$ΔQ=-W_{c}C_{pc}ΔT_{c}・・・(2)$$
ΔQ:微小区間における交換熱量[W]、Wc:低温流体の質量流量[kg/s]
Cpc:低温流体の比熱[J/(kg K)]
となります。
低温流体はTc+ΔTcからTcへ温度が上がりΔTc<0となるためこちらも右辺にマイナスをつけてΔQをプラスの値に調整します。
次にz=zでの高温流体から低温流体への伝熱を考えます。
総括伝熱係数をUo(外径基準)とするとQ=UAΔTの関係から
$$ΔQ=U_{o}πD_{o}Δz(T_{h}-T{c})・・・(3)$$
ΔQ:微小区間における交換熱量[W]、Do:伝熱管外径[m]
Th:z=zにおける高温流体の温度[K]、Tc:z=zにおける低温流体の温度[K]
となります。
ここでは外径基準で収支式を立てていますが、内径基準で式を立ててもかまいません。
(1)式=(3)式
(2)式=(3)式
としてΔQを消去します。左辺に温度を集めて整理すると、
$$\frac{ΔT_{h}}{T_{h}-T{c}}=-\frac{U_{o}πD_{o}Δz}{W_{h}C_{ph}}・・・(4)$$
$$\frac{ΔT_{c}}{T_{h}-T{c}}=-\frac{U_{o}πD_{o}Δz}{W_{c}C_{pc}}・・・(5)$$
となります。
ここで(4)式から(5)式を引くと
$$\frac{Δ(T_{h}-T_{c})}{T_{h}-T_{c}}=-U_{o}πD_{o}Δz(\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}})$$
Δz→0とすると微分系になり
$$\frac{d(T_{h}-T_{c})}{T_{h}-T_{c}}=-U_{o}πD_{o}(\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}})dz・・・(6)$$
となります。
(6)式を温度差についてTh1-Tc2~Th2-Tc1、伝熱管長さについて0~Lまで積分します。
$$\int_{T_{h1}-T_{c2}}^{T_{h2}-T_{c1}}\frac{d(T_{h}-T_{c})}{T_{h}-T_{c}}=-U_{o}πD_{o}(\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}})\int_{0}^{L}dz$$
$${\rm{ln}}\frac{T_{h1}-T_{c2}}{T_{h2}-T_{c1}}=U_{o}πD_{o}L(\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}})・・・(7)$$
となります。
次にz=0~Lの全区間で熱交換されるトータル交換熱量Qは高温流体側、低温流体側でそれぞれ
$$Q=W_{h}C_{ph}(T_{h1}-T_{h2})=W_{c}C_{pc}(T_{c2}-T_{c1})$$
となります。
ここでWhCph、WcCpcを抵抗の形で書き換えて加比の定理を使用します。
加比の定理について詳しく知りたい方は外部サイトを参照してください。
$$Q=\frac{(T_{h1}-T_{h2})}{\frac{1}{W_{h}C_{ph}}}=\frac{(T_{c2}-T_{c1})}{\frac{1}{W_{c}C_{pc}}}=\frac{(T_{h1}-T_{h2})-(T_{c2}-T_{c1})}{\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}}}$$
$$\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}}=\frac{(T_{h1}-T_{h2})-(T_{c2}-T_{c1})}{Q}$$
$$\frac{1}{W_{h}C_{ph}}-\frac{1}{W_{c}C_{pc}}=\frac{(T_{h1}-T_{c2})-(T_{h2}-T_{c1})}{Q}・・・(8)$$
となります。
最後に(8)式を(7)式に代入すれば
$$Q=U_{o}πD_{o}L\frac{(T_{h1}-T_{c2})-(T_{h2}-T_{c1})}{{\rm{ln}}[\frac{(T_{h1}-T_{c2})}{(T_{h2}-T_{c1})}]}$$
$$Q=U_{o}A_{o}ΔT_{lm}$$
となり、概要で説明した式になります。
