概要
本記事ではPythonでの化学工学計算例を紹介しています。今回はEuler法を使用して、タンク内の原料濃度変化を計算します。
バッチ反応器やセミバッチ反応器では原料濃度が変化するため、類似の計算をすることがあると思います。
実務では濃度変化の式と温度変化の式を連立させて解くなどの複雑な計算が多いですが、今回は濃度変化のみの基礎的な式で解いてみます。
基礎的な理論や計算手法をきちんと理解できれば、応用するのも簡単です。
計算式
今回計算する式は以下の記事で解説したものを使用します。
この記事ではExcelを使用してEuler法で解いていますが、今回は同じ式をPythonで解いてみます。
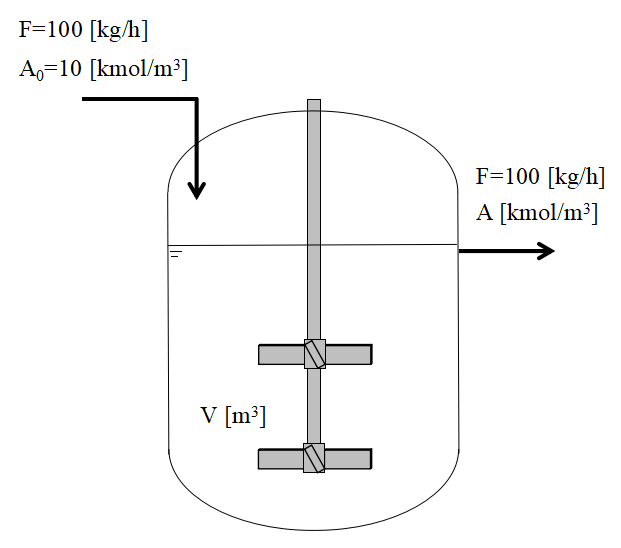
- 原料流量F:100kg/h
- タンク内の液量V:1.0m3
- 液体密度ρ:1000kg/m3
- 原料流入濃度A0:10kmol/m3
- タンク内の原料の初濃度:1kmol/m3
前提条件は以上の通りで、t=5.0h後のタンク内の原料濃度Aを求めます。
$$\frac{dA}{dt}=\frac{F}{ρV}(A_{0}-A)・・・(1)$$
計算式は(1)式で表され、Euler法で解いていきます。
ちゃんと計算できていれば、t=5.0hのときにA=4.55kmol/m3になるはずです。
Python記述
ライブラリ・モジュールのインポート
今回は特に入力する必要がないです。
ただ、毎回インポートの記述を変更するのが面倒くさければ、よく使うモジュールは消さずにそのままインポートしておいてよいかもしれません。
正しく記述できている分には計算に害はないでしょう。
前提条件の入力
問題で与えられる前提条件を入力します。
#前提条件
F=100 # kg/h
V=1 #m3
ρ=1000 #kg/m3
A0=10 #kmol/m3念のため単位を付けておくと後から見たときに単位変換ミスを防ぎやすくてよいです。
初期条件の入力
次に初期条件が必要な場合はその値を入力します。
今回は原料濃度の初期値と時間の初期値としてt=0を入力します。
#初期条件
A=1 #kmol/m3
t=0 # hその他計算条件の入力
今回は時間刻みΔtと繰り返し計算回数imaxを入力します。
#その他計算条件
dt=0.1 # h
imax=51 # 計算回数の指定時間刻みはΔt=0.1としました。
どのくらいの刻み幅が適切かは解く方程式や分野によるのでなんとも言えませんが、最初は粗めの刻み幅で計算し、誤差が大きそうであれば細かくするのが良いと思います。
最初から細かすぎる刻み幅で計算してしまうと、計算に時間がかかってしまいますので。
また、for文を使って繰り返し計算を行なう予定なので、繰り返し計算回数をimaxとして入力します。
imax=51としました。時間tを0.1h刻みで0.0~5.0hまで計算するので、繰り返し回数は51回となります。
方程式の定義
次にメインの方程式を定義します。
今回もdefとreturnで(1)式を定義します。
#方程式定義
def fA(A):
return F/(V*ρ)*(A0-A)(1)式の左辺dA/dt=fA(A)とし、右辺をreturnで計算値が返ってくるように入力します。
Euler法の入力
続いてEuler法を入力していきます。
今回はfor文を使用して繰り返し計算を入力します。
#Euler法
for i in range(imax):
print('i:{0:4}, t:{1:5.1f}, A:{2:6.2f}' .format(i,t,A))
A=A+dt*fA(A) #Euler法
t=t+dt #時間tの更新 2行目はfor文の文法にしたがって記入しています。繰り返し回数をiとおき、括弧内には繰り返し計算回数を入力します。
繰り返し計算回数は数字で入力してもいいですが、今回はその他計算条件でimaxと定義したのでそれを使用します。
3行目でfor文内の計算結果を各計算のステップごとに出力しています。出力にはprint関数を使用しています。
print関数の括弧内はどのような書式で出力するかを指定しています。
後ろに付いている.format(i,T,A)で計算回数i、時間t、原料濃度Aの3変数を出力すると指定し、前の' '内でそれぞれの変数の桁表示等を指定します。
最初の i : {0 : 4}についてですが、
- i : 計算出力画面にi : と表示されます。
- 0 formatの括弧内に入力した変数は順番に0,1,2と番号が自動的に振られているようで、計算回数iを出力したければ0を入力します。
- : 4 計算出力画面に表示される数字のマスと空白のマスの合計を意味します。自分で数字を適当にいじってみれば意味がよくわかると思います。出力画面の見栄えだけの問題なので特に指定しなくてもよいです。
次の t :{1 : 5 .1f}は、
- t: 計算出力画面にt: と表示されます。
- 1 時間tを出力したければ1を入力します。
- : 5 合計5マスで指定すれば見栄えがよい感じでした。
- .1f 小数点を何桁まで表示させるかを指定します。時間tは0.1h刻みなので小数点1桁で指定しました。
次の A :{2 : 6 .2f}は、
- A: 計算出力画面にA: と表示されます。
- 2 原料濃度Aを出力したければ2を入力します。
- : 6 合計6マスで指定すれば見栄えがよい感じでした。
- .2f 原料濃度は小数点2桁で指定しました。
以上でprint関数の設定は終了です。
また、今回1点工夫しているのはprint関数の入力位置です。
私が最初に参考にしたサイトだと、print関数をfor文の1番最後に入力していました。
もしprint関数を1番最後に入力すると、print関数で出力される前にt=t+dtが計算されてしまうため、最初に出力される値がt=0ではなくt=0.1となってしまいます。
計算自体はどちらの入力位置でも合っているのですが、流石に初期値は計算結果として出力してほしいですよね。
そのため、t=t+dtより前にprint関数を入力することで初期値t=0を出力できるようにしています。
次に5行目でEuler法の式を入力しています。こちらの記事で解説していますが、Euler法は以下の(2)式によって表されます。
$$A_{n+1}=A_{n}+Δt\frac{dA}{dt}・・・(2)$$
最後に6行目で時間tを更新します。
計算結果の出力
計算結果はfor文の中でprint関数によって出力されるため、特に個別で入力する必要はないです。
計算結果の確認
特に入力ミス等がなければ計算結果が以下のように表示されます。
i: 0, t: 0.0, A: 1.00
i: 1, t: 0.1, A: 1.09
i: 2, t: 0.2, A: 1.18
i: 3, t: 0.3, A: 1.27
i: 4, t: 0.4, A: 1.35
i: 5, t: 0.5, A: 1.44
i: 6, t: 0.6, A: 1.53
i: 7, t: 0.7, A: 1.61
i: 8, t: 0.8, A: 1.70
i: 9, t: 0.9, A: 1.78
i: 10, t: 1.0, A: 1.86
i: 11, t: 1.1, A: 1.94
i: 12, t: 1.2, A: 2.02
i: 13, t: 1.3, A: 2.10
i: 14, t: 1.4, A: 2.18
i: 15, t: 1.5, A: 2.26
i: 16, t: 1.6, A: 2.34
i: 17, t: 1.7, A: 2.41
i: 18, t: 1.8, A: 2.49
i: 19, t: 1.9, A: 2.56
i: 20, t: 2.0, A: 2.64
i: 21, t: 2.1, A: 2.71
i: 22, t: 2.2, A: 2.79
i: 23, t: 2.3, A: 2.86
i: 24, t: 2.4, A: 2.93
i: 25, t: 2.5, A: 3.00
i: 26, t: 2.6, A: 3.07
i: 27, t: 2.7, A: 3.14
i: 28, t: 2.8, A: 3.21
i: 29, t: 2.9, A: 3.28
i: 30, t: 3.0, A: 3.34
i: 31, t: 3.1, A: 3.41
i: 32, t: 3.2, A: 3.48
i: 33, t: 3.3, A: 3.54
i: 34, t: 3.4, A: 3.61
i: 35, t: 3.5, A: 3.67
i: 36, t: 3.6, A: 3.73
i: 37, t: 3.7, A: 3.79
i: 38, t: 3.8, A: 3.86
i: 39, t: 3.9, A: 3.92
i: 40, t: 4.0, A: 3.98
i: 41, t: 4.1, A: 4.04
i: 42, t: 4.2, A: 4.10
i: 43, t: 4.3, A: 4.16
i: 44, t: 4.4, A: 4.22
i: 45, t: 4.5, A: 4.27
i: 46, t: 4.6, A: 4.33
i: 47, t: 4.7, A: 4.39
i: 48, t: 4.8, A: 4.44
i: 49, t: 4.9, A: 4.50
i: 50, t: 5.0, A: 4.55時間t=5.0hのとき、原料濃度A=4.55kmol/m3となりましたね。
下に計算コードを最初から最後までまとめて載せておきます。
#前提条件
F=100 # kg/h
V=1 #m3
ρ=1000 #kg/m3
A0=10 #kmol/m3
#初期条件
A=1 #kmol/m3
t=0 # h
#その他計算条件
dt=0.1 # h
imax=51 # 計算回数の指定
#方程式定義
def fA(A):
return F/(V*ρ)*(A0-A)
#Euler法
for i in range(imax):
print('i:{0:4}, t:{1:5.1f}, A:{2:6.2f}' .format(i,t,A))
A=A+dt*fA(A) #Euler法
t=t+dt #時間tの更新 まとめ
Pythonでタンク内の原料濃度変化をEuler法で計算する方法を解説しました。
Euler法のような繰り返し計算ではfor文はよく使用すると思いますのでセットで覚えましょう。

