概要
本記事では連立一次方程式の計算として、逆行列を使用した解法を解説しています。
変数が2つ、3つの簡単な連立方程式ならば手計算で解くのが早い場合が多いですが、変数の数が増えるにしたがって式変形が複雑になりケアレスミスも起こりやすくなります。
特に計算ミスを防ぐ、という意味合いで手計算ではなく計算ソフトによる解法を知っておくことは意味があります。
今回はExcelとPythonの2つの計算手法で5元連立一次方程式を計算してみます。
計算の前提条件
$$C_{10}H_{20}+aO_{2}+bNH_{3} → cCH_{1.84}O_{0.41}N_{0.18}+dCO_{2}+eH_{2}O・・・(1)$$
前提条件として、
$$\frac{生成したCO_{2}のモル数}{消費されたO_{2}のモル数}=0.48・・・(2)$$
とします。
(1)式の各物質の係数a,b,c,d,eを決定します。(1)式はオレフィンを炭素源、アンモニアを窒素源として好気培養で微生物タンパクを生成する反応です。
パッと暗算で係数を決定できない程度には難しいですね。
計算式
連立方程式の作成
(1)式の各元素に注目して式を立てます。
$$炭素C:10=c+d・・・(3)$$
$$水素H:20+3b=1.84c+2e・・・(4)$$
$$酸素O:2a=0.41c+2d+e・・・(5)$$
$$窒素N:b=0.18c・・・(6)$$
次に(2)式の関係から、
$$d=0.48a・・・(7)$$
となります。
未知数5つに対して式が5つありますからこれで解くことができますね。
頑張って手計算で未知数を減らして解くこともできますが、それなりに面倒ですね。
今回は行列式を作成して解いてみましょう。
行列式の作成
(3)~(7)式を行列式に変換すると(8)式となります。
\(\begin{pmatrix}0&0&1&1&0\\0&-3&1.84&0&2\\-2&0&0.41&2&1\\0&-1&0.18&0&0\\0.48&0&0&-1&0\end{pmatrix}
\begin{pmatrix}a\\b\\c\\d\\e\end{pmatrix}
=\begin{pmatrix}10\\20\\0\\0\\0\end{pmatrix}\)
・・・(8)
(8)式はいわゆる
AX=B・・・(9)
(9)式のような形をしています。
(9)式にAの逆行列A-1をかければ、
X=A-1B・・・(10)
(10)式となり、求めたいXを算出することができます。
ここでは、
A=\(\begin{pmatrix}0&0&1&1&0\\0&-3&1.84&0&2\\-2&0&0.41&2&1\\0&-1&0.18&0&0\\0.48&0&0&-1&0\end{pmatrix}\)
X=\(\begin{pmatrix}a\\b\\c\\d\\e\end{pmatrix}\)
B=\(\begin{pmatrix}10\\20\\0\\0\\0\end{pmatrix}\)
であり、Aの逆行列A-1を 求めることができればa,b,c,d,eを算出することができます。
逆行列を手計算でやるなら掃き出し法等で求めるのが一般的だと思いますが、5×5行列にもなってくるとかなり面倒ですよね。
そのため楽をするためにExcelやPythonを使用して計算します。
Excelでの計算法
ExcelではMINVERSE関数とMMULT関数を使用すれば楽に解を求めることができます。
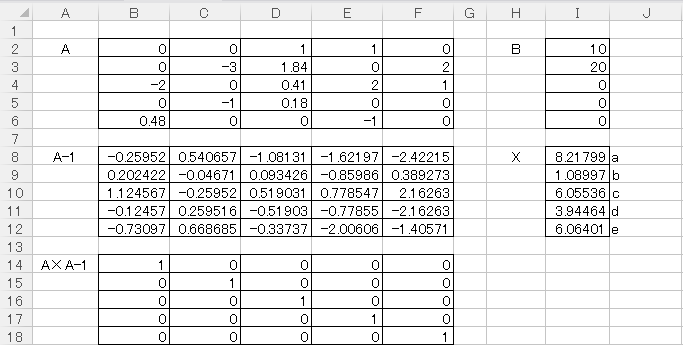
まずB2:F6にAの行列式を入力します。Bのベクトルも同様にI2:I6に入力します。
次に逆行列A-1をMINVERSE関数で求めます。
まず逆関数の計算結果を表示させるセルを複数選択し(ここではB8:F12)、
=MINVERSE(B2:F6)と入力します。括弧内はAの行列式を選択します。
そしてCtrl+Shift+Enterを入力すれば上図のように逆行列が計算されて結果が表示されます。
続いてXベクトルをMMULT関数で求めます。I8:I12を複数選択し、=MMULT(B8:B12,I2,I6)と入力してCtrl+Shift+Enterを押せば上図のように計算結果が表示されます。
正しく計算できていれば、
a=8.22
b=1.09
c=6.06
d=3.94
e=6.06
となり、(1)式の係数を求めることができました。
ちなみに検算方法の1つとして、A×A-1を計算して単位行列になるかどうかを確認しておくことが挙げられます。
B14:F18セルを複数選択し、=MMULT(B2:F6,B8,F12)と入力してCtrl+Shift+Enterを押せば A×A-1が計算されます。上図ではちゃんと単位行列になっていますね。
Pythonでの計算法
ライブラリ・モジュールのインポート
Pythonで行列式を扱う場合にはNumpyが非常に便利ですのでインポートします。
#numpyインポート
import numpy as np前提条件の入力
行列AとベクトルBをそれぞれ入力します。
#前提条件
A=np.array([[0,0,1,1,0],[0,-3,1.84,0,2],[-2,0,0.41,2,1],[0,-1,0.18,0,0],[0.48,0,0,-1,0]])
B=np.array([[10],[20],[0],[0],[0]])Aの逆行列算出
次にAの逆行列をlinalg.inv関数で算出します。
#Aの逆行列算出
Ainv=np.linalg.inv(A)たった1行の記述で逆関数を算出できます。便利ですね。
Xベクトル算出
続いてXベクトルを算出します。
Pythonではdot関数を使用することで行列の掛け算を行なうことができます。
#Xベクトル算出
X=np.dot(Ainv,B)結果の出力
最後に逆行列AinvとXベクトルの結果をprint関数で出力します。
#結果の出力
print(Ainv)
print(X)計算結果の確認
特に入力ミス等がなければ計算結果が以下のように表示されます。
[[-0.25951557 0.54065744 -1.08131488 -1.62197232 -2.42214533]
[ 0.20242215 -0.0467128 0.09342561 -0.85986159 0.38927336]
[ 1.12456747 -0.25951557 0.51903114 0.77854671 2.16262976]
[-0.12456747 0.25951557 -0.51903114 -0.77854671 -2.16262976]
[-0.73096886 0.66868512 -0.33737024 -2.00605536 -1.40570934]]
[[8.21799308]
[1.0899654 ]
[6.05536332]
[3.94463668]
[6.06401384]]計算結果が数字とグラフの両方で表示されます。
2~6行目までが逆行列Ainvの結果、7~11行目がXベクトルの結果です。
Excelでの計算結果と同じ値になっており、きちんと計算できていることが確認できました。
下に計算コードを最初から最後までまとめて載せておきます。
#numpyインポート
import numpy as np
#前提条件
A=np.array([[0,0,1,1,0],[0,-3,1.84,0,2],[-2,0,0.41,2,1],[0,-1,0.18,0,0],[0.48,0,0,-1,0]])
B=np.array([[10],[20],[0],[0],[0]])
#Aの逆行列算出
Ainv=np.linalg.inv(A)
#Xベクトル算出
X=np.dot(Ainv,B)
#結果の出力
print(Ainv)
print(X)まとめ
ExcelとPythonで連立一次方程式を逆行列で計算する方法を解説しました。
今回の例のように変数が多い場合には特に有用な手法です。
