概要
流体が壁面との摩擦や流体同士の摩擦によってエネルギーを損失することを圧力損失といいます。
流体にポンプ等でエネルギーをかけて移動させるとき、理論上はベルヌーイの定理が成り立ちます。
しかし実際は圧力損失が発生するため、その分のエネルギーを上乗せして流体に与える必要があります。
したがって、圧力損失を計算して見積もることは非常に重要です。
この記事では実務で計算する頻度の多い配管流路の圧力損失について計算方法を紹介します。
圧力損失の計算方法
直管
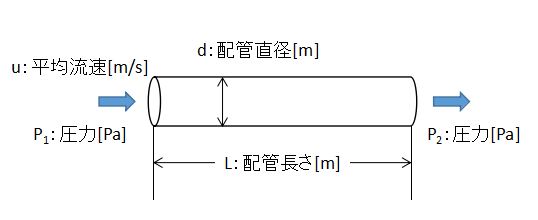
直管の圧力損失はファニングの式で計算することができます。
下の記事で詳しく解説しています。

(1)式がファニングの式です。
$$ΔP=4f\frac{ρu^{2}}{2}\frac{L}{d}・・・(1)$$
ΔP:圧力損失[Pa]、f:摩擦係数[-]、ρ:流体密度[kg/m3]
u:流体の平均速度[m/s]、L:配管長さ[m]、d:配管直径[m]
ポンプの揚程計算でヘッド[m]で計算するときは、(1)式の両辺をρgで割った(2)式を使用します。
$$h_{f}=4f\frac{u^{2}}{2g}\frac{L}{d}・・・(2)$$
hf:摩擦損失水頭[m]
配管流路の特殊形状
配管は直管だけで構成されているわけではなく、実際は曲がり部や拡大・縮小部、弁などの様々な形状をした流路が間にあります。
それらの特殊形状部による損失ヘッドを形状損失水頭hl[m]といいます。
$$h_{l}=f_{l}\frac{u_{m}^{2}}{2g}・・・(3)$$
形状損失水頭hlは基本的に(3)式のような形で表されます。
形状によって摩擦係数flの値が変化するため、実質は各形状の摩擦係数flを求めていくことになります。
急拡大による損失水頭
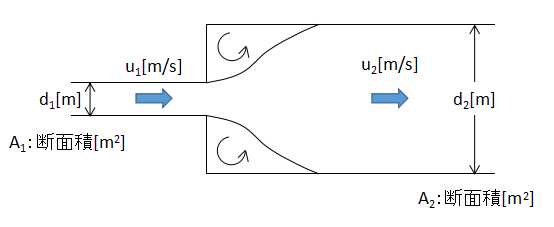
流路が急拡大する場合は、流れは流路形状にすぐ追従できないため急拡大部に渦が形成されます。
この渦はその場に留まる流れであり、流体を所定の場所まで送り届ける目的から言うと、明らかに無駄なエネルギーであり損失となっています。
急拡損失水頭hse[m]は、
$$h_{se}=f_{se}\frac{u_{1}^{2}}{2g}・・・(4)$$
$$f_{se}=(1-\frac{A_{1}}{A_{2}})^{2}=[(1-(\frac{d_{1}}{d_{2}})^{2})]^{2}・・・(5)$$
fse:急拡損失係数[-]、um:管内平均流速[m/s]、g:重力加速度[m/s2]
(4)、(5)式で表されます。
急縮小による損失水頭
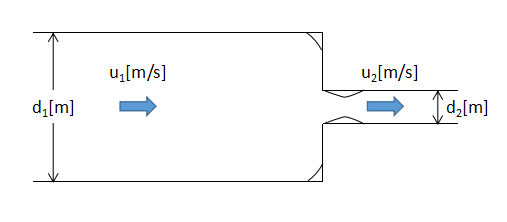
流路が急縮小する場合も同様に急縮小部で渦が発生し、エネルギーが損失します。
急縮小部による損失水頭hsc[m]は、
$$h_{sc}=f_{sc}\frac{u_{2}^{2}}{2g}・・・(6)$$
$$f_{sc}=(\frac{1}{C_{c}}-1)^{2}・・・(7)$$
fsc:急縮損失係数[-]、Cc:縮流係数[-]
(6)、(7)式で表されます。
縮流係数Ccは理論的には求めることができず、実験値を参照する必要があります。
参考書では縮流係数Ccそのものが与えられるか、もしくは急縮損失係数fscが直接与えられることもあります。
下表に配管の縮小比d2/d1に対する急縮損失係数fscを示します。
| d2/d1 | 急縮損失係数fsc |
| 0 | 0.50 |
| 0.1 | 0.50 |
| 0.2 | 0.49 |
| 0.3 | 0.49 |
| 0.4 | 0.46 |
| 0.5 | 0.43 |
| 0.6 | 0.38 |
| 0.7 | 0.29 |
| 0.8 | 0.18 |
| 0.9 | 0.07 |
| 1.0 | 0 |
入口損失水頭
大きなタンクから狭い配管内へ流体が流入するときに入口損失水頭が発生します。
入口損失水頭he[m]は、
$$h_{e}=f_{e}\frac{u_{m}^{2}}{2g}・・・(8)$$
fe:入口損失係数[-]
(8)式となります。
入口損失水頭feは入口形状によって異なります。
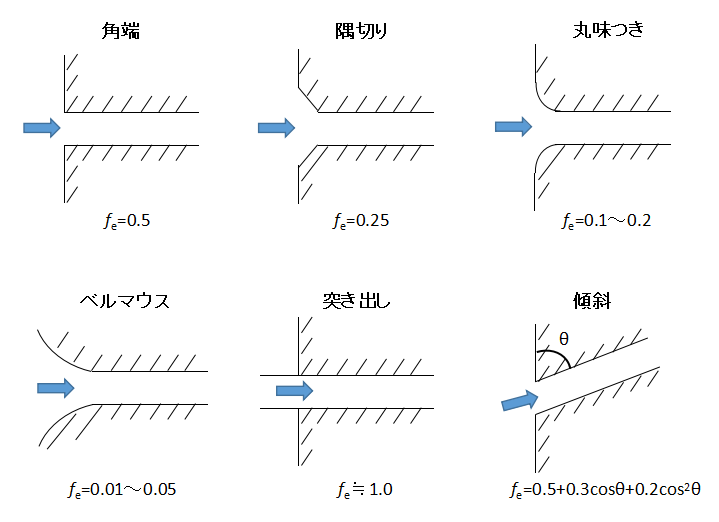
上図に代表的な入口形状と入口損失水頭feの値を示します。
出口損失水頭
狭い配管内から大きなタンク等へ流体が流出するときに出口損失水頭が発生します。
出口損失水頭ho[m]は、
$$h_{o}=f_{o}\frac{u_{1}^{2}}{2g}・・・(9)$$
fo:出口損失係数[-]
(9)式となります。
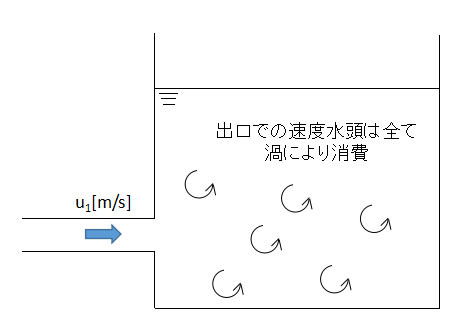
例えばタンク内に放流される場合において、流路出口での速度水頭は全てタンク内で渦を形成して消費されます。
したがって出口損失係数foは1を使用し、流路出口では速度水頭分が消費されるとすることが多いです。
漸拡大による損失水頭
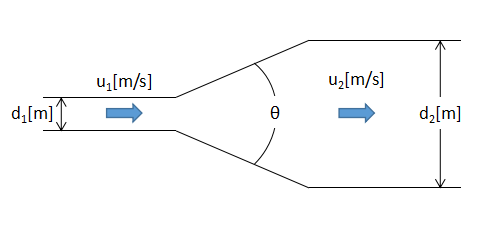
漸拡大する流路では急拡大する流路ほどではないですが、流れの剥離による渦が生じエネルギーが損失します。
漸拡損失水頭hge[m]は、
$$h_{ge}=f_{ge}f_{se}\frac{u_{1}^{2}}{2g}・・・(10)$$
fge:漸拡損失係数[-]、fse:急拡損失係数[-]
(10)式となります。
漸拡損失係数fgeは角度θによって変化するため、下の図から値を読み取り使用します。
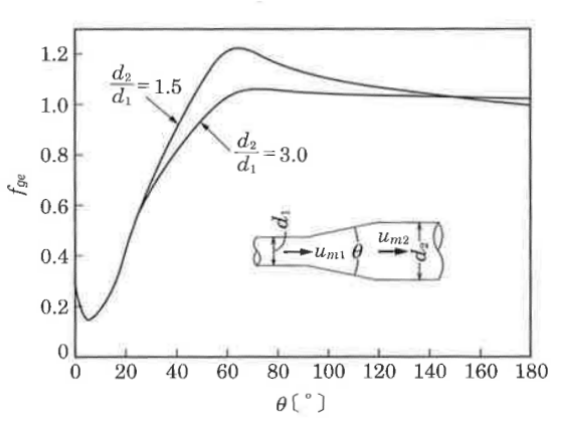
漸縮小による損失水頭
漸縮小する流路ではほとんどエネルギー損失がないため、圧力損失の計算では無視してよいでしょう。
曲管・弁による損失水頭
曲管・弁の圧力損失は、直管相当長さLe[m]を算出してファニングの式で求めるのが最も簡単な方法です。
過去に様々な実験がされており、各形状での圧力損失を直管で換算するとどのくらいの値になるかが各参考書に記載されています。
$$L_{e}=n・d・・・(11)$$
n:係数[-]、d:管直径[m]
直管相当長さLe[m]は(11)式で計算できます。
係数nについて代表的なものを下表に示します。
| 管挿入物 | n |
| 45°エルボ | 15 |
| 90°エルボ(標準曲率) | 32 |
| 90°ベンド(曲率/直径=3) | 24 |
| 90°ベンド(曲率/直径=4) | 10 |
| 180°ベンド | 75 |
| 十字継手 | 50 |
| T字継手 | 40~80 |
| 仕切り弁(全開) | 0.7 |
| 仕切り弁(1/4閉) | 10~40 |
| 仕切り弁(1/2閉) | 100~200 |
| 仕切り弁(3/4閉) | 800 |
| 玉形弁(全開) | 300 |
| アングル弁(全開) | 170 |
| 水量計(ピストン型) | 600 |
| 水量計(ディスク型) | 135~400 |
| 水量計(翼車型) | 200~300 |
| ユニオン | 0 |
| カップリング | 0 |
