概要
速度境界層と温度境界層の厚みの比を表わす無次元数をプラントル数Prといいます。
$$Pr=\frac{C_{p}μ}{k}・・・(1)$$
Pr:プラントル数[-]、Cp:流体比熱[J/(mol・K)]
μ:流体粘度[Pa・s]、k:流体の熱伝導度[W/(m・K)]
プラントル数は(1)式で表されます。
プラントル数を表わすパラメータは全て物質に固有な物性値となっており、レイノルズ数やヌセルト数と違って流れに依存しないのが特徴です。
また、プラントル数は熱交換器や撹拌槽の伝熱計算を行なううえで必要なパラメータです。
-

熱交換器【管内側境膜伝熱係数】を解説:チューブ内流れの伝熱
この記事では配管や熱交換器の伝熱管内を流れる流体の境膜伝熱係数についてまとめています。配管内の流動は他の流れに比べると単純で、種々の相関式が発表されています。
続きを見る
例えば上の記事に示すように、境膜伝熱係数を算出するための関係式にプラントル数が含まれています。
強制対流層の伝熱とプラントル数
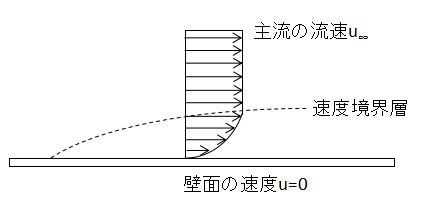
上図に示すような平板上の強制対流伝熱を考えます。
平板から十分離れた位置での流れは流速u∞で一定ですが、平板に近づくにつれ流体の持つ粘性抵抗によって流速が減少し、平板壁面では流速ゼロになります。
このように流速がゼロから主流の流速まで発達する領域のことを速度境界層といいます。
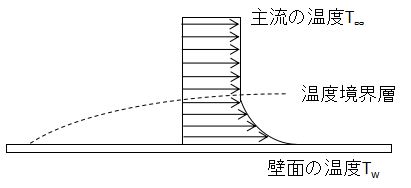
また、同様な平板上の流れで、今度は温度分布を上図に示します。
主流の温度T∞よりも平板の壁面温度Twの方が高いと、上図のように壁面に近いところでは温度が高く、主流に近づくにつれ冷えていくような温度分布になります。
このように壁面から主流の温度まで変化する領域のことを温度境界層といいます。
プラントル数はこれら速度境界層と温度境界層の厚みの比を意味しており、今回の例のような平板上の強制対流の層流熱伝達では、
$$\frac{δ}{δ_{T}}≒Pr^{1/3}$$
δ:速度境界層の厚み[m]、δT:温度境界層の厚み[m]
近似的に上式となることが知られています。
したがって、Pr≒1のときδ=δTとなり速度境界層と温度境界層の厚みが一致します。
Pr>1のときは速度境界層の厚みδの方が大きくなり、Pr<1のときは温度境界層の厚みδTの方が大きくなります。
一般にPr>1のときは粘度の高い流体であることが多く、Pr<1のときは粘度の低い流体であることが多いです。(主要な流体のプラントル数については後述します。)
また、装置設計という観点から言うと、Prの大小と伝熱性能は非常に複雑な関係にあります。
$$Nu=\frac{hD}{k}=a・Re^{α}Pr^{β}$$
一般に熱交換器や撹拌槽の伝熱計算に使用される関係式を上に示します。
レイノルズ数の指数であるαは0.6~0.8程度の値、プラントル数の指数であるβは0.33前後であることが多いです。
したがって、装置の伝熱性能を表わす境膜伝熱係数hはプラントル数が大きいほど高い値を示すため、伝熱性能が良いことになります。
ただしこれはあくまでプラントル数のみに注目した場合であるため、実際の伝熱性能はレイノルズ数についても考慮する必要があります。
主要な流体のプラントル数
各物質の大まかなプラントル数を以下に示します。
| 物質 | プラントル数 |
| 液体金属(Sn、Pb、Zn、Sb、Al、Fe) | Pr≒0.01~0.03 |
| 気体(Air、He、H2、O2、N2) | Pr≒0.7 |
| 水 | Pr≒6~7 |
| 潤滑油 | Pr>>1 |
特に気体のPr≒0.7、水のPr≒0.6~0.7は覚えておくと便利です。
プラントル数に含まれるパラメータは単位系が一致していないことが多く(calやJ)、合うように単位変換する必要があります。
単位変換の際に意外と間違えやすいため、プラントル数のおおよその値を覚えておけば検算できます。
まとめ
プラントル数について解説しました。
熱交換器等の伝熱機器の設計には欠かせない無次元数です。
