【充填塔】圧力損失の計算方法を紹介

概要

一般的な圧力損失ΔPと断面積当たりのガス流速の関係を下の図に示します。

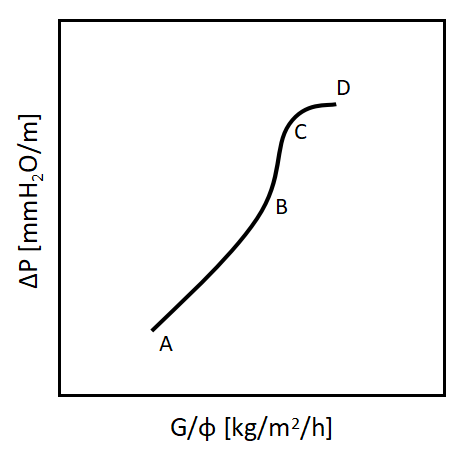
A～Bの区間は液ガス流量が少なく、圧力損失ΔPはガス流速Gの1.8～2.0乗に比例して増大します。

B点に達すると、ガスが液の一部を持ち上げるようになり圧力損失がその分増大します。
図からもわかるように、ガス流速Gの2.0乗より大きい値に比例するようになり、傾きが増大しています。B点をローディング点といいます。

C点付近になると、ガスがほとんどの液を持ち上げるようになります。
C点をフラッディング点といい、液が塔底から缶出せず、塔頂から溢れ出るため、充填塔としての操作ができない領域になります。

C点を超え、C～Dの区間になると、塔内の連続相が逆転し、いわゆる気泡塔の操作範囲に入ってきます。
気泡塔では、液のホールドアップを保つためにガス流量を多めに流しているわけですね。

充填塔の圧力損失は、他の機器に比べると比較的小さいですが、送風機の所要動力を決定するうえで重要になります。

本記事では充填塔の圧力損失の計算方法について紹介します。

圧力損失の計算方法

Levaの式

向流式の充填塔で、ローディング速度以下の運転条件であれば、Levaの実験式を使用して圧力損失を計算できます。

$$\frac{ΔP}{Z}=α(10^{βL/ρ_{L}})(\frac{G^{2}}{ρ_{G}})$$

ΔP：圧力損失[Pa]、Z：充填高さ[m]、L：液の質量速度[kg/m²/s]
G：ガスの質量速度[kg/m²/s]、ρ_G：ガス密度[kg/m³]、ρ_L：液密度[kg/m³]
α,β：定数

ラシヒリング、ベルルサドル、インタロックスサドルのような汎用的な充填物に関して適用できます。

充填物メーカーのデータを利用する

汎用的な充填物に関してはLevaの式で圧力損失を計算できますが、メーカー特有の充填物となると係数の値がわからないので計算できません。

そんな場合には、メーカーのサイトや発行論文を調べてみましょう。
圧力損失のデータや実験式が公表されている場合があります。

また、充填物の大手メーカーは、自社充填物の圧力損失やキャパシティを計算するためのソフトを無料で公開していることもあります。

有名なところでは、

Koch-Glitsch(コーク-グリッヂ)社のKG-TOWER

www.koch-glitsch.com

 

1 Pocket

KG-TOWER® Software | Koch-Glitsch

https://www.koch-glitsch.com/kg-tower-software

Koch-Glitsch is a subsidiary of Koch Industries and is recognized as a global solutions provider of mass transfer and separations equipment and technologies.

Sulzer(スルザー)社のSulcol

www.sulzer.com

Sulcol™ for Windows

https://www.sulzer.com/en/shared/products/sulcol-for-windows

Use this Sulzer tool to design your mass transfer columns.

があります。
ユーザー情報を入力すれば無料でダウンロードして使用することができます。

但し、ソフト中でどのような式や係数で計算しているかは開示されていないことがあります。
もし計算結果が明らかにおかしいと思う場合は、問い合わせてみるのも手です。