【Python】黄金分割法の解説：最急降下法の学習率最適化

概要

黄金分割法は最適化手法の1つであり、非線形最小二乗法や最適化問題に使用します。

この手法は関数の微分値を必要としないため簡単に計算できる一方で、複数の極値を持つような複雑な関数の最適化には向いていません。

この記事では最急降下法で使用する学習率αを、固定値ではなくステップごとに値を最適化するために黄金分割法を使用してみます。

原理

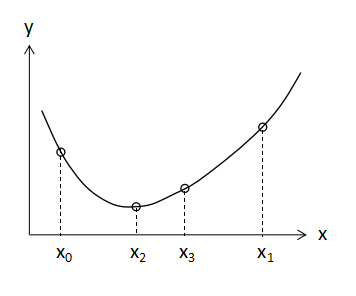
黄金分割法を適用する前提条件として、上図に示すように分割する区間で下に凸の関数である必要があります。

ここではある関数f(x)の区間[x₀,x₁]の間にある最小値を求めることを考えます。

区間内で新たにx₁,x₂という点を作成して区間を分割します。x1,x2はそれぞれ、

$$x_{2}=x_{0}+γ(x_{1}-x_{0})・・・(1)$$

$$x_{3}=x_{1}-γ(x_{1}-x_{0})・・・(2)$$

(1),(2)式で表されます。

このときの分割比γは、

$$γ=\frac{-1+\sqrt{5}}{2}≒0.618・・・(3)$$

(3)式となります。この0.618という数字はいわゆる黄金比と呼ばれるもので、この比率で区間分割を繰り返す手法であるため黄金分割法と呼ばれています。

分割後のx₂とx₃の値の平均値を取って所定の許容誤差toleranceと比較し、

$$\frac{\left|x_{2}-x_{3}\right|}{2}<tolerance・・・(4)$$

となれば収束して最小値が算出できたと判定します。

(4)式が成り立たなければf(x₂)とf(x₃)の値を比較して、

$$f(x_{2})>f(x_{3})・・・(5)$$

(5)式であれば区間x₂～x₁の間に最小値があることがわかるので、次のステップではx₀をx₂に更新して(1),(2)式の計算を繰り返します。逆に

$$f(x_{2})<f(x_{3})・・・(6)$$

(6)式であれば区間x₀～x₃の間に最小値があることがわかるので、次のステップではx₁をx₃に更新して(1),(2)式の計算を繰り返します。

このように少しずつ区間の値を狭めていくことで最終的には(4)式を満たす最小値にたどり着きます。

Pythonでの計算法

以前の記事で最急降下法について紹介しました。

: 【Python】最急降下法の解説：回分操作コストの最小化計算
本記事では非線形最小二乗法の計算手法の1つである最急降下法について解説します。他の手法と比較して簡単に計算できますが、繰り返し計算回数が多くなり収束しにくいのが欠点です。
続きを見る

今回は同じ計算例で学習率αを黄金分割法で最適化してみましょう。

計算条件

詳しい計算条件は以前の記事で紹介していますので今回は割愛します。

目的関数は(7)式です。

$$C_{T}=C_{p}×N_{c}+C_{AF}=(30x^{0.25}+21)\frac{1000000}{x}+340x^{0.8}+260000・・・(7)$$

(7)式の総コストC_Tが最小になるよう最急降下法と黄金分割法を使用して計算しましょう。

ライブラリ・モジュールのインポート

ここからPythonでの記述となります。

Numpyをインポートします。

#モジュールインポート
import numpy as np

前提条件

問題で与えられた前提条件を入力します。

#前提条件
cop=20  #運転期間のコスト[$/h]
cpp=15  #準備期間のコスト[$/h]
P=1000000  #年間生産量[kg/y]
raw=260000  #原材料費とその他諸経費[$/y]

目的関数

(7)式の目的関数をdef文で定義します。

目的関数
def f(x):
    opcost=cop*1.5*x**0.25+cpp*1.4 
    return opcost*P/x+340*x**0.8+raw

黄金分割法の入力

元の記事を大いに参考にさせていただきました。

入力内容は前述した計算を行なっています。

関数として黄金分割法の計算を入力し、後述する最急降下法の記述で呼び出します。

#黄金分割法による学習率最適化
def goldenRatioSearch(function, range, tolerance):
    gamma = (-1+np.sqrt(5))/2
    a = range[0]
    b = range[1]
    p = b-gamma*(b-a)
    q = a+gamma*(b-a)
    Fp = function(p)
    Fq = function(q)
    width = 1e8
    while width > tolerance:
        if Fp <= Fq:
            b = q
            q = p
            Fq = Fp
            p = b-gamma*(b-a)
            Fp = function(p)
        else:
            a = p
            p = q
            Fp = Fq
            q = a+gamma*(b-a)
            Fq = function(q)
        width = abs(b-a)/2
    alpha = (a+b)/2
    return alpha

偏微分と勾配の計算

最急降下法に必要な微分の計算を行なっています。

#偏微分と勾配の計算
def numerical_diff(f, x, i):
    h=1e-4
    h_vec=np.zeros_like(x)
    h_vec[i]=h
    return (f(x+h_vec)-f(x-h_vec))/(2*h)  #数値微分

def numerical_gradient(f, x):
    grad=np.zeros_like(x)
    for i, _ in enumerate(x):
        grad[i]=numerical_diff(f, x, i)
    return grad

最急降下法の入力

メインの最急降下法を入力します。

#最急降下法
def gradient_descent(f,initial_position,alpha,flag):
    x=initial_position
    n=1  #計算回数初期値
    error=10  #エラーの初期値
    ex=1E-4  #収束判定値
    while error > ex:
        grad=numerical_gradient(f, x)
        if flag == 1:
            alpha = goldenRatioSearch(lambda alpha:f(x-alpha*grad), [0, 1], 1e-4)
        else:
            alpha = 1
        x_new=x-alpha * grad 
        error=abs(x_new-x)
        print(n,x_new,alpha,error)
        x=x_new
        n=n+1

    return x_new

今回はwhile文で収束判定値以下になれば計算を終了するように記述しました。

初期値入力

計算に必要な初期値を入力しています。

学習率αの初期値はとりあえず0.1としました。

#初期条件
alpha=0.1
flag=1
initial_position=[1000.]

最急降下法の実行と出力

定義した最急降下法の実行と出力を記述しています。

#最急降下法の実行と出力
min_pos = gradient_descent(f,initial_position,alpha,flag)  #最急降下法の実行
CTmin=f(min_pos)
tmin=1.5*min_pos**0.25+1.4
print('総コストが最小となる1バッチ当たりの生産量[kg/cycle]: {0}'.format(min_pos))
print('総コスト最小値[$/y]: {0}'.format(CTmin))
print('総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: {0}'.format(tmin))

計算結果の確認

特に入力ミス等がなければ以下のように結果が表示されます。


1 [1079.19663279] 0.9999134648641439 [79.19663279]
2 [1140.66026998] 0.9999134648641439 [61.46363719]
3 [1190.74600659] 0.9999134648641439 [50.08573661]
4 [1232.79219206] 0.9999134648641439 [42.04618547]
5 [1268.80969999] 0.9999134648641439 [36.01750793]
6 [1300.11912375] 0.9999134648641439 [31.30942376]
7 [1327.64146428] 0.9999134648641439 [27.52234054]
8 [1352.04823204] 0.9999134648641439 [24.40676776]
9 [1373.84610443] 0.9999134648641439 [21.79787239]
10 [1393.42795818] 0.9999134648641439 [19.58185375]
11 [1411.10527657] 0.9999134648641439 [17.67731839]
12 [1427.1296195] 0.9999134648641439 [16.02434292]
13 [1441.70734056] 0.9999134648641439 [14.57772107]
14 [1455.00998212] 0.9999134648641439 [13.30264156]
15 [1467.18180082] 0.9999134648641439 [12.1718187]
show more (open the raw output data in a text editor) ...

197 [1625.83841021] 0.9899704306932211 [0.00010488]
198 [1625.83850815] 0.9839322609346497 [9.79357962e-05]
総コストが最小となる1バッチ当たりの生産量[kg/cycle]: [1625.83850815]
総コスト最小値[$/y]: [516076.92323895]
総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: [10.92490407]

198回目の計算で計算が収束しました。学習率はほぼ1に近い値で計算されています。計算結果の値はこちらの記事の値とほぼ同じになっています。

ちなみに、学習率を0.1で固定して同じ計算をした場合は、1652回目の計算で収束しました。黄金分割法で学習率を最適化した方が計算回数を少なくできることがわかりました。

全体のコードを下に載せておきます。

#モジュールインポート
import numpy as np

#前提条件
cop=20  #運転期間のコスト[$/h]
cpp=15  #準備期間のコスト[$/h]
P=1000000  #年間生産量[kg/y]
raw=260000  #原材料費とその他諸経費[$/y]

#目的関数
def f(x):
    opcost=cop*1.5*x**0.25+cpp*1.4 
    return opcost*P/x+340*x**0.8+raw

#黄金分割法による学習率最適化
def goldenRatioSearch(function, range, tolerance):
    gamma = (-1+np.sqrt(5))/2
    a = range[0]
    b = range[1]
    p = b-gamma*(b-a)
    q = a+gamma*(b-a)
    Fp = function(p)
    Fq = function(q)
    width = 1e8
    while width > tolerance:
        if Fp <= Fq:
            b = q
            q = p
            Fq = Fp
            p = b-gamma*(b-a)
            Fp = function(p)
        else:
            a = p
            p = q
            Fp = Fq
            q = a+gamma*(b-a)
            Fq = function(q)
        width = abs(b-a)/2
    alpha = (a+b)/2
    return alpha

#偏微分と勾配の計算
def numerical_diff(f, x, i):
    h=1e-4
    h_vec=np.zeros_like(x)
    h_vec[i]=h
    return (f(x+h_vec)-f(x-h_vec))/(2*h)  #数値微分

def numerical_gradient(f, x):
    grad=np.zeros_like(x)
    for i, _ in enumerate(x):
        grad[i]=numerical_diff(f, x, i)
    return grad

#最急降下法
def gradient_descent(f,initial_position,alpha,flag):
    x=initial_position
    n=1  #計算回数初期値
    error=10  #エラーの初期値
    ex=1E-4  #収束判定値
    while error > ex:
        grad=numerical_gradient(f, x)
        if flag == 1:
            alpha = goldenRatioSearch(lambda alpha:f(x-alpha*grad), [0, 1], 1e-4)
        else:
            alpha = 1
        x_new=x-alpha * grad 
        error=abs(x_new-x)
        print(n,x_new,alpha,error)
        x=x_new
        n=n+1

    return x_new

#初期条件
alpha=0.1
flag=1
initial_position=[1000.]

#最急降下法の実行と出力
min_pos = gradient_descent(f,initial_position,alpha,flag)  #最急降下法の実行
CTmin=f(min_pos)
tmin=1.5*min_pos**0.25+1.4
print('総コストが最小となる1バッチ当たりの生産量[kg/cycle]: {0}'.format(min_pos))
print('総コスト最小値[$/y]: {0}'.format(CTmin))
print('総コストが最小となる場合の1サイクルにかかる時間[h/cycle]: {0}'.format(tmin))

まとめ

最急降下法の学習率αを最適化するために黄金分割法を使用した計算をしてみました。

あらかじめ分割区間がわかっているパラメータであれば黄金分割法を使用しやすいと思います。