【ビオ数】について解説：固体表面の熱伝達と固体内部の熱伝導の比

概要

固体表面の熱伝達と固体内部の熱伝導の比を表わす無次元数をビオ数Biといいます。

$$Bi=\frac{hL}{k_{s}}・・・(1)$$

Bi：ビオ数[-]、h：固体表面の熱伝達率[W/(m²K)]

L：代表長さ=固体の体積V/固体の表面積S[m]、k_s：固体の熱伝導度[W/(mK)]

ビオ数は(1)式で表されます。

式の形はヌセルト数Nuと全く同じですが、ヌセルト数は流体の熱伝導度を使用するのに対して、ビオ数は固体の熱伝導度を使用します。

ビオ数が小さいと固体表面の熱伝達より固体内部の熱伝導が支配的となり、固体表面から固体内部まで一瞬で熱が伝わります。

一方でビオ数が大きいと固体内部の熱伝導が遅いため、固体表面から固体内部まで熱が伝わるのに時間がかかり温度分布が生じます。

実用上は、固体内部の熱伝導をどれだけ簡略化して計算するかの指標となります。

ビオ数は固体の温度が時間経過で変化する場合に考慮するのが一般的です。

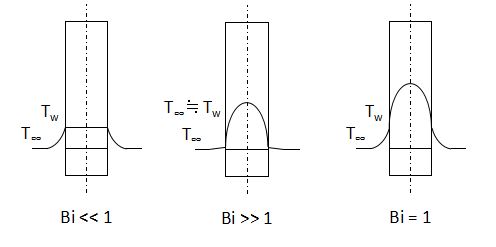
上図に例として、ある時間tにおけるビオ数の違いによる固体平板内の温度分布を示します。

前提として固体周りの流体温度が低く、固体が経時変化でどんどん冷えていくような過渡熱伝導を考えます。

固体の熱伝導度kが十分に大きい、あるいは固体が十分に小さいような場合はBi<<1となります。

このとき固体の熱伝導は瞬時に起こり、固体内部の温度はほぼ一様とみなせます。

したがって、固体の伝熱は固体表面の熱伝達率と固体の熱容量で決まります。

このような物体内の温度分布を無視して熱容量だけを集中系として取り扱うことのできるモデルを集中熱容量モデルといいます。

(集中系というのは、位置依存性がなく時間に関する常微分方程式で表せるという意味合いです。固体内に温度分布がある場合は位置依存性があるので、位置と時間に関する偏微分方程式を解く必要があります。)

仮に、ある高温の固体が周囲の流体で冷やされる系について考えます。

微小時間dtの間に温度がdTだけ変化するときの熱収支を集中熱容量モデルで表すと、(2)式となります。

$$c_{p}ρV\frac{dT}{dt}=-hS(T-T_{∞})・・・(2)$$

c_p：固体の比熱[J/(kg・K)]、ρ：固体の密度[kg/m³]、V：固体の体積[m³]

h：固体表面の熱伝達率[W/(m²K)]、S：固体の表面積[m²]

(2)式をt=0のときT=T₀として積分すると、

$$\int_{T_{0}}^{T}\frac{dT}{T-T_{∞}}=-\frac{hS}{c_{p}ρV}\int_{0}^{t}dt$$

$$\frac{T-T_{∞}}{T_{0}-T_{∞}}={\rm{exp}}(-\frac{hS}{c_{p}ρV}t)・・・(3)$$

(3)式となり、経時変化したときの固体内部の温度Tを簡単に求めることができます。

また、一般にBi<0.1であれば集中熱容量モデルで計算しても誤差は数%以下なので、簡易的な計算には十分適用できるでしょう。

固体の熱伝導度kが小さい、あるいは固体が十分に大きいような場合はBi>>1となります。

このとき固体の熱伝導は遅く、固体内部には温度分布が生じます。

一方で、固体表面の熱伝達は固体内部の熱伝導より十分に速く、表面温度T_wが瞬時に外部のバルク温度T_∞と等しくなります。

そのためT_∞=T_wとして固体表面の境界条件を設定して計算することができ、固体内の温度分布は熱伝達率に依存しなくなります。

固体表面の熱伝達と固体内部の熱伝導の移動熱量が同程度であるとき、Bi=1となります。

この場合は熱伝達と熱伝導どちらの影響もありますから、計算モデルを簡略化することができません。

固体表面の熱伝達と固体内部の熱伝導のどちらも表現できるように、計算モデルを組む必要があります。

モデルの形状が複雑な場合や境界条件が複雑な場合は、自分で式を立てて解くのは難しいです。

このときは3Dモデルを作成し熱流体シミュレーションソフトで計算するのが1つの手です。

ビオ数について解説しました。

固体内部の伝熱計算をするときはビオ数を計算してみましょう。