概要
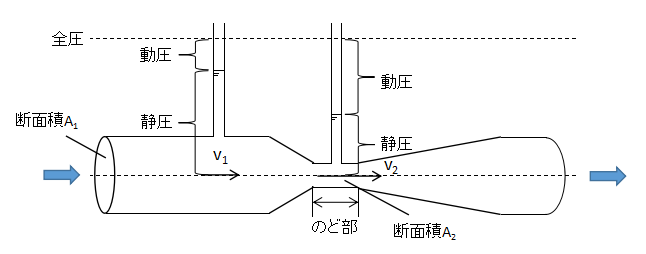
上図のようにゆるやかな縮小部と拡大部を持つ管をベンチュリー管と呼びます。
ベンチュリー管は動圧と静圧の異なる箇所を作り出し、各々の箇所の静圧差を測定することで流速及び流量を測定できます。
上図の液柱は、仮に摩擦損失が無視でき、全圧一定とみなせる場合の動圧と静圧のバランスを示しています。
動圧と静圧とは、ベルヌーイの式で言うところの速度水頭、圧力水頭を示しています。
ベンチュリー管で管路縮小前を添え字1、管路縮小後を添え字2としてベルヌーイの式を立てると、
$$\frac{1}{2}ρ{v_{1}}^{2}+ρgz_{1}+p_{1}=\frac{1}{2}ρ{v_{2}}^{2}+ρgz_{2}+p_{2}・・・(1)$$
(1)式となります。
通常、ベンチュリー管は水平に設置しますから、z1=z2となるため、
$$\frac{1}{2}ρ{v_{1}}^{2}+p_{1}=\frac{1}{2}ρ{v_{2}}^{2}+p_{2}・・・(2)$$
(2)式に簡略化されます。
(2)式において、左辺及び右辺第一項が動圧、第二項が静圧を示しています。
管路縮小前は流速が遅いため、動圧が小さく、静圧が大きい状態です。
非圧縮性流体であれば体積流量が一定であるため、管路断面積の変化前・変化後で、
$$Q=v_{1}A_{1}=v_{2}A_{2}・・・(3)$$
(3)式が成り立ちます。
したがって、管路縮小後の速度v2は、
$$v_{2}=v_{1}\frac{A_{1}}{A_{2}}・・・(4)$$
(4)式となります。
A1>A2なので、管路縮小後の速度v2は、管路縮小前の速度v1より必ず速くなります。
したがって、(2)式の右辺では動圧が大きく静圧が小さくなるよう変化します。
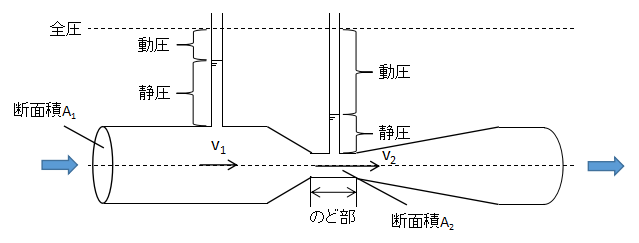
上図の液柱は静圧の大きさを表わしており、管路縮小前の方が静圧が大きいため液柱の高さが高く、縮小後は静圧が小さいため、高さが低くなります。
このように、管路断面積の変更により動圧と静圧が異なる状態が作れることを流量測定にうまく利用しています。
マノメータによる流量測定
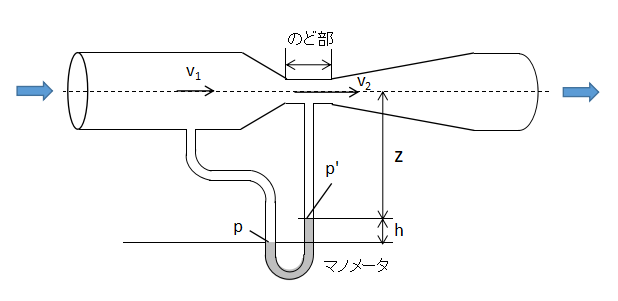
通常は管路縮小前の箇所と縮小後ののど部にマノメータ(差圧計)が付いており、静圧差を測定します。
資格試験等には上図のようなU字型のマノメータが出やすいと思います。
マノメータには配管内を流れる流体とは混ざらず、密度が重い液体(水銀等)を封入します。
前述したように、のど部の静圧が小さく、管路縮小前の静圧が大きいので、封入液は上図のような高さ関係になるはずです。
したがって、管路縮小前後の静圧差はマノメータ封入液の高さの差hと等しくなります。
この関係について、配管中心を基準高さとしてベルヌーイの式を立てると、
$$ρg(z+h)+p_{1}=ρgz+ρ_{c}gh+p_{2}$$
$$p_{1}-p_{2}=(ρ_{c}-ρ)gh・・・(5)$$
静圧差p1-p2は(5)式で算出することができます。
また、ベルヌーイの式である(2)式に(3)式を代入し、v1を消去します。
$$\frac{1}{2}ρ{v_{2}\frac{A_{2}}{A_{1}}}^{2}+p_{1}=\frac{1}{2}ρ{v_{2}}^{2}+p_{2}$$
$$v_{2}=\sqrt{\frac{\frac{2}{ρ}(p_{1}-p_{2})}{1-(\frac{A_{2}}{A_{1}})^{2}}}・・・(6)$$
(6)式となります。
(6)式に(5)式を代入し、静圧差p1-p2を消去すると、
$$v_{2}=\sqrt{\frac{\frac{2gh}{ρ}(ρ_{c}-ρ)}{1-(\frac{A_{2}}{A_{1}})^{2}}}・・・(7)$$
(7)式となり、既知のパラメータからのど部の流速v2を算出することができます。
流量Qを算出する場合は、のど部の断面積A2をかけます。
$$Q=A_{2}\sqrt{\frac{\frac{2gh}{ρ}(ρ_{c}-ρ)}{1-(\frac{A_{2}}{A_{1}})^{2}}}・・・(8)$$
ただし、実際にはベンチュリー管で摩擦損失が発生するため、流量係数Cで補正することもあります。
$$Q=CA_{2}\sqrt{\frac{\frac{2gh}{ρ}(ρ_{c}-ρ)}{1-(\frac{A_{2}}{A_{1}})^{2}}}・・・(9)$$
おわりに
ベンチュリー管について解説しました。
流量計の測定原理について理解しておくことは実務上重要ですし、このような内容は資格試験にも出題されやすいです。
