概要
一般に温度が高くなると反応速度は速くなります。このような温度依存性を表わす式をアレニウスの式といい、
$$k=A{\rm{exp}}(-\frac{E}{RT})・・・(1)$$
k:反応速度定数、A:頻度因子、E:活性化エネルギー
R:気体定数、T:温度
(1)式で表されます。
大学では化学系、化学工学系の学科であれば必ず習うと思いますし、化学系の会社でも当たり前のように使う式なので非常に重要です。
本記事ではアレニウスの式を線形プロットして頻度因子Aと活性化エネルギーEを算出するアレニウスプロットについて解説します。
アレニウスプロット
(1)式の両辺対数を取ると、
$${\rm{ln}}k={\rm{ln}}A-\frac{E}{R}\frac{1}{T}・・・(2)$$
(2)式となります。
(2)式を縦軸lnk、横軸1/Tでプロットすることで、傾き-E/R、切片lnAの直線が得られます。
この傾きと切片の値から、頻度因子A、活性化エネルギーEをそれぞれ求めることができます。
計算例1
まずはテストに出そうな計算例をやってみます。
| 温度T[℃] | 反応速度定数k[min] |
| 20 | 2010 |
| 30 | 11600 |
| 40 | 47500 |
| 45 | 102000 |
上の表に示す温度と反応速度定数でアレニウスプロットをしてみましょう。
まずは温度の増加とともに反応速度定数がきちんと増加していることを確認してください。今回は問題なさそうですね。
次に1/Tとlnkの値を算出します。
| 温度T[℃] | 1/T[1/K] | 反応速度定数k[min] | lnk |
| 20 | 0.00341 | 2010 | 7.606 |
| 30 | 0.00330 | 11600 | 9.359 |
| 40 | 0.00319 | 47500 | 10.768 |
| 45 | 0.00314 | 102000 | 11.533 |
注意点として、1/Tにするときは単位を℃からKに変換することです。例えば20℃では1/(20+273.15)≒0.00341となります。
1/Tは上表のようにだいたい10-3くらいのt小さい値となるのが普通です。
次に求めた値をグラフにプロットしてみましょう。
表計算ソフトであればプロットに対して近似直線を簡単に引くことができます。
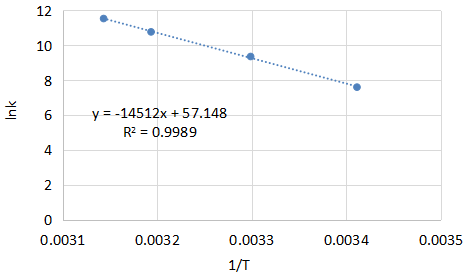
ソフトだと今回きれいに直線を引くことができましたが、テストだと方眼紙に定規で直線を引くことになるかもしれません。
テストに出るようなアレニウスプロットはきれいに直線を引ける問題しか出ないと思いますので、きれいに引けなければ計算ミスやプロットミスを疑ってください。
次にアレニウスプロットから傾きと切片を得ます。表計算ソフトの場合は近似直線の式を表示させて値を読み取るのが簡単です。
何回もアレニウスプロットを引き直す予定がある場合は、SLOPE関数で傾き、INTERCEPT関数で切片を得ることができます。
まずは傾きから計算します。
$$-14512=-\frac{E}{R}$$
$$E≒120650J/mol=120.7kJ/mol$$
活性化エネルギーは120.7kJ/molとなります。活性化エネルギーは普通kJ/mol表示で表すことが多いです。
次に切片を計算します。
$${\rm{ln}}A=57.148$$
$$A=6.6×10^{24}$$
頻度因子は6.6×1024となります。反応によりますが、頻度因子はかなり大きな値となります。
ちなみに、頻度因子の単位は反応速度定数kと等しくなります。例えばこの反応が一次反応の場合は反応速度定数k[1/s]となるため、頻度因子A[1/s]となります。
計算例2
計算例1では反応速度定数kが与えられていました。
しかし実際に実験データを取得することを考えると、反応速度定数kを直接測定することはできません。そのため、実験で測定できるデータから反応速度定数kを算出するところからやる必要があります。
反応速度定数算出のためには、
- 回分式反応器
- 測定項目:サンプル取得時間、温度、サンプル濃度
以上のような実験をやることが多いです。サンプル取得タイミングは、なるべく濃度変化の大きい反応初期にたくさんサンプリングするのが望ましいです。
反応後期になると系の濃度変化がほとんどなくなるため、誤差が大きくなります。
反応次数が既知の場合
仮に求めたい系の反応次数が既知の場合、実験データから簡単に反応速度定数kを算出することができます。
ここでは仮に一次反応だとすると回分式反応器の設計方程式から、
$$-\frac{dC_{A}}{dt}=kC_{A}・・・(3)$$
(3)式が成り立ちます。
(3)式を時間t=0~t、濃度CA=CA0~CAまで積分すると、
$$k=-\frac{1}{t}{\rm{ln}}(\frac{C_{A}}{C_{A0}})・・・(4)$$
CA0:成分Aの初濃度、CA:成分Aの時間tにおける濃度
(4)式となります。もしくは、
$$C_{A}=C_{A0}(1-x_{A})・・・(5)$$
xA:転化率[-]
(5)式から転化率xAを使用すると、
$$k=-\frac{1}{t}{\rm{ln}}(1-x_{A})・・・(6)$$
(6)式となります。
したがって、(4)式もしくは(6)式を使用して反応速度定数kを算出することができます。
反応次数が未知の場合
反応次数が未知の場合、反応次数を決定するところからやらなければなりません。
実験データの取得方法は既知の場合と同じですが、反応次数決定のために線形プロットをする必要があるぶん、データをたくさん取得する方が精度が上がります。
微分法
回分式反応器の設計方程式から、反応次数がn次の場合、
$$-\frac{dC_{A}}{dt}=kC_{A}^{n}・・・(7)$$
(7)式となります。
(7)式の両辺対数を取ると、
$${\rm{ln}}(-\frac{dC_{A}}{dt})={\rm{ln}}k+n{\rm{ln}}C_{A}・・・(8)$$
(8)式となります。
したがって、縦軸ln(-dCA/dt)、横軸lnCAでプロットすれば、傾きn、切片lnkの直線が得られます。
あとはどのようにしてdCA/dtの値を得るか、ということですが反応次数の記事で詳しく解説しています。
積分法
反応次数を0次、1次、2次などと仮定して回分式反応器の設計方程式を解く手法です。
この手法も反応次数の記事で詳しく解説しています。
アレニウスプロットが直線にならない場合
アレニウスプロットが直線にならないことはよくあります。原因をいくつか挙げます。
測定データの誤差
測定データの誤差、もしくはうまくデータを測れていないことが考えられます。
例えば実験ではサンプル取得後に反応停止剤を入れて反応を止めるのが望ましいです。
しかし適切な反応停止剤がない場合は反応が止まらないので、サンプル取得時間とサンプル濃度を測定した時間にずれが生じます。
測定データ誤差の対策としては、
- サンプル取得後なるべく早く測定する
- サンプル取得後に冷却して反応速度を遅くする
- サンプルを希釈して反応速度を遅くする
- 数回測定して平均値を出す
などを実施することで、精度を向上できます。
物質移動律速となっている
異相系の反応で、反応速度が十分に速く物質移動が遅いと、反応速度が物質移動速度で頭打ちになってしまうことがあります。これを物質移動律速といいます。
この状態になると物質移動速度が反応速度として観測されてしまうので、正しく反応速度の評価ができません。
対策としては、
- 物質移動速度を速くする
- 反応器の撹拌速度を速くする
- 原料の投入位置を混ざりやすい場所に変える
- 反応速度を遅くする
- 温度を下げる
- 原料濃度を低くする
などを行なうことで、相対的に反応速度よりも物質移動速度を速くすることが挙げられます。
単一の反応でない
複数の反応が起こっている場合はうまくアレニウスプロットに乗らないことがあります。
あらかじめ起こっている反応が予測できる場合はやりようがありますが、そもそも何の副反応が起こっているかわからない場合はかなり難しいです。
対策としては、
- 主反応以外の反応を抑えるように実験条件を調整する
- 反応速度式が既知の場合、測定データから各反応で消費された原料濃度を算出して使用する
などが挙げられます。1つ目の対策ができればベストですが、そう都合の良い実験条件はないことが多いです。
2つ目の測定データから実質濃度を算出する方が現実的です。
おわりに
アレニウスの式、アレニウスプロットについて解説しました。
測定データから頻度因子と活性化エネルギーを算出できる手法です。大学でも会社でもよく使用される式ですのでよく覚えておきましょう。
