概要
配管の圧力損失計算で使用される式をファニングの式といい、(1)式で表されます。
$$ΔP=4f\frac{ρu^{2}}{2}\frac{L}{d}・・・(1)$$
ΔP:圧力損失[Pa]、f:摩擦係数[-]、ρ:流体密度[kg/m3]
u:流体の平均速度[m/s]、L:配管長さ[m]、d:配管直径[m]
ファニングの式はポンプの揚程を計算する際に、直管の圧力損失を計算するのに使用されます。

ベルヌーイの定理の記事で解説した、摩擦損失水頭hfはファニングの式の圧力損失ΔPから計算できます。
$$h_{f}=\frac{ΔP}{ρg}・・・(2)$$
上の(2)式によりΔP(圧力)からhfのヘッド(長さ)の単位へと変換できます。
もしファニングの式で圧力損失を考慮せずに実揚程だけでポンプの揚程を決めてしまうと、流体と配管との摩擦によりエネルギーが損失するため、目的の場所まで流体を送ることができなくなります。
したがって圧力損失をちゃんと計算し、摩擦によるエネルギー損失分を上乗せしてポンプの揚程を決める必要があります。
ファニングの式の導出
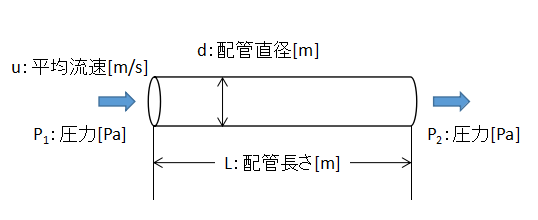
上図に示すような配管流れを考えます。
流体は平均流速uで配管内を流れているとします。
このとき、流体は粘性により壁面に力Fを及ぼしますが、この力Fは摩擦係数fを定数として、
$$F=f・(πdL)・\frac{1}{2}ρu^{2}・・・(3)$$
(3)式で表されます。
また、配管長さLの区間での圧力降下による力の損失FLは、
$$F_{L}=\frac{πd^{2}}{4}(P_{1}-P_{2})=\frac{πd^{2}}{4}ΔP・・・(4)$$
(4)式となります。
流体が壁面に及ぼす力Fとこの区間での力の損失FLは等しいので(3)式=(4)式となります。
$$f・(πdL)・\frac{1}{2}ρu^{2}=\frac{πd^{2}}{4}ΔP$$
$$ΔP=4f\frac{ρu^{2}}{2}\frac{L}{d}・・・(1)$$
式変形すると冒頭の(1)式となり、ファニングの式を導くことができました。
摩擦係数fの使い分け
実務としては摩擦係数fをどのような値として計算するかが重要です。
流体の摩擦度合いを表わす摩擦係数fは、流れの状態(層流、乱流)や配管壁面のざらざら度合いによって値が変わることは想像できます。
そこで、様々な条件下での摩擦係数を求める式が発表されています。
その中でも簡便に計算できるのが、下の2式です。
・層流(Re≦2,000)
$$f=\frac{16}{Re}$$
・乱流(3,000≦Re≦100,000)
$$f=0.0791Re^{-0.25}$$
また、摩擦係数の様々な実験結果をプロットしたムーディ図から摩擦係数の値を読み取り使用するのも1つの方法です。
下図にムーディ線図を示します。
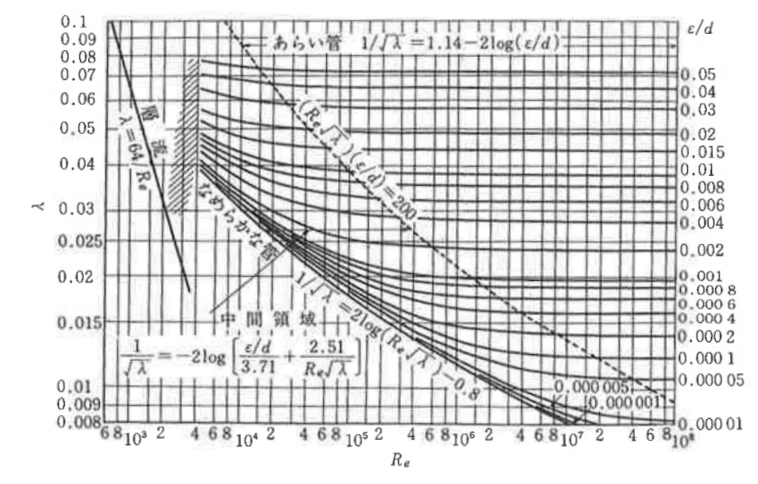
ただし、注意点としてムーディ線図は機械工学の分野で使用されることが多く、摩擦係数fではなくλが縦軸にプロットしてあることが多いです。
機械工学の分野ではファニングの式と同様の意味合いの式としてダルシー・ワイズバッハの式が存在します。
$$h_{f}=\frac{ΔP}{ρg}=λ\frac{u^{2}}{2g}\frac{L}{d}・・・(5)$$
(5)式がダルシー・ワイズバッハの式です。
ファニングの式である(1)式を(2)式に代入すると、
$$h_{f}=4f\frac{u^{2}}{2g}\frac{L}{d}・・・(6)$$
(6)式となり(5)式とほぼ同じ形となります。
(5)式と(6)式を比較すると、
$$λ=4f・・・(7)$$
(7)式となることがわかります。
したがって、ムーディ線図から読み取ったλを4で割れば摩擦係数fになります。
忘れずに変換しましょう。
