概要
この記事では熱交換器のシェル側を流れる流体の境膜伝熱係数についてまとめています。
配管内の流動と比べるとやや複雑な流れになりますが、種々のパラメータで補正をかけることでうまく相関できる式がいくつか発表されています。
各推算式
バッフルがない場合
Shortの式
シェル内にバッフルがあるかどうかで流体の流動状態は大きく変わります。
バッフルが無い場合にはShortの式が提案されています。
$$Nu=\frac{h_{o}D_{i}}{λ}=0.16Re^{0.6}Pr^{0.33}(\frac{μ}{μ_{w}})^{0.14}$$
適用範囲
$$200≦Re≦20,000$$
Nu:ヌセルト数[-]、ho:シェル側境膜伝熱係数[W/(m2K)]、Di:伝熱管内径[m]、
λ:流体の熱伝導度[W/mK]、Re:レイノルズ数[-]、Pr:プラントル数[-]
"熱交換器設計ハンドブック, 尾花英明,(2000)"を参照
注意点としてはレイノルズ数を求めるときは管束部を流れる流体の流量から求めるべき、ということです。
管束部の外側を流れる流体は伝熱には寄与していませんので正味の流量は少し減少します。
ところで、実務ではバッフルが1枚も入っていない熱交換器はあまり見かけません。
理由は二つあり、
・バッフルがないと流体が素通りしてしまい境膜伝熱係数が悪化するため。
・バッフルは伝熱管を固定する役割もあり振動防止効果があるため、バッフルがないと振動しやすくなるため。
といったことが挙げられます。
バッフルがある場合
Kernの式
$$Nu=\frac{h_{o}D_{e}}{λ}=j_{H}Pr^{\frac{1}{3}}(\frac{μ}{μ_{w}})^{0.14}$$
Nu:ヌセルト数[-]、ho:シェル側境膜伝熱係数[W/(m2K)]、De:相当管径[m]、
λ:流体の熱伝導度[W/mK]、jH:因子[-]、Pr:プラントル数[-]
μ:流体粘度[cp]、μw:壁面での流体粘度[cp]
"熱交換器設計ハンドブック, 尾花英明 ,(1999)"を参照
管内境膜伝熱係数の相関式でjH因子を読み取って算出する式がありましたが、シェル側の境膜伝熱係数でも似たような式があります。
Deは相当直径で、伝熱管の配置によって求める式が変わります。
4角配置のときは
$$De=\frac{4(P_{t}^{2}-πD_{o}^{2}/4)}{πD_{o}}$$
3角配置のときは
$$De=\frac{4[(0.5P_{t})(0.86P_{t})-0.5πD_{o}^{2}/4]}{πD_{o}/2}$$
となります。
jH因子は下の計算図表から読み取った値を使用します。
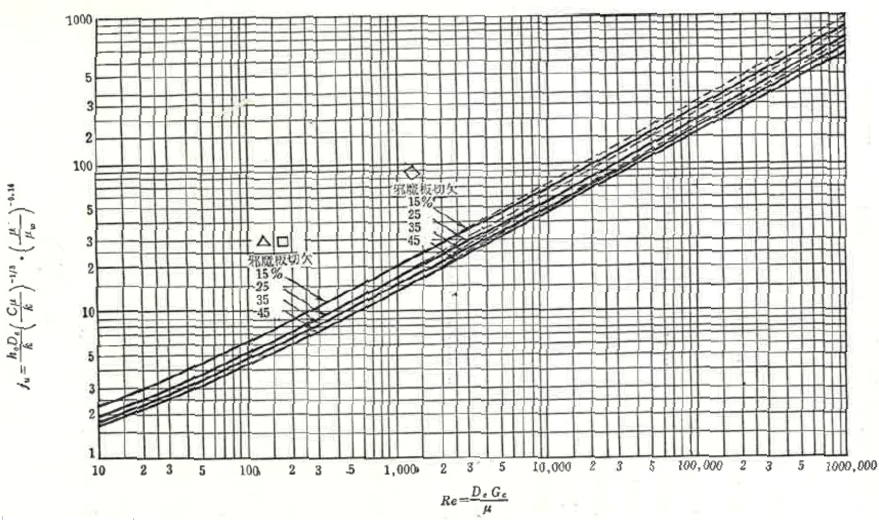
後述するBellの式と比べると簡単で使いやすい式です。
Bellの式
$$h_{o}=F_{fh}j_{h}(CG_{c})Pr^{-\frac{2}{3}}(\frac{μ}{μ_{w}})^{0.14}(\frac{φξ_{h}}{X})F_{g}$$
ho:シェル側境膜伝熱係数[W/(m2K)]、Ffh:管種による補正係数[m]、jh:因子[-]
Gc:熱交換器の中心線に最も近い管列での直交流れの最大質量速度[kg/(m2 h)]
C:流体の比熱[J/(kg K)]、Pr:プラントル数[-]
μ:流体粘度[cp]、μw:壁面での流体粘度[cp]
φ:バッフル切欠部を通る流れによる補正係数
ξh:シェルと管束の間を通る流れによる補正係数
X:管列数による補正係数
Fg:バッフル管穴と伝熱管のすき間を通る流れによる補正係数
"熱交換器設計ハンドブック, 尾花英明 ,(1999)"を参照
Kernの式よりも精度が良いと言われているのがこのBellの式です。
バッフルがあることによりシェル内の流れが複雑化しますが、各々の流れに関して補正係数を求めています。
補正係数の算出に関して詳しく知りたい方は"熱交換器設計ハンドブック"を参照してみてください。
生産技術職の方は職場に置いてあることも多いかと思います。
各式の計算比較
バッフル有りの計算式であるKernの式、Bellの式とaspentech社がリリースしている熱交換器設計ソフト"Aspen Exchanger Design and Rating"(以下EDR)で試しに計算してシェル側境膜伝熱係数を比較してみました。
シェル径350mm、伝熱管外径25.4m、チューブ本数85本の多管式熱交換器をモデルとし、冷却水をシェル側に流して、冷却水流量を変化させて計算しました。
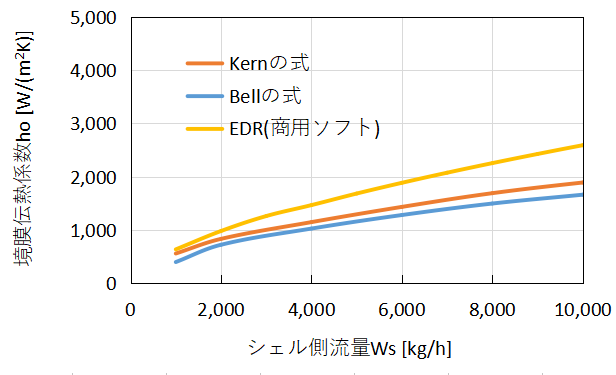
上のグラフに結果を示します。
どの計算手法でも傾向としては同じで、シェル側流量が多くなるほど境膜伝熱係数が増加しています。
Kernの式とBellの式は比較的近い値を示しています。
計算する前はBellの式とEDR結果が近い値となることを想定していましたが、残念ながら今回の計算条件ではそうなりませんでした。
一方でEDRの結果は境膜伝熱係数が少し大きめに出る結果となりました。
EDRの場合はより細かく熱交換器内のパーツについて情報を入力していることから、部分的に縮流となる箇所が多く、冷却水流速が増加し境膜伝熱係数が高くなったものと推察されます。
