概要
この記事では気体密度の推算方法をおおまかに2種類に分けて紹介します。
・状態方程式による方法
・一般化圧縮係数線図による方法
どちらの手法も一長一短あり、あらゆる面で最も優れている手法というものはありません。
この手の推算方法の常ですが、簡便に求められるものは推算精度があまり良くなく、逆に精度が良いものはそのぶん補正係数の式が複雑で計算に必要なパラメータも多くなる傾向にあります。
化学工学的には気体密度がわかっていなければ計算・検討できないことがほとんどですので、何かしらの手法で気体密度は算出する必要があります。
しかし必要とされる精度に関しては装置の種類や目的によって様々です。
例えば排ガスの吸収塔は気液平衡の精度さえ高ければ、密度のデータに関してはそこまでの精度を要求されないイメージです。
一方でプロセスの主要成分を分離する蒸留塔は、気液平衡の精度はもちろんのこと気体密度の精度も重要になってきます。
商用のシミュレーターを使用している場合でもどのような推算式を使用しているのかは確認しておくべきでしょう。
気体密度の実測値
参考までに0℃、1atmにおける主要な気体密度を示します。
だいたいどのくらいのオーダーになるのか知っておけば、推算式で単位換算ミスに気づきやすくなります。
| 物質 | 密度[kg/m3] | 物質 | 密度[kg/m3] |
| アセチレン | 1.1708 | シラン | 1.44 |
| アルゴン | 1.7828 | 水素 | 0.0898 |
| アンモニア | 0.7710 | 窒素 | 1.2507 |
| 一酸化炭素 | 1.2501 | 二酸化硫黄 | 2.9269 |
| 一酸化窒素 | 1.3402 | 二酸化炭素 | 1.9769 |
| 一酸化二窒素 | 1.9778 | ネオン | 0.9002 |
| エタン | 1.3567 | ブタン | 2.5985 |
| エチレン | 1.2644 | フッ化ケイ素 | 4.684 |
| 塩化エチル | 2.2198 | フッ化水素 | 0.9218 |
| 塩化水素 | 1.6392 | フッ素 | 1.6354 |
| 塩化ニトロシル | 2.992 | フレオン-22 | 2.3044 |
| 塩化メチル | 1.7823 | プロパン | 2.0200 |
| 塩素 | 3.214 | ヘリウム | 0.1785 |
| キセノン | 5.896 | ホスゲン | 4.5313 |
| Air | 1.2929 | ホスフィン | 1.5293 |
| クリプトン | 3.739 | メタン | 0.7167 |
| 酸素 | 1.4289 | メチルエーテル | 2.091 |
| シアン | 2.3348 | ヨウ化水素 | 5.7891 |
| 臭化水素 | 3.6445 | 硫化水素 | 1.5392 |
| 臭素 | 7.1338 |
純物質の気体密度推算
状態方程式による推算法と一般化圧縮係数線図による推算法を紹介します。
比較として各手法でイソブタン(C4H10)の30atm、410Kにおける気体密度を推算してみます。
ちなみに実測値は0.0850g/cm3です。
状態方程式による気体密度推算
様々な状態方程式のモデルが提案されていまして、そのうちの一部を紹介します。
理想気体の状態方程式
理想気体に近い条件下ではこの方法で密度を推算することができます。
$$PV=RT$$
$$ρ=\frac{M}{V}$$
$$ρ=\frac{MP}{RT}$$
P:圧力[atm]、V:体積[cm3]、T:温度[K]、R:気体定数[(atm cm3)/(mol K)]
ρ:密度[g/cm3]、M:分子量[g/mol]
しかし高圧条件下では非理想性が強くなり、ズレが大きくなります。
試しにイソブタンの気体密度を推算してみましょう。30atmと高圧条件なので精度が悪いことが予想されます。
イソブタンの分子量はM=58.1ですので、
$$ρ=\frac{MP}{RT}=\frac{58.1×30}{82.06×410}=0.0518g/cm^{3}$$
となります。実測値が0.0850g/cm3なのでかなりずれていますね。
ファン・デル・ワールス式
実在気体向けの状態方程式の中では最も簡潔な式です。
$$(P+\frac{a}{V^{2}})(V-b)=RT$$
P:圧力、V:体積、T:温度、R:気体定数、a、b:物質に固有な定数
圧力項に分子間力の影響を考慮しa/V2を追加し、体積項を分子の占める体積で引くことでV-bとし修正しています。
この式を使用して密度を求める際には、臨界定数を利用します。
臨界点において定数a、bを臨界温度Tc、臨界圧力Pcで表すと、
$$a=\frac{27}{64}\frac{R^{2}T_{c}^{2}}{P_{c}}$$
$$b=\frac{R^{2}T_{c}}{8P_{c}}$$
となります。
また、最初のファン・デル・ワールス式を体積Vについて整理すると
$$V^{3}-(\frac{RT}{P})V^{2}+\frac{a}{P}V-\frac{ab}{P}=0$$
となります。
両辺に(P/RT)3をかけると
$$(\frac{P^{3}}{R^{3}T^{3}})V^{3}-(\frac{P^{2}}{R^{2}T^{2}}+\frac{P^{3}b}{R^{3}T^{3}})V^{2}+\frac{aP^{2}}{R^{3}T^{3}}V-\frac{abP^{2}}{R^{3}T^{3}}=0$$
となります。
ここで圧縮係数zを利用して、
$$z=\frac{PV}{RT}$$
$$A=\frac{aP}{R^{2}T^{2}}$$
$$B=\frac{bP}{RT}$$
とおいて整理すると、
$$z^{3}-(1+B)z^{2}+AZ-AB=0$$
というzに関する3次方程式になります。
この方程式を解けばzが得られ、
$$ρ=\frac{MP}{zRT}$$
上式から気体密度がわかります。
3次方程式は解析解があるようですが、非常に複雑なのでエクセルのソルバー等を利用して近似解を求める方が簡単だと思います。
この式でも試しにイソブタンの気体密度を推算してみましょう。
イソブタンの臨界温度Tc=408.1K、臨界圧力Pc=36.0atmなので、
$$a=\frac{27}{64}\frac{R^{2}T_{c}^{2}}{P_{c}}=\frac{27×82.06^{2}×408.1^{2}}{64×36.0}=13.1×10^{6}$$
$$b=\frac{R^{2}T_{c}}{8P_{c}}=\frac{82.06×408.1}{8×36.0}=116.3$$
a、bが求められます。
a、bを利用してさらにA、Bを求めます。
$$A=\frac{aP}{R^{2}T^{2}}=\frac{13.1×10^{6}×30}{82.06×410}=0.348$$
$$B=\frac{bP}{RT}=\frac{116.3×30}{82.06×410}=0.104$$
zの3次方程式にA、Bを代入して、
$$z^{3}-1.103z^{2}+0.348Z-0.0361=0$$
エクセルのソルバーで解くと、z=0.657のときに左辺≒0となり収束しました。
よって
$$ρ=\frac{58.1×30}{0.657×82.06×410}=0.0788g/cm^{3}$$
となりました。実測値が0.0850g/cm3なので理想気体の状態方程式よりは精度が上がっていますね。
Redlich-Kwong式(RK式)
ファン・デル・ワールス式で多少精度は上がりましたが、まだまだ精度が良いとは言えません。
その後ファン・デル・ワールス式をベースとした様々な修正式が提案されました。
本記事ではその中の一つであるRedlich-Kwong式(以下RK式)を紹介します。
このあたりのモデルから実務レベルで使用されている精度になってきます。
$$P=\frac{RT}{V-b}-\frac{a}{T^{0.5}V(V+b)}$$
P:圧力、V:体積、T:温度、R:気体定数、a、b:物質に固有な定数
上式にRK式を示します。
ファン・デル・ワールス式の分子間力にさらに補正をかけた式となっています。
ファン・デル・ワールス式と同様に密度を求める際には、臨界定数を利用します。
臨界点において定数a、bを臨界温度Tc、臨界圧力Pcで表すと、
$$a=\frac{Ω_{a}R^{2}T_{c}^{2.5}}{P_{c}}$$
$$b=\frac{Ω_{b}RT_{c}}{P_{c}}$$
$$Ω_{a}=0.42748$$
$$Ω_{b}=0.086640$$
となります。
続いて同様に圧縮係数zに関して整理します。
ファン・デル・ワールス式と比較して少し導出が長くなってしまうのでここでは省略します。
結果として、
$$A=\frac{aP}{R^{2}T^{2.5}}$$
$$B=\frac{bP}{RT}$$
$$z^{3}-z^{2}+(A-B-B^{2})Z-AB=0$$
となりまして、得られた圧縮因子zから密度を算出できます。
同様にイソブタンの気体密度を推算してみましょう。
イソブタンの臨界温度Tc=408.1K、臨界圧力Pc=36.0atmなので、
$$a=\frac{0.042748×82.06^{2}×408.1^{2.5}}{36}=2.69×10^{7}$$
$$b=\frac{0.086640×82.06×408.1}{36}=80.60$$
a、bが求められます。
a、bを利用してさらにA、Bを求めます。
$$A=\frac{2.67×10^{7}×30}{82.06^{2}410^{2.5}}=0.352$$
$$B=\frac{80.60×30}{82.06×410}=0.0719$$
zの3次方程式にA、Bを代入して、
$$z^{3}-z^{2}+0.275Z-0.0361-0.0253=0$$
エクセルのソルバーで解くと、z=0.624のときに左辺≒0となり収束しました。
よって
$$ρ=\frac{58.1×30}{0.624×82.06×410}=0.0830g/cm^{3}$$
となりました。実測値が0.0850g/cm3なのでかなり精度が上がっていますね。
実務ではこのRKモデルをさらに修正したSRKモデルのような、より精度の高いモデルを使用することも当然あります。
紹介しだすときりがないのでこの記事ではここまでにします。
また別の記事で状態方程式についてはまとめるかもしれません。
一般化圧縮係数線図による気体密度推算
圧縮係数を対臨界定数で一般化した線図を利用して密度を推算することができます。
線図から読み取る作業はいりますが複雑な計算がなく、なおかつ精度も良いのが特徴です。
同様にイソブタンの気体密度を推算してみましょう。
イソブタンの臨界温度Tc=408.1K、臨界圧力Pc=36.0atmなので、
$$T_{r}=\frac{410}{408.1}=1.005$$
$$P_{r}=\frac{30}{36}=0.833$$
求めた対臨界温度Tr、対臨界圧力Prの値で線図からzを読み取ります。
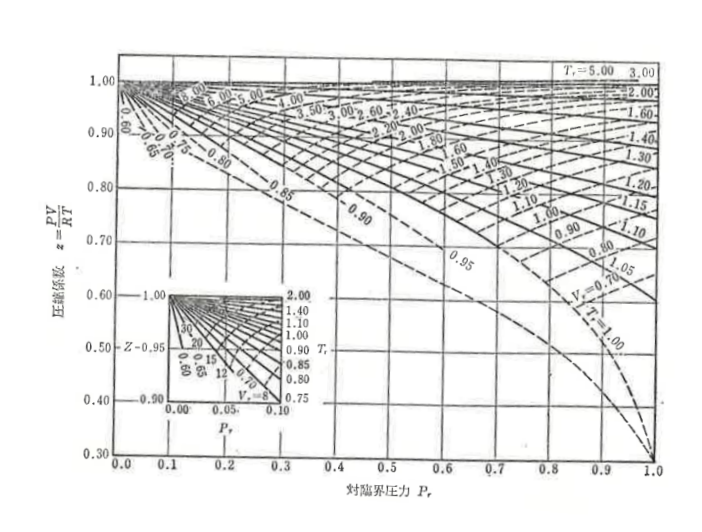
z=0.605と読み取りました。
よって、
$$ρ=\frac{58.1×30}{0.605×82.06×410}=0.0788g/cm^{3}=0.0856g/cm^{3}$$
となりました。実測値が0.0850g/cm3なのでかなり精度が良いですね。
ただし実務ではいちいち線図を読み取るのは時間がかかるため、定式化されている状態方程式モデルを使用することが多いかと思います。
混合物の気体密度推算
状態方程式による気体密度推算
平均分子量の利用
超概算レベルの計算では単純に平均分子量Mmから混合物の密度を算出することもあります。
$$M_{m}=\sum_{j}x_{j}M_{j}$$
$$ρ=\frac{M_{m}P}{RT}$$
物理化学や熱力学のテストではよく使うかもしれません。
実務においては気体密度の推算にはあまり使われません。
なぜなら状態方程式モデルや一般化圧縮係数線図が混合物にも適用できるからです。
ファン・デル・ワールス式
気体は分子間距離が大きいため、異種分子が混入しても分子間の相互作用にはほとんど影響を与えません。
そのため純物質の推算方法が混合物にも使用できます。
ただし臨界定数は純物質ではなく混合物の値を使用する必要があります。
Redlich-Kwong式(RK式)
同様に臨界定数は純物質ではなく混合物の値を使用する必要があります。
加えて定数a、bの算出方法が混合物を加味した式に変わります。
$$P=\frac{RT}{V-b_{m}}-\frac{a_{m}}{T^{0.5}V(V+b_{m})}$$
定数a、bのところをam、bmに変え、
$$a_{m}=(\sum_{i}x_{i}\sqrt{a_{i}})^{2}$$
$$b_{m}=\sum_{i}x_{i}b_{i}$$
$$a_{i}=\frac{Ω_{a}R^{2}T_{c}^{2.5}}{P_{c}}$$
$$b_{i}=\frac{Ω_{b}RT_{c}}{P_{c}}$$
$$Ω_{a}=0.42748$$
$$Ω_{b}=0.086640$$
となります。
それぞれの物質についてa、bを求めてam、bmを算出します。
その後は同様に圧縮係数zについての方程式を解けば、混合密度を算出できます。
一般化圧縮係数線図による気体密度推算
同様に臨界定数は純物質ではなく混合物の値を使用する必要がありますが、やることは変わりません。
線図から圧縮係数zを読み取り計算するだけです。
