概要
粒子が流体中を沈降する場合に、重力と抗力が釣り合い加速度がゼロになったときの沈降速度を終末速度(あるいは終端速度、終末沈降速度)といいます。
流体中から粒子を分離する操作(固液分離、気液分離)においては、粒子の終末速度が重要な因子となることがあります。
本記事では終末速度の算出方法について解説します。
粒子の運動方程式
粒子の終末速度は、粒子に働く力の釣り合いを考えることで導出されます。
ニュートンの運動方程式ma=Fを粒子に適用させると、
$$m\frac{dv}{dt}=\frac{π}{6}ρ_{p}g{d_{p}}^{3}-(\frac{π}{6}ρg{d_{p}}^{3}+C_{d}・\frac{π{d_{p}}^2}{4}・\frac{ρv^2}{2})・・・(1)$$
m:粒子の質量[kg]、v:粒子の沈降速度[m/s]、dp:粒子径[m]
ρp:粒子密度[kg/m3]、ρ:流体密度[kg/m3]、g:重力加速度[m/s2]、Cd:抵抗係数[-]
(1)式となります。
右辺第一項が粒子の受ける重力、第二項が粒子の受ける浮力、第三項が粒子の受ける抵抗力となります。
粒子は沈降直後は重力により加速しますが、やがて第一項の重力と第二項、第三項で表される抗力が釣り合うようになります。
このとき、左辺のdv/dt=0となるので、
$$0=\frac{π}{6}ρ_{p}g{d_{p}}^{3}-(\frac{π}{6}ρg{d_{p}}^{3}+C_{d}・\frac{π{d_{p}}^2}{4}・\frac{ρ{v_{t}}^2}{2})・・・(2)$$
(2)式となります。(2)式を整理すると、
$$v_{t}=\sqrt{\frac{4(ρ_{p}-ρ)gd_{p}}{3ρC_{d}}}・・・(3)$$
vt:終末速度[m/s]
(3)式となります。
(3)式が終末速度vtを算出する一般式となります。
抵抗係数Cdの算出
(3)式から、抵抗係数Cdがわかれば終末速度vtを求めることができます。
抵抗係数Cdは粒子の大きさによって相関が大きく変化します。
一般には(4)式で表される粒子レイノルズ数Reによって整理されます。
$$Re=\frac{ρvd_{p}}{μ}・・・(4)$$
μ:流体粘度[Pa・s]
ここでは、提唱されている抵抗係数Cdの計算式の一部を紹介します。
Stokes領域
Re<2のとき、抵抗係数Cdは
$$C_{d}=\frac{24}{Re}・・・(5)$$
(5)式で近似して表されます。
(5)式を(3)式に代入すると、
$$v_{t}=\sqrt{\frac{4(ρ_{p}-ρ)gd_{p}・ρv_{t}d_{p}}{3ρ・24μ}}$$
$$v_{t}=\frac{(ρ_{p}-ρ)g{d_{p}}^2}{18μ}・・・(6)$$
(6)式となります。(6)式をStokesの式、あるいはStokes則といいます。
Stokes則は一般に微細な粒子に対して成り立ち、粒子の周りの流れは層流となります。
実際に(5)式の抵抗係数と実測値を比較したグラフを以下に示します。
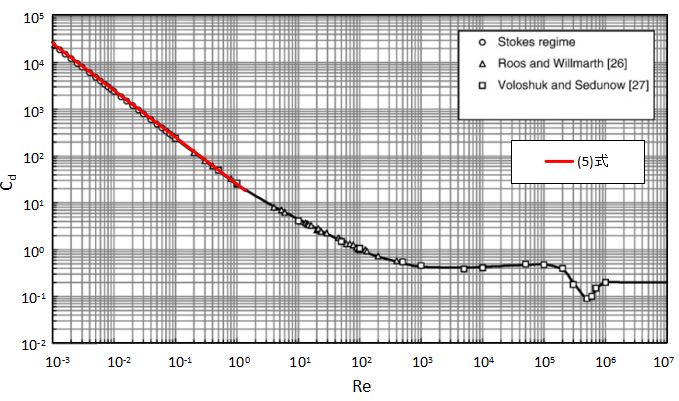
Re<2の範囲では(5)式が良好に一致することがわかります。
中間領域
2<Re<500のとき、抵抗係数Cdは
$$C_{d}=\frac{18.5}{Re^0.6}・・・(7)$$
(7)式で近似して表されます。
(7)式をAllenの式といい、粒子の周りの流れが層流と乱流の間の中間領域(遷移領域)でよく一致します。
(7)式の抵抗係数と実測値を比較したグラフを以下に示します。
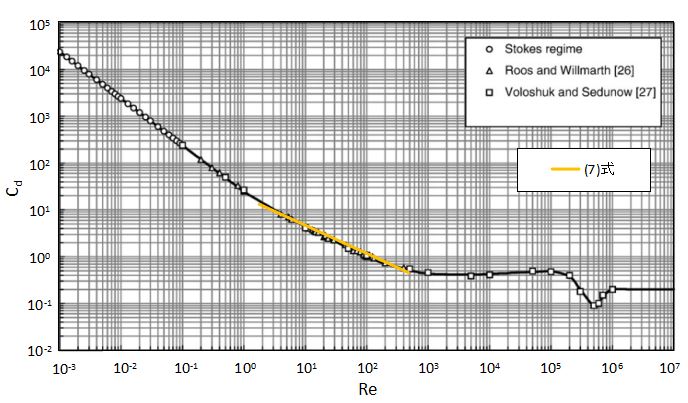
2<Re<500の範囲では(5)式が良好に一致することがわかります。
Newton領域
500<Re<105のとき、粒子の周りの流れは乱流となります。
この領域をNewton領域といい、抵抗係数Cdは
$$C_{d}=0.44・・・(8)$$
(8)式のように一定値で表されます。
(8)式の抵抗係数と実測値を比較したグラフを以下に示します。
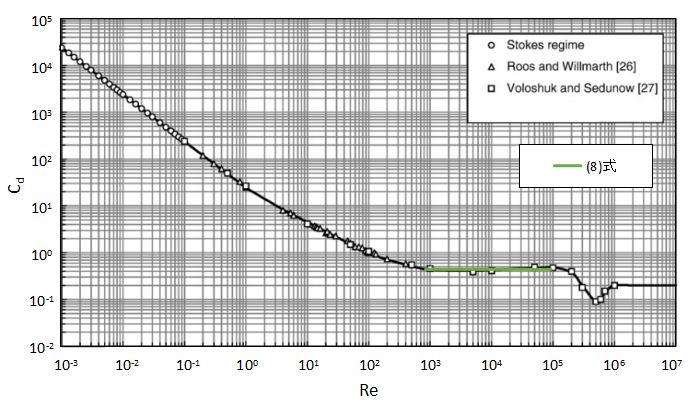
Newton領域ではの範囲では(8)式が良好に一致することがわかります。
臨界領域
Newton領域からさらに粒子レイノルズ数が増加すると、乱流剥離が発生し抗力が低下します。
この臨界領域における抵抗係数Cdは、
$$\begin{align}C_{d}&=\frac{24}{Re}+\frac{2.6・(Re/5.0)}{1+(Re/5.0)^{1.52}}+\frac{0.411・[Re/(2.63×10^5)]^{-7.94}}{1+[Re/(2.63×10^5)]^{-8.0}}\\&+\frac{0.25・(Re/10^6)}{1+(Re/10^6)}・・・(9)\end{align}$$
(9)式のMorrison式が比較的よく一致します。
(9)式の抵抗係数と実測値を比較したグラフを以下に示します。
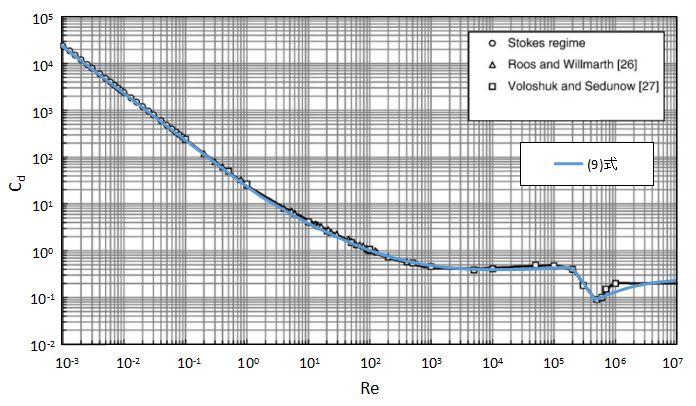
上図から、Morrison式はStokes領域、中間領域、Newton領域でも比較的よい精度で計算できるため、汎用性が高いです。
まとめ
粒子の終末速度について解説しました。
粒子の大きさにより相関が大きく変化するため、系によって式を使い分けましょう。
