概要
Secant法(割線法)は非線形方程式を解く手法の1つです。
Newton-Raphson法に近い計算手法であるため、準ニュートン法(quasi-Newton method)とも呼ばれています。
Aspen Plusなどの化工計算シミュレータに採用されている収束計算手法であり、バリバリ化工計算をする人にとっては使用頻度も高いでしょう。
原理
方程式f(x)=0の解を求めることを考えます。
Newton-Raphson法では、
$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}・・・(1)$$
(1)式のようにf(x)の微分f'(x)を使用して次のステップを計算します。
詳しくは下の記事で解説しています。

これに対してSecant法では、
$$f'(x_{n})≒\frac{f(x_{n})-f(x_{n-1})}{x_{n}-x_{n-1}}・・・(2)$$
(2)式のように微分の代わりに近似値を使用します。そのため、
$$x_{n+1}=x_{n}-\frac{x_{n}-x_{n-1}}{f(x_{n})-f(x_{n-1})}f(x_{n})・・・(3)$$
(3)式を使用して次のステップを計算します。これがSecant法の計算手法です。
ポイントとしては、初期値を2つ設定する必要がある点です。
他の収束計算手法と共通しますが、解から遠い値を初期値として設定してしまうと収束しなくなったり遅くなったりするので、ある程度近い初期値を設定したいところです。
また、Newton法と違って近似値を使用しているぶん、計算誤差が若干大きくなる可能性があります。Secant法でどうしても収束しないようならNewton法に切り替えるのもありです。
表計算ソフト計算例
実際にSecant法を使って表計算ソフトで計算してみましょう。
Underwoodの式
ここでは例として、Underwoodの式を使って蒸留塔の最小還流比を求めてみましょう。
Underwoodの式は、
$$R_{m}=k\sum_{i=1}^{n}(\frac{x_{iD}}{k-α_{1i}})-1・・・(4)$$
Rm:最小還流比[-]、k:定数、xiD:留出液中の成分i組成[-]
α1i:成分1の成分iに対する相対揮発度[-]
(4)式で表されます。
また、定数kは
$$\sum_{i=1}^{n}(\frac{x_{iF}}{k-α_{1i}})=\frac{1-q}{k}・・・(5)$$
xiF:フィード中の成分i組成[-]、q:原料の予熱状態
(5)式から算出することができます。
蒸留塔での分離条件ですが、
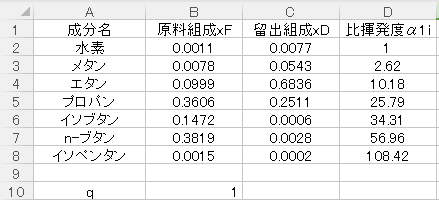
| 成分i | 原料組成xiF | 留出物組成xiD | 相対揮発度α1i |
| 水素 | 0.0011 | 0.0077 | 1.00 |
| メタン | 0.0078 | 0.0543 | 2.62 |
| エタン | 0.0999 | 0.6836 | 10.18 |
| プロパン | 0.3606 | 0.2511 | 25.79 |
| イソブタン | 0.1472 | 0.0006 | 34.31 |
| n-ブタン | 0.3819 | 0.0028 | 56.96 |
| イソペンタン | 0.0015 | 0.0002 | 108.42 |
上の表に示す条件とします。
また、今回はq=1として計算してみます。
Secant法での計算
(5)式をf(k)=0の形に変形すると、
$$f(k)=\sum_{i=1}^{n}(\frac{x_{iF}}{k-α_{1i}})-\frac{1-q}{k}・・・(6)$$
(6)式となります。
この(6)式をSecant法で解くことになります。
まずは前提条件を下図のようにセルに入力します。
続いて(6)式の計算式をセルに入力していきます。
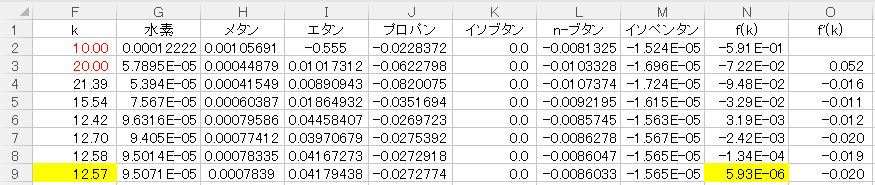
まず2つの初期値をF2セル、F3セルに入力します。試行錯誤でうまく収束するような初期値を選びましょう。今回はk=10,20と入力しました。
次に、(6)式中のxiF/(k-α1i)を各成分G2セル~M2セルに入力します。xiFとα1iは値が動かないようにF4キーで固定し、G3セル~M3セルにコピーして貼り付けます。
次に、f(k)の値を(6)式をもとにN2セルに入力します。定数k以外の値は同様にF4キーで固定しましょう。その後、N2セルをN3セルに貼り付けます。
次に、f'(k)の値を(2)式をもとに計算します。
$$O3セル=\frac{N3セル-N2セル}{F3セル-F2セル}・・・(7)$$
O3セルには(7)式のように入力します。
あとは、F3セル~O3セルまでを定数kの収束解が得られるまで下にコピーしていくだけです。
今回は|f(k)|≦10-4となれば収束したと判定しています。
9行目においてf(k)=5.93E-6となり、そのときk=12.57となりました。
最後に(4)式を使用して最小還流比Rmを計算します。
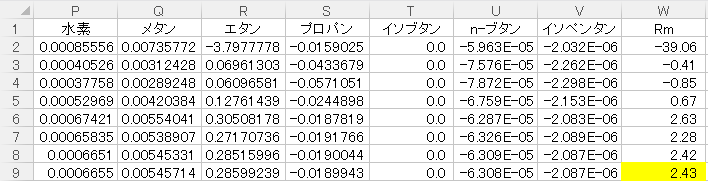
上図に示すように(4)式中のxiD/(k-α1i)を各成分P2~V2に入力します。その後、W2セルに(4)式からRmを入力します。
あとは定数kで収束計算した行までコピーして貼り付けるだけです。
計算の結果、最小還流比Rmは2.43となりました。
まとめ
非線形方程式を解く手法の1つであるSecant法について解説しました。
実務でもよく使用される収束計算手法なので覚えておくとよいでしょう。
