概要
本記事ではPythonでの化学工学計算例を紹介しています。今回はNewton-Raphson法を使用して、対数平均温度差を含む熱収支を計算します。
主に熱交換器の設計をする際に計算する式で、実務でもよく登場します。
化学工学シミュレータを使用すればあっという間に解けるような式ですが、Pythonでいちから式を立てると意外に解けなくて苦戦することがあるかもしれません。
本記事ではプログラミング系の言語を今まで触ったことがない人をターゲットとし、自分が躓いたところを中心になるべく基礎的なところから解説しています。
逆に化学工学の計算式についてはある程度理解のあるものとし、解説は適宜割愛します。ご容赦ください。
計算式
今回計算する式は以下の記事で解説したものを使用します。
上の記事ではExcelを使用してNewton-Raphson法で解いていますが、今回は同じ式をPythonで解いてみます。
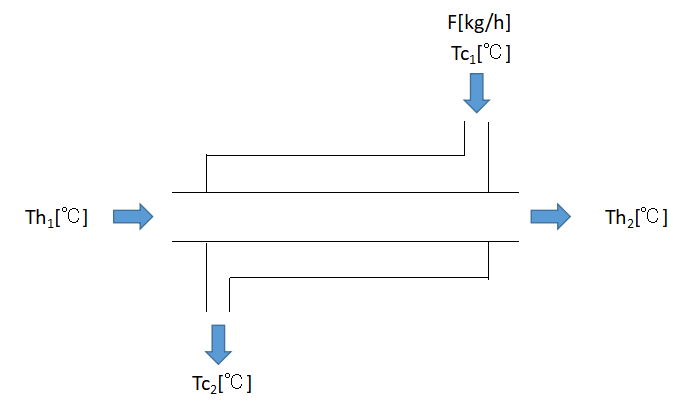
- 低温側流体流量F:45,000kg/h
- 低温側流体比熱Cp:1.0kcal/(kg・℃)
- 熱交換器の総括伝熱係数U:550kcal/(m2・h・℃)
- 熱交換器の伝熱面積A:20m2
- 高温側流体の入口温度Th1:78℃
- 低温側流体の入口温度Tc1:31℃
- 低温側流体の出口温度Tc2:38℃
$$f(Th2)=FCp(Tc2-Tc1)-UA\frac{(Th1-Tc2)-(Th2-Tc1)}{{\rm{ln}}(\frac{Th1-Tc2}{Th2-Tc1})}・・・(1)$$
前提条件と計算式は上に示す通りです。
(1)式がf(Th2)=0となるようなTh2をNewton-Raphson法で求めます。
ちゃんと計算できていれば、Th2=50.66℃になるはずです。
新しい計算ソフトに手を出すときは、本記事のようにとりあえず答えのわかる問題から解くのが良いと思います。
Python記述
ライブラリ・モジュールのインポート
まず最初に使用するライブラリやモジュールをインポートします。
今回はmathモジュールを使用します。対数平均温度差の項を計算するためにlogの値を計算する必要があるからです。
Excelではlogとかlnと打てば対数計算できますが、Pythonではモジュールを最初にインポートしないと計算できません。
#mathモジュールインポート
import math前提条件の入力
次に問題で与えられる前提条件を入力します。
#前提条件
F=45000 # kg/h
Cp=1 # kcal/(kg・℃)
U=550 # kcal/(m2・h・℃)
A=20 # m2
Th1=78 # ℃
Tc1=31 # ℃
Tc2=38 # ℃念のためコメントで単位を付けておくと、後から見たときに単位変換ミスに気づきやすくてよいです。
初期条件の入力
次に初期条件が必要な場合はその値を入力します。
今回はNewton-Raphson法を使用するためTh2の初期値が必要ですね。
#初期条件
Th20=40 # ℃Th20=40℃と設定します。
その他計算条件の入力
今回はざっくりとその他計算条件でまとめました。もう少し細かく分類できる場合は分けた方がよいかもしれません。
f(Th2)の微分を求める際に温度刻みΔTが必要なのでその値を入力します。
#その他計算条件
ΔT=0.001方程式の定義
次にメインの方程式を定義します。
定義の記述の仕方も様々あるようですが、今回はdefとreturnで関数を定義します。
#方程式定義
def fTh2(Th2):
return F*Cp*(Tc2-Tc1)-U*A*((Th1-Tc2)-(Th2-Tc1))/math.log((Th1-Tc2)/(Th2-Tc1)) #(1)式定義
def dfTh2(Th2):
return (fTh2(Th2+ΔT)-fTh2(Th2))/ΔT #(2)式定義2,3行目で(1)式を定義しています。対数については、math.log()と記述することでeが底の対数を計算できます。
defでfTh2(Th2)という関数を定義し、3行目のreturn文で式を入力します。こうすることで以降の記述でfTh2(Th2)と記載すると、return文に入力した式を計算して値を返してくれます。
fTh2(Th2)の括弧内のTh2は数学で言うところの変数(プログラミング用語では引数と呼ばれます)で、様々な値を入力することができます。
今回のようにTh2の初期値が40℃から始まり、繰り返し計算でTh2の値が変わっていくような計算ではよく使用します。
5,6行目でf(Th2)の微分f'(Th2)を定義しています。
(1)式が簡単に微分可能であれば微分すればよいですが、今回は難しそうですね。その場合には数値微分の形でf(Th2)を算出します。
$$f'(Th2(n+1))=\frac{f(Th2(n)+ΔT)-f(Th2(n))}{ΔT}・・・(2)$$
こちらの記事で解説していますが、(2)式が数値微分した式になります。前進Euler法を使用しています。
5,6行目に(2)式をdefで定義してメインの方程式定義は終了です。
Newton-Raphson法の入力
続いてNewton-Raphson法の収束計算式を入力していきます。
今回はdefで収束計算式を定義し、while文で繰り返し計算を行ないます。
#Newton-Raphson法
def newton(Th20):
n=1 #計算回数初期値
error=1 #エラーの初期値
ex=1E-4 #収束判定値
Th2n=Th20 #初期値の受け渡し
while error > ex:
Th2n1=Th2n-fTh2(Th2n)/dfTh2(Th2n) #(4)式
error=abs(Th2n1-Th2n) #error値計算
print(n,Th2n1,error) #計算回数、Th2、error値の出力
Th2n=Th2n1 #次のTh2値の受け渡し
n=n+1 #次のステップ2行目でnewton(Th20)という関数を定義し、4行目から収束計算式の条件を書いていきます。
4行目は収束計算回数をnという文字で定義します。初期値は1回目なのでn=1とします。
5行目はエラーの初期値を入力します。Newton-Raphson法の記事で解説していますがエラー値の計算は、
$$error=\left| Th2(n+1)-Th2(n)\right|・・・(3)$$
(3)式のようにn回目とn+1回目の計算値の絶対値を取ります。
このerror値が繰り返し計算でどんどん小さくなり、ほとんどゼロに近くなれば収束したとみなすことができます。
ただし最初の1回目は適当な値を初期値として設定する必要があり、今回はerror=1としています。
このerror値の初期値が小さすぎると最初から収束していると判定されかねないので、6行目の収束判定値と比較して十分大きい値を設定しましょう。
6行目に収束判定値を入力します。化学工学の分野では10-4くらいの精度があれば十分でしょう。
8行目で初期値の受け渡しを行なっています。Th2nをn回収束計算させた後のTh2の値とし、その初期値としてTh20=40℃としています。
10行目で繰り返し計算のメインとなるwhile文を入力しています。while文は後に入力する条件式がFalseになるまで:以降の実行文を繰り返す処理をします。
ここでの条件式は error > ex と入力しています。これはNewton-Raphson法の原理の通り、繰り返し計算のerror値が収束判定値exより大きければ繰り返し計算を続行することを意味しています。
この式がFalseになるということは error ≦ ex となる、つまりerror値が収束判定値ex以下になり収束したと判定できれば計算を終了します。
似たような計算はfor文でも行なうことができますが、for文では繰り返し計算回数をあらかじめ指定する必要があります。
今回の収束計算のように何回繰り返し計算するかわからない場合は、for文よりwhile文の方がコードを書きやすく向いていると思います。
11~17行目にwhile文の実行文を入力しています。実行文であることを示すために、必ずTabキーで字下げして入力位置を揃えるようにしましょう。
実行文の記述なのに字下げしていなかったり、文頭の位置が揃っていないとエラーになります。Pythonは特に字下げには厳しいです。
11行目にNewton-Raphson法のメインの収束計算式である(4)式を入力します。
$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}・・・(4)$$
fTh2やf'Th2の()内をTh2nと入力することで、定義した関数のTh2にTh2nの値を入力して計算させることができます。
12行目でn+1回目の計算値Th2n1とn回目の計算値Th2nの絶対値を取り、error値を算出しています。
14行目でprint関数を使用して計算回数n、計算値Th2、errorの値を出力しています。
この14行目はプログラミング言語特有の表現で、defで定義した関数の計算値を出力したい場合にはreturnやprintでわざわざ出力させる必要があります。
returnとprintの使い分けに関してはプログラミング言語特有の関数の考えを理解する必要があり、自分もなかなか理解が追い付いていないです。
とりあえず両方試してみてうまくいったprintの方を採用しています。この箇所をreturnにすると収束計算1回目の値しか出力されずうまくいきませんでした。
16行目で、11行目で計算したTh2n1の値を次のTh2nに受け渡す処理を行なっています。
これもプログラミング言語特有の表現で、今回のような繰り返し計算で変数を計算値によって更新し新たな計算をする場合にはよく使用される表現です。
今回は(4)式で計算させたTh2n1の値を新たなTh2nの値とし、もう一度(4)式に新たなTh2nの値を代入して計算する処理を行なっています。
17行目も同様に繰り返し計算回数の更新を行なっています。この式はnに1を足したものをnに代入して、nの値を更新させることを意味しています。
17行目の計算後はwhile文の冒頭に戻り、条件式がFalseになるまで同じ計算を繰り返します。
計算結果の出力
最後に計算した結果を出力します。
#計算結果の出力
newton(Th20) #関数newtonを出力このように記述することで、関数内で出力している計算回数n、計算値Th2、error値が出力されます。
計算結果の確認
特に入力ミス等がなければ計算が収束し結果が以下のように表示されます。
1 48.94924897942285 8.949248979422848
2 50.630925411891404 1.6816764324685565
3 50.66047021470539 0.029544802813987303
4 50.66047825986093 8.045155539093685e-06左から計算回数n、Th2、errorの順番で出力されていますが少し見づらいですね。
そんな場合には出力方法を少し工夫しましょう。
print(n,"\t",Th2n1,"\t",error) #計算回数、Th2、error値の出力while文のprintの入力で、各出力変数の間に"\t"を挟みます。これは水平タブと呼ばれ、水平方向の出力間隔を揃えるのに便利です。
この修正の後にもう一度計算すると、
1 48.94924897942285 8.949248979422848
2 50.630925411891404 1.6816764324685565
3 50.66047021470539 0.029544802813987303
4 50.66047825986093 8.045155539093685e-06上のような表示になります。ブログへの記入の都合上、でこぼこしているところがありますが、実際の出力画面はちゃんと文字同士の間隔が揃って見やすくなるはずです。
Excelで計算したこちらの記事の結果と同様に、4回で計算が収束しTh2=50.66℃となりました。きちんと計算できていますね。
下に計算コードを最初から最後までまとめて載せておきます。
#mathモジュールインポート
import math
#前提条件
F=45000 # kg/h
Cp=1 # kcal/(kg・℃)
U=550 # kcal/(m2・h・℃)
A=20 # m2
Th1=78 # ℃
Tc1=31 # ℃
Tc2=38 # ℃
#初期条件
Th20=40 # ℃
#その他計算条件
ΔT=0.001
#方程式定義
def fTh2(Th2):
return F*Cp*(Tc2-Tc1)-U*A*((Th1-Tc2)-(Th2-Tc1))/math.log((Th1-Tc2)/(Th2-Tc1)) #(1)式定義
def dfTh2(Th2):
return (fTh2(Th2+ΔT)-fTh2(Th2))/ΔT #(2)式定義
#Newton-Raphson法
def newton(Th20):
n=1 #計算回数初期値
error=1 #エラーの初期値
ex=1E-4 #収束判定値
Th2n=Th20 #初期値の受け渡し
while error > ex:
Th2n1=Th2n-fTh2(Th2n)/dfTh2(Th2n) #(4)式
error=abs(Th2n1-Th2n) #error値計算
print(n,"\t",Th2n1,"\t",error) #計算回数、Th2、error値の出力
Th2n=Th2n1 #次のTh2値の受け渡し
n=n+1 #次のステップ
#計算結果の出力
newton(Th20) #関数newtonを出力Scipyモジュールを使用した別解
PythonのモジュールにはNewton-Raphson法を簡単に計算できるものがあるようです。
今回はScipy(サイパイ)というモジュールを使用してみます。
#scipyモジュールインポート
from scipy.optimize import newton
#前提条件
F=45000 # kg/h
Cp=1 # kcal/(kg・℃)
U=550 # kcal/(m2・h・℃)
A=20 # m2
Th1=78 # ℃
Tc1=31 # ℃
Tc2=38 # ℃
#その他計算条件
ΔT=0.001
#方程式定義
def fTh2(Th2):
return F*Cp*(Tc2-Tc1)-U*A*((Th1-Tc2)-(Th2-Tc1))/math.log((Th1-Tc2)/(Th2-Tc1))
#scipyのNewton-Raphson法
newton(fTh2,40) # (計算する関数,初期値) 全体の記述を上に示します。
2行目でScipyのnewton法をインポートしています。
前提条件、その他計算条件の記述は変わりません。
大きく変わる点は
- fTh2の微分であるf'Th2を定義しなくてよい
- while文等の収束計算式を入力しなくてよい
以上の点です。自分で全て入力したケースと比較するとだいぶ楽ですね。
21行目でscipyのnewton計算式を入力しています。括弧内は計算する関数とTh2の初期値をそれぞれ入力します。
この記述でコードをRunさせると、
50.66047825978493このように収束したTh2の値が表示されます。
慣れてくればこのようなモジュールを使用してどんどん楽に計算することができます。
まとめ
Pythonで対数平均温度差を含む熱収支計算をNewton-Raphson法で計算する方法を解説しました。
非線形方程式の解法としてよく使用するのでぜひ覚えておきましょう。
